Wykłady z Matematyki.

Prowadzący: dr hab. Stanisław Stoiński

I Rok Chemii Semestr zimowy

Wykłady by „CHEMIA TEAM” w składzie:

1. Grzegorz „KHΦT” Florjańczyk

2. Arek „Arczi” Spychała

3. Michał „Szerlok” Wassel

4. Maciej „Starosta” Laskowski

5. Wojtek „Czajka I Wielki” Koziorowski

Całej braci studenckiej życzę miłej nauki i powodzenia na egzaminie!

Arczi

Rozdział I Zagadnienia wstępne

§ 1. Rachunek zdań.

Będziemy posługiwać się językiem, składającym się ze zdań, interesuje nas budowa logiczna zdania. Zdaniom przyporządkowujemy wartości logiczne: prawdę lub fałsz. Funkcją zdaniową nazywamy wyrażenie, które zawiera zmienną przyjmującą wartości z pewnego zakresu, przy czym podstawienie konkretnej wartości zmiennej prowadzi zawsze do zdania prawdziwego lub zdania fałszywego.

Np. wyrażenie f(p) da p X jest funkcją zdaniową jednej zmiennej. Funkcja zdaniowa może zależeć o wielu zmiennych np. f(p₁), ... f(p_n) gdzie p₁ X₁, ... p_n X_n jest funkcją zdaniową n zmiennych. Jeżeli zmienna funkcji zdaniowej przyjmuje wartości, które są zdaniami, to nazywamy ją zmienną zdaniową. Jeżeli p,q,r są zdaniami to przy pomocy tak zwanych punktorów zdaniotwórczych:

koniunkcji Λ („oraz”)

implikacji => („implikuje”)

alternatywie ! („lub”)

równoważności

można tworzyć zdania złożone. Jeżeli p,q,r... są zmiennymi zdaniowymi to przy pomocy punktorów zdaniotwórczych można utworzyć następujące funkcje zdaniowe.

Koniunkcje pΛg

Implikacje p => q

Alternatywę p∨q

Równoważność p q

Przykłady:

1. Niech

p = prosta l leży na płaszczyźnie a

q = punkt p leży na płaszczyźnie l

r = punkt p leży na płaszczyźnie a

Zdanie (pΛg)=>r jest zdaniem złożonym. Jest to zdanie prawdziwe.

2. Niech

p - liczba całkowita x podzielna przez 3

q - liczba całkowita x jest parzysta

r - liczba całkowita x jest podzielna przez 5

Funkcja zdania (pΛg)=>r dla xεC zbiór liczb całkowitych jest zdaniem prawdziwym np. dla x liczby całkowitej x=30. Dla pewnych xεC funkcja ta jest zdaniem fałszywym, np. dla x=6

Wartość logiczna „prawda” będziemy oznaczać cyfrą „1” Wartość logiczną fałsz będziemy oznaczać cyfrą „0”. Wartości logiczne funkcji zdaniowych :

A. koniunkcja pΛg

P/g	1	0
1	1	0
0	0	0

B. implikacja p=>q

P/g	1	0
1	1	0
0	1	1

C. alternatywa pVq

P/g	1	0
1	1	1
0	1	0

D. równoważność pq

P/g	1	0
1	1	0
0	0	1

Powyższe funktory zdaniotwórcze nazywamy funktorami dwuczłonowymi. Funktory jednoczłonowe to: potwierdzenie i negacja.

Potwierdzenie zdania p to zdanie p. Wartości logiczne negacji zdania p to znaczy zdania p'.

p	p'
1	0
0	1

Mówimy, że zdanie p jest warunkiem koniecznym dla zdania q, jeżeli q=>p. Zdanie p jest warunkiem dostatecznym dla zdania q, jeżeli p=>q.

Mówimy, że p jest warunkiem dostatecznym i koniecznym dla q, gdy prawdziwe jest zdanie (q=>p)i(p=>q) lub, równoważne pq.

Przykłady :

1. Niech

p = dwie proste w przestrzeni nie przecinają się

q = dwie proste w przestrzeni równoległe

Widać, że jeżeli q=>p oraz p=>q. Zatem nie przecinanie się prostych w przestrzeni jest warunkiem koniecznym, ale nie dostatecznym równoległości prostych w przestrzeni, gdyż tzw. Proste wichrowe nie są równoległe i nie przecinają się.

2. Niech

p = suma nieskończona liczb rzeczywistych (a₁, a₂, itd.)

jest liczbą rzeczywistą

q =

Wtedy można udowodnić, że

p=>q

(Warunek konieczny zbieżność szeregów)

oraz q=>p gdyż np.:

Ciekawostka

Funkcję zdaniową, która po podstawieniu w miejsce zmiennych zdań o dowolnej wartości logicznej jest zawsze zdaniem prawdziwym nazywamy tautologią.

Przykłady tautologii:

Prawo transpozycji

(q'=>p')(p=>q)

Prawo sylogizmy

[(p=>q) Λ(q=>r)]=>(p=>r)

Prawa de Morgana

(pΛq)'(p'Vq')

(pVq)' (p'Λq')

4. Zaprzeczenie implikacji

(p=>q)'(pΛq')

5. Równoważność

(pq)[(p=>q) Λ(q=>p)

Sprawdzenie czy dana funkcja zdaniowa jest tautologią dokonujemy stosują tak zwana metodę prób 0-jedynkwych. Polega ona na tym, że badamy wszystkie możliwe przypadki wartości logicznych zdań podstawianych w miejsce zmiennych.

Ćwiczenie: Sprawdzić czy funkcja zdaniowa pV(qΛr)(pVq) Λ(pVr) jest tautologią.

§ 2. Kwantyfikatory.

Niech p(x) będzie funkcją zdaniową zmiennej X z zakresem zmiennośc X. Kwantyfikatorem szczegółowym nazywamy słowo istnieje. Natomiast kwantyfikatorem ogólnym nazywamy słowa dla każdego. W dalszym ciągu kwantyfikator szczegółowy będziemy oznaczać ∃, natomiast kwantyfikator ogólny oznaczać symbolem ∀. Kwantyfikator szczegółowy oznaczamy też symbolem V a kwantyfikator ogólny symbolem Λ. Wyrażenia
są zdaniami.

Przykłady:

Zdanie
zdanie jest fałszywe.

Zdanie
jest zdaniem prawdziwym.

Jeżeli funkcja zdaniowa zależy od większej ilości zmiennych to, to zdanie budowane z niej przy pomocy kwantyfikatorów zawiera tyle kwantyfikatorów ile jest zmiennych (przykład Załóżmy, że zakres zmienności X składa się ze skończonej ilości elementów x₁, x₂, x_n. Wtedy dla funkcji zdaniowej p(x) otrzymujemy

Stąd :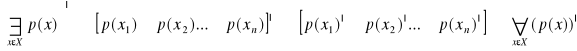

Podobnie otrzymujemy :

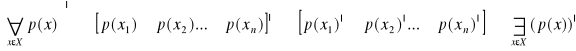
można udowodnić, że dla dowolnego zakresu zmienność X zachodzą prawa de Morgana.

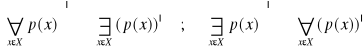
Zdanie, w którym kilka kwantyfikatorów poprzedza funkcję zdaniową negujemy zamieniając kwantyfikatory szczegółowe na ogólne, a ogólne na szczegółowe i negując funkcję zdaniową. Np.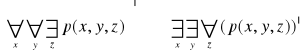

Kolejność kwantyfikatorów można zmieniać w następujących przypadkach:

Równoważność przy zmianie kolejności kwantyfikatora ogólnego i szczegółowego nie jest prawdziwa. Jest jednak słuszna implikacja:
. Dana funkcja zdaniowa ........ gdzie xεX W pewnych przypadkach budując ......p(x). Zdanie .... zawężamy zakres zmienności zmiennej zdaniowej x. Biorąc pod uwagę wartości c, dla których jest prawdziwe zdanie. Wtedy
;

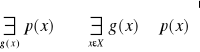
Kwantyfikatory
nazywamy kwantyfikatorami i ograniczonym zakresie.

Przykłady:

1. Zadanie: Ciąg liczb rzeczywistych (a_n) jest zbieżny do granicy gεR, zapisujemy następująco: dla dowolnie małej liczby dodatniej istnieje liczba dodatnia, taka, że dla każdego wskaźnika n>N zachodzi nierówność |a_n-q|<ε

|a_n-q| <ε -ε <a_n - g< ε ; ε-<a_n<g+ε

2. Ciąg (a_n) o wyrazach rzeczywistych gdy jego wyrazy stale rosną (maleją) nazywyamy monotonicznym. Zdanie ciag (a_n) jest monotoniczny zapisujemy następująco:

.

§ 3. Algebra zbiorów

Jako pojęcia pierwotne przyjmujemy zbiór, element zbioru, przynależność elementu do zbioru. Zdanie xε należy do zbioru A oznaczamy symbolem xεA

Ponadto
x nie należy do zbioru A.

Określamy:

Zawieranie, (inkluzja) zbioru A,B:
jeżeli A⊂C, to A jest podzbiorem B.

Zbiory identyczne A,B

;

Zbiór A, jest zawarty z sposób właściwy w B lub jest podzbiorem właściwym B. Zbiór pusty ∅ nazywamy zbiór który nie zawiera żadnego elementu. Ponieważ xε∅ => xεA, gdzie A jest osobnym zbiorem. Więc ∅ jest podzbiorem dowolnego zbioru. Zbiór pusty A nazywamy podzbiorami niewłaściwymi zbioru A. Oznaczamy przez W(x) własności elementu X; zbiór elementów posiadających własności W(x) oznaczamy symbolem
Np.:

1. Zbiór

2. Zbiór
liczb rzeczywistych niedodatnich.

Działania na zbiorach .

Suma zbioru A,B

Iloczyn zbiorów A,B

Jeżeli A∩B=∅, to znaczy zbiory A i B są rozłączne.

Różnica zbiorów:

Różnica symetryczna A\B

A-B=(A∪B)\(A∩B)

Zachodzą następujące prawa algebry zbiorów:

prawa de Morgana

A\(B∪C)=(A\B) ∩(A\C)

A\(B∩C)=(A\B) ∪(A\C)

przemienności

A∪B=B∪A A∩B=B∩A

łączności

A∪(B∪C)=(A∪B) ∪C

A∩(B∩C)=(A∩B) ∩C

rozdzielności

A∩(B∪C)=(A∩B) ∪(A∩C)

A∪(B∩C)=(A∪B) ∩ (A∪C)

Dla liczb rzeczywistych a,b,c należących do R zachodzi równość:

a*(b+c)=a*b+a*c

a+b*c=(a+b)*(a+c)

Jeżeli ograniczymy się do rozpatrywania podzbioru danego zbioru X to przy aεX piszemy

Wtedy zbiór A' nazywamy dopełnieniem zbioru A.

Prawa de Morgana dla dopełnień mają postać.

Iloczynem kartezjańskim lub produktem kartezjańskim zbiorów A,B nazywamy zbiór, który będziemy oznaczać przez AXB par uporządkowanych A,B takich, że aεA, bεB tzn. AXB={(a,b): aεA, bεB}

Np. Jeżeli A=B=(-∞;∞) to AXB jest zbiorem punktów płaszczyzny. Można rozważać iloczyn kartezjański w skończonej ilości zbiorów A₁, A_x, A_n przyjmując

A_aXA₂X.........XA_n={a₁, a₂, ….a_n εA_n; a₁εA₁; … a_nεA_n}

§ 4. Relacje i funkcje

1. Relacje

Relacją R między elementami zbioru A,B nazywamy podzbiór iloczynu kartezjańskiego AXB.

Mówimy, że xεA, oraz yεB pozostają względem siebie w relacji R, co zapisujemy xRy jeżeli para x,y należy do podzbioru R, tzn.: R={(x,y) ε A i B: xRy}

Relacja nierówności xRy x≥y w zbiorze ≡ iloczynie kartezjańskim (-∞;∞)X(-∞;∞)

Relacje xRy x²+y²­­≤a² a>0 to zbiór punktów koła wraz z okręgiem x²+y²­­=a², o środku (0,0) i promieniu a

Relację xRy nazywamy porządkującą jeżeli zachodzą następujące 4 warunki :

Relacja ≤ w zbiorze (-∞;∞)X(-∞;∞) jest relacją porządkującą w zbiorze liczb rzeczywistych. Relację porządkującą w zbiorze liczb rzeczywistych oznaczamy symbolem

Zbiór, w którym określona jest relacją porządkująca nazywamy zbiorem uporządkowanym. To znaczy np. zbiór R z relacją ≥ jest uporządkowany. Relację R: zwrotną, przechodnią oraz słabo symetryczną nazywamy częściowo porządkującą, oznaczamy ją również symbolem

Przykład: Oznaczmy zbiór wszystkich podzbiorów zbioru niepustego X zbiorem tym określamy relację. Jeżeli (AεX i BεX) => (A B A⊂B). Ponieważ:

1. A⊂A

2. jeżeli A⊂B ∧ B⊂C => A⊂C

3. A⊂C ∧ B⊂A => A=B

Jest to relacja częściowo porządkująca. Dla zbioru A,B⊂X rozłącznych to znaczy takich, że A∩B=∅ nie zachodzi spójność :

1. Funkcje

Relację f między elementami zbiorów X,Y nazywamy funkcją określoną na zbiorze X i wartościach ze zbioru Y jeżeli: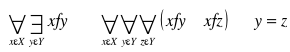
Wtedy funkcję f odwzorowuje zbiór X w zbiór Y co zapisujemy następująco fx->Y lub Y=f(x) dla xεX. Zbiór X nazywamy wówczas dziedziną funkcji f, a zbiór Y={yεY: y=f(x) dla xεX} nazywamy przeciwdziedziną funkcji f. Jeżeli Y₀=Y to wtedy fX=Y jest suriekcją X na Y. Relację f nazywamy funkcją odwzorowującą zbiór X w zbiór Y lub funkcja wzajemnie jednoznaczną albo iniekcją. Jeżeli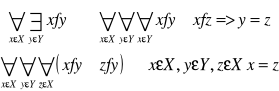

Przykłady:

1. Funkcja y=sinx, y=cosx dla xε(-∞;∞) nie są wzajemnie jednoznaczne.

2. Funkcje (x,y)=(rcosϕ, rsinϕ, 0≤ϕ≤2π, 0≤r≤1 odwzorowuje punkty prostokąta. X=<0, 2π>X<0,1> na zbiór punkty koła Y={(rcosϕ, rsinϕ) : yε<0, 2π>, rε<0,1>

x²+y²=r²cos²ϕ+ r²sin²ϕ=r²(cos²ϕ+sin²ϕ)=r²

Określona w ten sposób funkcja nie jest wzajemnie jednoznaczna gdyż środek koła Y oznacza punkt (0,0) odpowiada bokowi prostokąta X określonej następująco: Y r=0, ϕε<0,2>.

3. Każda funkcja rzeczywista zmiennej rzeczywistej rosnąca lub malejąca jest funkcją wzajemnie jednoznaczną np. funkcja liniowa y=ax+b a≠0 jest funkcją wzajemnie jednoznaczną. Funkcja f odwzorowuje zbiór X na zbiorze Y jeżeli dla każdego
jeżeli nie zakładamy powyższego f odwzorowuje X w zbiór Y. Jeżeli funkcja fzX do Y jest jednocześnie iniekcją oraz surekcją, to mówimy, że f jest bijekcją zbiorów X i Y. Funkcją odwzorowującą wzajemnie jednoznaczną X na Y tzn. bijekcją, wyznacza również xεX jako funkcję yεY otrzymaną w ten sposób oznaczamy przez f_-1 i nazywamy funkcją odwrotną do f. Zatem wtedy zachodzi nierówność yf_-1xxfy:

Przykłady:

1. Funkcję odwrotną do funkcji y=x³ dla xε(-∞;∞) jest funkcja
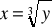
   dla yε(-∞;∞)

2. Funkcję odwrotną do funkcji liniowej y=ax+b, a≠0 jest funkcja liczbowa
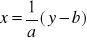
   . Niech funkcja odwzorowuje X na Y oraz niech A⊂X, B⊂Y. Obrazem zbioru A nazywamy zbiór : f(A)={y:yεY ∧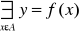
   }

Przeciwobrazem zbioru B nazywamy zbiór B nazywamy zbiór f_-1(B)={x:xεX∧
}

Własności obrazów i przeciwobrazów:

1. obraz sumy : f(A₁∪A₂) = f(A₁)∪f(A₂)

2. obraz przekroju : f(A₁∩A₂) ⊂ f(A₁) ∩ f(A₂)

3. f_-1(B₁∪B₂) = f_-1(B₁)∪ f_-1(B₂)

4. f_-1 (B₁∩B₂) = f_-1 (B₁) ∩ f_-1 (B₂)

Funkcje ograniczone, monotoniczne i wypukłe.

Funkcję f:x->R, gdzie R= xε(-∞;∞), zbiór liczb rzeczywistych, nazywamy ograniczoną gdy jej przeciwdziedzina f(x) jest zbiorem ograniczonym.

Analogicznie określone funkcje ograniczone z góry lub z dołu np. Mówimy, że f:x->R jest ograniczona z dołu jeżeli:

Przykłady:

1. Funkcje

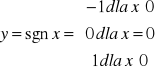
2. Funkcja

jest ograniczona z góry dla xၥ(-Ⴅ;0) oraz ograniczona z dołu dla xၥ(0;Ⴅ)

Niech f:x->Y gdzie X,Y ⊂R. Mówimy, że :

1. f jest rosnąca na , jeżeli
   

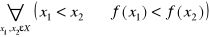
2. f jest malejąca na X jeżeli :
   

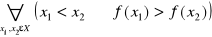
3. f jest niemalejąca na X jeżeli :
   

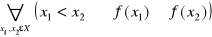
4. f jest nierosnąca na X jeżeli:
   

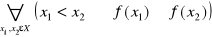
Funkcje typu 1-4 nazywamy monotonicznymi. Natomiast funkcje rosnące i malejące funkcjami ................. . Funkcje f odwzorowującą przedział x⊂R w zbiór Y⊂R nazywamy wypukła jeżeli:
. Funkcję odwzorowującą przedział x⊂R w zbiór Y⊂R nazywamy wklęsłą jeżeli :
.

4.2 Funkcje elementarne

Przyjmujemy następujące oznaczenia: R=(-∞,∞) - zbiór liczb rzeczywistych.

(a,b)={zbiór tych xεR a<x<b} przedział otwarty.

<a,b>={xεR a≤x≤b} przedział domknięty.

Funkcja stała

Funkcję f określoną na zbiorze X⊂R o wartościach ze R nazywamy stałą gdy :

Funkcja schodkowa.

Niech a=x₀≤x₁≤x₂≤...≤x_n-1≤x_n-2

Jeżeli f jest funkcją stałą w każdym przedziale. [X_i-1,X_i] i=1,2,....,n to f nazywamy funkcją schodkową /Uwaga: Nawias [ ] oznacza, że punkty X_i-1,X_i mogą należeć do przedziału lub leża poza nim.

Niech f(x)=C_i dla xε[ X_i-1,X_i ] i=1,2,...,n

Wielomian.

Funkcję f określoną równością f(x)=a₀xⁿ+a₁x^n-1+a₂x^n-2+...+a_nx gdzie n jest liczbą R₊ a,a₁,..a_nεR a≠0 nazywamy wielomian stopnia n (wielomian algebraiczny). Jest to funkcja określona dla każdego xεR.

Funkcja wymierna.

Funkcja f, która jest ilorazem dwóch wielomianów, nazywa się funkcją wymierną. Jeżeli

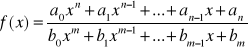
. Jeżeli funkcja jest określona w zbiorze R z pominięciem miejsc zerowych mianownika, przy założeniu, że licznik i mianownik nie posiadają wspólnych pierwiastków. W szczególności funkcja
nazywa się funkcją homograficzną i jest określona na zbiorze X=R\{0,
}

Funkcja potęgowa

Funkcję f określoną równością f(x)=x^α gdzie α - dowolna liczba rzeczywista, nazywamy funkcją potęgową.

Jeżeli α=n, n - liczb naturalna, to
dla każdego xεX=R

Jeżeli α=0, to
dla xεR\{0}

Jeżeli ၡ=-n, n - liczba naturalna to
dla xεR\{0}

Jeżeli ၡ=
n - liczba naturalna (pierwiastek n-tego stopnia)

Dla xၥX=R gdy n jest liczbą nieparzystą, oraz dla xၥX=<0; ∞), gdy n jest liczbą parzystą.

Jeżeli ၡ=
; m - liczba całkowita, n - liczba naturalna to
definiujemy
.

Jest prawdziwe następujące: Twierdzenie 1.

Jeżeli x≥0, ၡ jest liczbą rzeczywistą, (w_n) (v_n) są ciągami liczb wymiernych zbieżnymi do ၡ, to ciągi potęg
są zbieżne oraz granice tych ciągów

Definicja potęgi o wykładniku rzeczywistym.

Jeżeli x≥0, α- jest liczbą rzeczywistą, to
gdzie (W_n) jest ciągiem liczb wymiernych zbieżnych do a. Przy x=0 zakładamy, że α>0.

Z twierdzenia 1 wynika, że granica
:

• Istnieje

• Jest skończona i dodatnia, gdy X>0, oraz nie zależy od wyrazy ciągu liczb wymiernych W_n zbieżnego do α .

Dla x,x₁,x₂>0 oraz dla α,β εR zachodzą równości:

• 
  

• 
  

• 
  

• 
  

• 
  

4

5

---