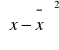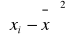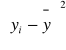STATYSTYKA

Literatura podstawowa:

1. Wacława Starzyńska - „Statystyka praktyczna”; PWN 2002, 2004

2. Gorg A. Ferguson, Yosho Takana - Analiza Statystyczna w psychologii i pedagogice”; PWN

3. Jarosław Podgórski - „ Statystyka dla studiów licencjackich”; PWE

Literatura uzupełniająca:

1. Jerzy Brzeziński - „Metodologia badań psychologicznych”; PWN

2. Chawa Frankword-Nachmias, David Nachmias - „Metody badawcze w naukach społecznych”; Zysk i Sp.

1. PODSTAWOWE POJĘCIA STATYSTYKI 01.10.2006

Statystyka inaczej:

• zestawienie faktów, liczb i zdarzeń

• miara rozkładu zmiennej zbiorowości

• pewna dyscyplina nauki - jest to nauka zajmująca się metodami badań obiektów i zdarzeń w ich masowych przejawach oraz ich ilościową lub jakościową analizą (zajmuje się obiektami w sensie masowym)

Statystyka dzieli się na dwa działy:

1. Statystyka opisowa - zajmuje się zbiorowością, wyznaczeniem miar statystycznych oraz prezentację danych

2. Statystyka indukcyjna - inaczej matematyczna - zajmuje się określeniem właściwości populacji na podstawie zredukowanej liczby informacji (na podstawie próby) przy użyciu metod opartych na rachunku prawdopodobieństwa

Rodzaje zbiorowości:

1. zbiorowość generalna, inaczej populacja - jest to zbiór wszystkich obiektów lub zdarzeń poddanych badaniu statystycznemu, co do których formułujemy wnioski natury ogólnej, na podstawie zredukowanej liczby informacji

2. Zbiorowość próbna - jest to podzbiór zbiorowości generalnej, wybrany w określony sposób i poddany obserwacji statystycznej

Elementy zbiorowości to JEDNOSTKI STATYSTYCZNE

Jednostki statystyczne - posiadają pewne właściwości

- właściwości istotne z punktu widzenia badania, nazywamy CECHAMI STATYSTYCZNYMI

TYPOLOGIA CECH STATYSTYCZNYCH

Cechy stałe - są to właściwości, takie same dla wszystkich badanych jednostek, zbiorowości

- służą do opisu zbiorowości

• c. rzeczowe - kogo? lub co? badamy

• c. czasowe - jakiego momentu lub okresu czasu dotyczy badanie

• c. terytorialne - gdzie znajduje się lub skąd pochodzi badana zbiorowość

Cechy zmienne (zmienne) - są to właściwości, które różnicują badane zbiorowości

A. Zmienne jakościowe - to niemierzalne

- opisuje się w sposób symboliczny lub opisowy

- posiadają swoje warianty

• z. nominalne - mogą zachodzić warianty: „=” lub „≠” , np. płeć

• z. porządkowe - może mieć warianty „=”, „≠” oraz dodatkowo relacja porządkowa „<”, „>” , np. zadowolenie z produktu

B. Zmienne ilościowe - to mierzalne

- przedstawia się w postaci liczbowej

- posiadają swoje wartości

• z. interwałowe (podziałowa) - ta zmienna posiada arbitralnie określony punkt zerowy

[arbitralny punkt - to punkt zerowy określony przez człowieka]

• z. ilorazowe (stosunkowa) -posiada naturalny punkt zerowy

[naturalny punkt zerowy - to określony przez naturę, np. waga]

zmienne ilościowe jako całość dzielimy na:

• z. ciągłe - może przyjmować naturalne wartości z określonego przedziału liczbowego

[np. wzrost od 160-170 zawsze można znaleźć wartość pośrodku, np. 160-161, może być 160,5]

• z. nieciągłe (dyskretna)- - ta przyjmuje wartości, które zmieniają się skokowo, czyli bez wartości pośrednich

PORZĄDKOWANIE I GRUPOWANIE DANYCH

1. PORZĄDKOWANIE - zmiennej ilościowej polega na utworzeniu rosnącego lub malejącego ciągu jej wartości

2. GRUPOWANIE - polega na przyporządkowaniu jednostek zbiorowości do określonych podgrup tej zbiorowości, zwanych klasami utworzonych ze względu na wartość zmiennej.

Uporządkowane i pogrupowane dane przedstawia się najczęściej w formie szeregów statystycznych.

Rodzaje szeregów statystycznych:

• szczegółowy

• punktowy

• przedziałowy

np. zarobki

1) szereg szczegółowy

800, 800, 900, 1100, 1200

1600, 2100, 2100, 2100, 2700

2) szereg punktowy

xi	ni (fi)
800	2
900	1
1100	1
1200	1
1600	1
2200	3
2700	1
	N=10

x_i - x z indeksem „_i” - wskazuje na kolejną wartość, np. 1,2 i 3

x_i - to wartości zmiennej

n_i - liczebność jednostkowa, to liczba jednostek zbiorowości posiadających daną wartość zmiennej (fi)

N - liczebność zbiorowości (liczba jednostek badanej zbiorowości) N = n_i

- suma liczebności (częstotliwość)= liczebność zbiorowości

3) szereg przedziałowy

xi	ni
0-1000	3
1000-2000	3
2000-3000	4
	N=10

k - to liczba przedziałów w szeregu (k=3)

x_0i - to wartości, które rozpoczynają każdy przedział, to dolna granica przedziału

x_1i - wartości, które zamykają, to górna granica przedziału

- wartości, które są w środku przedziału, to środek przedziału, to średnia arytmetyczna górnej i dolnej granicy

h - rozpiętość lub szerokość przedziału (różnica między górną i dolną granicą)

R - rozstęp lub obszar zmienności

R= x _max - x_min

1. MIARY TENDENCJI CENTRALNEJ 15.10.2006

Wyróżniamy 3 miary:

1. Średnie

Średnia arytmetyczna:

• obliczana na podstawie wszystkich danych szeregu,

• na jej wartość duży wpływ mają wielkości skrajne,

• nadaje się do przekształceń algebraicznych,

• suma odchyleń od średniej równa się zeru (0)

2. Mediany

• nie mają na nią wpływu wartości skrajne,

• stosuje się głównie dla szeregów skrajnie asymetrycznych.

3. Dominanty (wartość modalna)

• jest wartością najbardziej typową dla szeregu,

• łatwo ją wyznaczyć z uporządkowanego szeregu prostego,

• dla szeregu rozdzielczego można ją tylko oszacować,

• przy małej liczebności może nie być dominanty, a przy dużej może wystąpić więcej niż jedna dominanta (przy dwóch dominantach szereg nazywamy bimodalnym).

Tendencja centralna:

ŚREDNIA ARYTMETYCZNA:

• dla szeregu szczegółowego

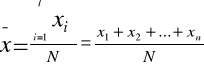
• dla szeregu punktowego

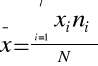
• dla szeregu przedziałowego

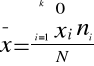
MEDIANA

Jest to wartość środkowa, która dzieli badaną zbiorowość na dwie równe części, takie, że jednostki pierwszej części posiadają wartości zmiennej nie większe od wartości mediany (= lub <), a jednostki drugiej części posiadają wartości nie mniejsze od wartości mediany (= lub >)

Przykład:

1,2,3,4,5 3 - to mediana

1,2,3,.., 4,5,6 3,5 - to mediana

1,1,1,1,2,3,7 1 - to mediana

• dla szeregu przedziałowego

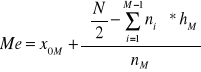
Me - mediana

x_0m - dolna granica przedziału mediany (_{0-to zero})

N - pozycja mediany

2

_M-1 - do przedziału poprzedniego

h_M - rozpiętość przedziału mediany

n_M - liczebność przedziału mediany

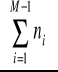
- to suma liczebności cząstkowych, liczona od początku szeregu do przedziału poprzedzającego przedział mediany

Szukanie przedziału pozycji mediany:

xi	ni (fi)	N 2	nisk
0-10	2	7	2
10-20	3	7	5 (2+3=5)
20-30	4	7	9 (5+4=9)
30-40	3	7	12
40-50	2	7	14
	N=14

n_isk - liczebność skumulowana dla danego przedziału jest sumą liczebności cząstkowych tegoż przedziału i wszystkich przedziałów go poprzedzających

liczba 9 - w tym miejscu przekroczyło nam liczbę 7 (pozycję mediany) i wówczas ten przedział jest przedziałem mediany

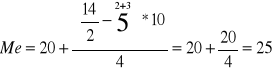
DOMINANTA

Dominanta - inaczej wartość typowa bądź modalna

- jest to wartość zmiennej, która powtarza się najczęściej w badanej zbiorowości

Sposób wyznaczania dominanty dla szeregu prostego

1. uporządkować szereg rosnąco (czasami malejąco),

2. podsumować jednostki, które maja tę samą wartość.

3. dominantą będzie wartość występująca najczęściej.

Sposób wyznaczania dominanty dla szeregu rozdzielczego

Dominantę z szeregu rozdzielczego można w przybliżeniu wyznaczyć także w sposób graficzny

gdzie: x_0D - dolna granica przedziału w którym znajduje się dominanta,

n_D - liczebność przedziału, w którym znajduje się dominanta,

n_D-1 - liczebność przedziału poprzedzającego przedział dominanty,

n_D+1 - liczebność przedziału następującego po przedziale dominanty

h_D - rozpiętość przedziału dominanty

- przedział dominanty - zawsze tam, gdzie jest największa liczebność

Przykład:

xi	ni (fi)	N 2	nisk
0-10	2	7	2
10-20	3 (2+3=5)	7	5
20-30	4 (5+4=9)	7	9
30-40	3 (9+3=12)	7	12
40-50	2 (12+2=14)	7	14
	N=14

ZADANIE 1:

Zbadano zatrudnienie w 40 najmniejszych firmach w Z.G. Uzyskano następujące wyniki:

xi	ni		ni
0-5	8	2,5	20
5-10	12	7,5	90
10-15	14	12,5	175
15-20	3	17,5	52,5
20-25	2	22,5	45
25-30	1	27,5	27,5
	N=40		410

Obliczyć średnią zatrudnienia dla firm

Obliczyć medianę i dominantę

Średnia:

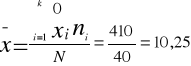
Mediana:

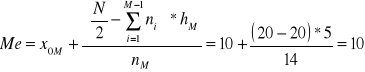
Dominanta:

ZADANIE 2:

Pewien student uzyskał na koniec III semestru następujące wyniki zaliczeń i egzaminów:

• Podstawy turystyki 3,0

• Informatyka 3,5

• Ekonomika turystyczna 5,0

• Statystyka 4,5

• J. angielski 3,0

• J. hiszpański 3,5

Student stara się o stypendium, które przysługuje od średniej 4,0. Czy student dostanie stypendium?

- średnia - szereg szczegółowy

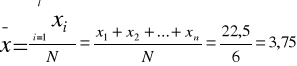
ZADANIE 3:

W obiektach turystycznych zachodniej Polski ustalono liczbę miejsc noclegowych, uzyskano następujące dane (wyniki)

xi	ni		ni
20-35	6	27,5	165
35-50	7	42,5	297,5
50-65	9	57,5	517,5
65-80	14	72,5	1015
80-95	7	87,5	612,5
95-110	3	102,5	307,5
110-125	2	117,5	235
	N=48		3150

Proszę określić średnią liczbę m-c noclegowych, przypadających na jeden obiekt w zachodniej Polsce.

Średnia - szereg przedziałowy

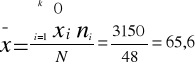
1. MIARY TENDENCJI CENTRALNEJ - MIARY POŁOŻENIA I KWARTYLI 05.11.2006

Q₁ = kwartyl 1

Q₂ = Me

Q₃ = kwartyl 3

• Kwartyl 1 - Q₁ to taka wartość zmiennej, która dzieli badaną zbiorowość w ten sposób, że ¼ jednostek zbiorowości posiada wartość zmiennej nie większe niż wartość kwartyna pierwszego, a ¾ jednostek zbiorowości posiada wartości nie mniejsze niż wartość kwartyna pierwszego.

(Q₁ dzieli zbiorowość na dwie części w sposób następujący - 25% jednostek statystycznych jeszcze tej wartości nie osiągnęło, a pozostałe 75% tę wartość przekroczyło.

• Kwartyl 2 - Q₂ - Me (mediana) to taka wartość badanej cechy, która dzieli populację na połowy, inaczej mówiąc jest to wartość środkowa. W medianie połowa populacji jeszcze nie osiągnęła wartości badanej cechy a druga połowa już tę wartość przekroczyła.

• Kwartyl 3 - Q₃ to taka wartość zmiennej, która dzieli badaną zbiorowość w ten sposób, że ¾ jednostek zbiorowości posiada wartość zmiennej nie większe niż wartość kwartyna trzeciego, a ¼ jednostek zbiorowości posiada wartości nie mniejsze niż wartość kwartyna trzeciego.

(Q₃ to taka wartość badanej cechy, której 75% liczebności jeszcze nie osiągnęło tej wielkości, a 25% ją przekroczyło)

Liczenie:

• określa się pozycję

• określa się, w którym przedziale

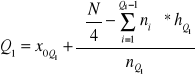
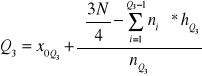
- dolna granica przedziału Q₁ lub Q₃

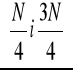
- pozycje Q₁ lub Q₃

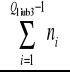
- suma liczebności cząstkowych liczona od początku szeregu (od góry) do przedziału poprzedzającego przedział Q₁ lub Q₃

- rozpiętość przedziału Q₁ lub Q₃

- liczebność przedziału Q₁ lub Q₃

ZADANIE:

Aby przyjąć do pracy nocnych urzędników Ministerstwo Gospodarki rozpisało konkurs, do konkursu zgłosiło się 100 kandydatów, ich prace i dorobek były punktowane od 0-16 punktów, do pracy w Ministerstwie można przyjąć 25 osób, które najlepiej wypadły w konkursie. Ile punktów należało uzyskać, żeby zdobyć pracę w Ministerstwie.

xi	ni	nisk	¾ N= ¾ *100 = 75
0-2	5	5	75
2-4	5	10	75
4-6	6	16	75
6-8	30	46	75
8-10	25	71	75
10-12	15	86	75
12-14	10	96	75
14-16	4	100	75
	N=100		3150

Uczestników było 100, chcą przyjąć 25, czyli ¼ - liczymy więc Q₃

(jeżeli 100, a ¼ najgorszych należy oddać na douczanie to liczymy Q₁)

Odp. Należy otrzymać min 10,53 punktów.

1. MIARY ZMIENNOŚCI - ZRÓŻNICOWANIA I DYSPERSJI

Miary zróżnicowania, to wartości, które uogólniają zróżnicowanie jednostek zbiorowości w postaci jednej miary (wartości)

1. rozstęp - oparta jest na wartościach skrajnych

R = x_max - x_min

Np. 20, 23 R= 3

20, 55 R= 35 - zmienność większa

2. odchylenie przeciętne

3. wariancja - to kwadrat średnich odchyleń wartości zmiennej od jej średniej arytmetycznej

(VAR;
-to parametry dla populacji, dla próby)

• dla szeregu szczegółowego

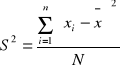
• dla szeregu punktowego

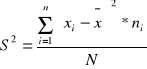
• dla szeregu przedziałowego

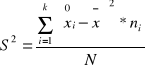
Jeśli S² jest większe, to tam zróżnicowanie zbiorowości jest większe.

4. odchylenie standardowe - jako miara zmienności wskazuje na to o ile średnio odchylają się wartości zmiennej w badanej zbiorowości od średniej arytmetycznej.

(im jest większe odchylenie, tym zróżnicowanie większe)

Np. S=200 i S=500 -tu jest większa zmienność

WAŻNE! - żeby porównywać muszą być takie same średnie

5. współczynniki zmienności (V_S) - to miara, która umożliwia porównanie zmienności w różnych zbiorowościach, gdy średnie arytmetyczne w tych zbiorowościach nie są takie same.

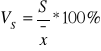
- z reguły wyrażany w procentach

6. klasyczny i kwartylowy obszar zmienności

ZADANIE:

Dane dotyczą całego roku 2005.

Zbadano ceny biletów z Warszawy do Londynu w dwóch tanich firmach A iB.

Uzyskano następujące miary dot. firmy A, średnia cena biletów 400 zł, a odchylenie standardowe70.

W firmie B szereg szczegółowy w zł.

Należy ustalić, w której firmie A czy B nastąpiło większe zróżnicowanie cen biletów.

Firma A:

S = 70

śr. arytm. = 400

- to 17,5 punktów procentowych

Firma B: 12 miesięcy

xi	ni
225	1	300	-75	5 625
225	1	300	-75	5 625
230	1	300	-70	4 900
236	1	300	-64	4 096
270	1	300	-30	900
382	1	300	82	6 724
322	1	300	22	484
324	1	300	24	576
320	1	300	20	400
310	1	300	10	100
368	1	300	68	4 624
388	1	300	88	7 744
3600				41798

= 3600:12 =300

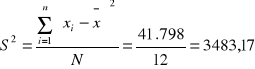
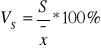
Odp. Firma B ma większe zróżnicowanie o 2,2 punkty procentowe

1. ANALIZA KORELACJI I REGRESJI 03.12.2006 R

Regresja - oznacza wpływ zmiennej traktowanej jako niezależna (skutek) na zmianę traktowaną jako zależną (przyczyna)

Korelacja - jest to współzależność zmiennych i nie istnieje tu potrzeba rozstrzygania, która ze zmiennych jest przyczyną, a która skutkiem.

zgromadzenie danych

xi	yi
1	2
2	4
3	6
4	8
5	10
6	12

Wykres- diagram rozrzutu - to wykres punktowy:

1 2 3 4 5 6

O istnieniu związku korelacyjnego między zmiennymi można wnioskować na podstawie wykresów rozrzutu (diagramów rozrzutu lub diagramów korelacyjnych) oraz przy pomocy miar statystycznych.

Najprostsze miary korelacji to współczynniki korelacji:

1. współczynnik korelacji PEARSONA - używa się do ustalania związku korelacyjnego pomiędzy zmiennymi ilościowymi

2. współczynnik korelacji SPEARMANA - używa się do ustalania związku korelacyjnego pomiędzy zmiennymi porządkowymi, porządkowo-ilościowymi lub ilościowymi.

PEARSON:

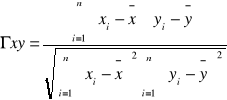
KIERUNEK KORELACJI:

Korelacja jest zgodna (dodatnia) wtedy, kiedy wartości jednej zmiennej zmieniają się w tym samym kierunku co wartości drugiej zmiennej

Korelacja jest niezgodna (ujemna) wtedy, kiedy wartości jednej zmiennej zmieniają się w przeciwnym kierunku co do wartości drugiej zmiennej (np. jedna rośnie, a druga maleje

INTERPRETACJA WYNIKÓW:

Współczynnik korelacji przyjmuje wartości z przedziału od -1 do +1.

Jego znak informuje o kierunku korelacji, a jego wartość bezwzględna informuje o sile korelacji.

SIŁA KORELACJI:

0 -0,2 -istnieje korelacja, ale nieznaczna

0,2 -0,4 -korelacja niska, słaba

0,4 -0,6 -korelacja umiarkowana

0,6 -0,8 -korelacja silna, znacząca

0,8 -0,99 -korelacja bardzo silna

1 -korelacja doskonała

SPEARMAN (współczynnik korelacji RANG - oparty na rangach)

Wartości zmiennej liczbowej uporządkowane:

2,3,7,9,9,9,10 9,9,9 - liczby powtarzające się to liczby związane -

Rangi 1 2 3 4 5 6 7 wszystkie otrzymają rangę 5, ponieważ

1 2 3 5 5 5 7 4+5+6=15 a 15: 3=5

Ranga - dla uporządkowanych wartości zmiennej jest numerem jej miejsca w tymże uporządkowanym szeregu.

Ranga dla liczb związanych jest średnią arytmetyczną jej numerów w szeregu.

Wartości zmiennej porządkowej:

Np. wykształcenie - zmienna porządkowa, nie można przedstawić liczbowo

podstawowe, podstawowe, średnie, średnie, średnie, wyższe, wyższe

1 2 3 4 5 6 7

Rangi 1,5 1,5 4 4 4 6,5 6,5

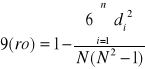
d_i - różnice rang d_i = Rx_i - Ry_i

INTERPRETACJA WYNIKÓW taka sama jak u PEARSONA

ZADANIE 1

Zyski teatrów zależą w pewnej mierze od ilości premier w sezonie. Należy zbadać, czy pomiędzy tymi dwoma zmiennymi istnieje związek korelacyjny, jaki jest jego kierunek oraz siła (zbadano 7 teatrów)

xi liczba premier	yi zysk w tys.
1	85	-2	-25	4	625	50
3	105	0	-5	0	25	0
2	100	-1	-10	1	100	10
3	110	0	0	0	0	0
4	125	1	15	1	225	15
3	115	0	5	0	25	0
5	130	2	20	4	400	40
21	770			10	1400	115

Średnia arytmetyczna x = 21 : 7 =3

Średnia arytmetyczna y = 770 : 7 =110

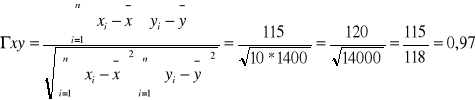
Odp. Korelacja jest dodatnia i bardzo silna.

ZADANIE 2:

Zbadać zależność pomiędzy czasem przeznaczonym na reklamę telewizorów pewnej marki, a ich miesięczną sprzedaż.

Dane ilustrują nam czas w mediach na reklamę w minutach, oraz liczbę sprzedanych telewizorów w tys. w okresie 7 m-cy.

x- czas na reklamę

y - sprzedaż telewizorów

xi	rangi	yi	rangi	di	di^2
10	2	2,5	2	0	0
18	6	4,6	5	1	1
13	3	5,2	6	-3	9
14	4	4,0	4	0	0
20	7	5,6	7	0	0
15	5	3,2	3	2	4
8	1	1,5	1	0	0
					14

xi	rangi	yi	rangi
8	1	1,5	1
10	2	2,5	2
13	3	3,2	3
14	4	4,0	4
15	5	4,6	5
18	6	5,2	6
20	7	5,6	7

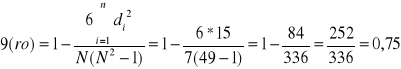
Odp. Korelacja bardzo silna.

1

CECHU STATYSTYCZNE

Cechy stałe

Cechy zmienne (zmienne)

- c. rzeczowe

- c. czasowe

- c. terytorialne

c. jakościowe

c. ilościowe

-c. nominalne

-c. porządkowe

- c. interwałowe

- c. ilorazowe

c. ciągłe

c. nieciągłe

wartość rzeczywiste

Dominanta rzeczywiste

Wartość zmiennej

Liczebność (częstość występowania

Obszar pomiędzy to tendencja centralna

n

x

Dominanta

wartość rzeczywiste

Dominanta rzeczywiste

Wartość badanej cechy (cecha mierzalna

Liczebność (% lub liczby rzeczywiste

wartość rzeczywiste

Wartość zmiennej

Liczebność

Q₁

Q₂

Q₃

8

6

4

2

4

Korelacja dodatnia

Korelacja ujemna

x

x

y

y

y

y

---