Zakład Inżynierii Wodnej Warszawa, dnia 19.09.2007 r.
Katedra Inżynierii Wodnej i Rekultywacji Środowiska
Wydział Inżynierii i Kształtowania Środowiska
SGGW
Projekt upustu stokowego
Katarzyna Anusiewicz
Budownictwo, rok I mgr
grupa II
Części składowe projektu upustu stokowego:
1 Opis techniczny
Wybór lokalizacji zapory i trasy bystrza
Warunki posadowienia: geologiczne, topograficzne
Opis zaprojektowanej konstrukcji
Eksploatacja i obsługa upustu
1.5 Technologia robót
wykonawczych
1.6 Przeprowadzenie wody w okresie budowy
Określenie rzędnej korony zapory
Obliczenia hydrauliczne
3.1 Wlotu
3.1.1 Dobór wymiarów
3.1.2 Obliczenie układu zwierciadła wody
3.1.3 Krzywa wydatku
3.2Bystrza
Strumień nie napowietrzony
Strumień napowietrzony
3.3 Urządzeń do rozpraszania energii
Określenie położenia wysokościowego wypadu
Obliczenie długości wypadu
Dobór kształtu i wymiarów wypadu.
4 Dobór umocnień i obliczenie rozmyć poniżej upustu.
Długość i rodzaj umocnień kanału doprowadzającego.
Długość i rodzaj umocnień kanału zrzutowego.
Obliczenie rozmyć poniżej upustu.
1 Opis techniczny
1.1 Wybór lokalizacji zapory i trasy bystrza
Lokalizacja zapory i trasy bystrza przedstawiona jest na dołączonej mapce (załącznik 1). Przy wyborze lokalizacji kierowano się dwoma kryteriami:
- kryterium topograficzne,
- kryterium utrzymania NPP
1.2 Warunki posadowienia: geologiczne, topograficzne
Zakładam, że w profilu glebowym znajdują się piaski średnie. Warunki topograficzne istniejące w pobliżu zapory są bardzo dobre do odprowadzenia wody przez upust stokowy. Nachylenie stoku jest w przybliżeniu równe 8%, grunty mineralne zapewniają odpowiednią nośność. Nie występują żadne trudności w posadowieniu budowli w istniejących warunkach.
1.3 Opis zaprojektowanej konstrukcji
Projektowana konstrukcja to upust stokowy. Upust ten przecina zaporę w jednym miejscu. Upust składa się z koryta zbiorczego o spadku 3%, bystrza o spadku 9%, niecki wypadowej płaskiej o głębokości 0,70 m i długości 3,9 m, ścianki szczelnej długości 6m zlokalizowanej za niecką wypadową w celu ograniczenia rozmyć i przesiąków. Na długości bystrza projektowane są elementy sztucznej szorstkości o wysokości 0,17 m.
1.4 Eksploatacja i obsługa upustu
Projektowany upust jest budowlą stale działającą niewymagającą obsługi. Nie posiada również zamknięć ruchomych wymagających otwarcia bądź zamknięcia na czas. Woda przelewa się stale po przekroczeniu normalnego poziomu piętrzenia 262,20 m.n.p.m. Zaleca się, aby okresowo usuwać grubsze nieczystości, które mogłyby ograniczyć przepustowość upustu.
1.5 Technologia robót wykonawczych
Ze względu na ograniczony czas budowy, podstawowe elementy konstrukcyjne budowli są prefabrykowane i łączone na miejscu budowli. Pozostałe prace wykonywane są w terenie. Na połączeniach elementów występują uszczelnienia gumowe pokryte warstwą z tworzyw sztucznych. Beton użyty do budowy jest wysokiej jakości, o wygładzonych powierzchniach o współczynniku szorstkości n = 0,015.
1.6 Przeprowadzenie wody w okresie budowy
Woda budowlana przeprowadzana będzie za pomocą spustu ulokowanego w dnie zapory. Za wylotem ze spustu odprowadzana będzie dalej przez koryto rzeki. Spust ten nie jest przedmiotem obliczeń.
Określenie rzędnej korony zapory
Zapora powinna zapewnić piętrzenie na poziomie normalnym jak również powinna uwzględniać okresowe wyższe stany wody. Rzędną zapory określiłam korzystając z rozporządzenia 111 z 1996 r. Rozporządzenie to podaje odpowiednie zapasy jakie należy uwzględnić dla danej klasy budowli. Dla klasy trzeciej budowli poziom korony zapory powinien być minimum 0,7 m do poziomu NPP i minimum 1m powyżej NPP. Określono rzędną korony 1,5 m powyżej normalnego poziomy piętrzenia, czyli na rzędnej 264,00 m.n.p.m.
3 Obliczenia hydrauliczne
3.1 Wlotu
3.1.1 Dobór wymiarów
Przyjmuję, że przelew jest niezatopiony i ![]()
m
![]()
m
![]()
=0,25 m
![]()
m
Określam szerokość obliczeniową koryta zbiorczego ze wzoru:
![]()
gdzie:
m - współczynnik wydatku uzależniony od H i r [-],
B - obliczeniowa szerokość koryta zbiorczego [m],
g - przyśpieszenie ziemskie 9,81 m/s2,
H0 - wysokość ponad normalnym poziomem piętrzenia [m],
Q=32 m3/s
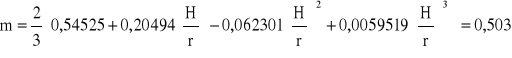
[-]
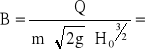
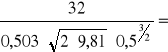
40,60 m = 41 m
Poprawnie dobrane wymiary koryta powinny spełniać następujące trzy warunki:
1) 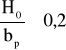
,
2) 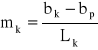
![]()
3) qk=![]()
= (3-5) ![]()
Wyznaczam ![]()
![]()
m => bp ≥ 2,5 m
Przyjmuję ![]()
= 4,5 m
Przyjmuję ![]()
= 4,0 ![]()
,
A zatem ![]()
= ![]()
= 8 m
Wyznaczam ![]()
z funkcji trygonometrycznych :
Lp =![]()
= ![]()
=18,25![]()
18,30 m
Rozpatruję warunek 2) i wyznaczam Lk:
bk - bp = 3,5 ![]()
0,2 Lk
Lk =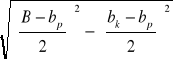
= 18,17 ![]()
18,20 m
Przyjmuję Lk = 18,20 m
Wyznaczam ![]()
- wsp. rozejścia ścian bystrza i ![]()
- wsp. nachylenia ścian
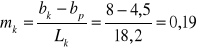
< 0,2 = > warunek spełniony
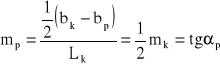
![]()
![]()
Rys. 1 Schemat koryta zbiorczego.
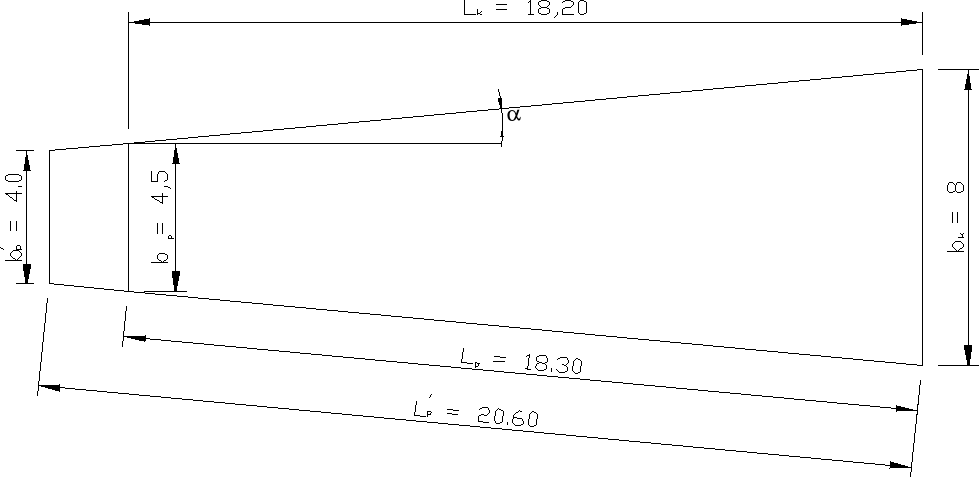
Wydłużam ![]()
![]()
m
![]()
=20,60 m
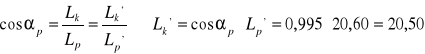
m
![]()
m
Przepływ jednostkowy na długości przelewu
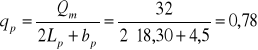
![]()
Przepływ jednostkowy na długości koryta
![]()
![]()
![]()
![]()
Wyznaczam spadek koryta ![]()
![]()
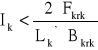
![]()
m
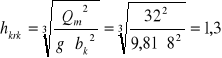
m
Fkrk = ![]()
![]()
= 8![]()
= 10,4 m2
![]()
0,13 [-]
![]()
= 0,0423 [-]
Woda w korycie zbiorczym powinna płynąć ruchem nadkrytycznym, czyli spadek koryta powinien być mniejszy od spadku końcowego krytycznego.
Przyjęto spadek dna koryta ![]()
= 0,03 = 3 %
3.1.2 Obliczenie układu zwierciadła wody
Rzeczywiste napełnienie na końcu koryta
![]()
m
Rzeczywiste napełnienie na początku przelewu
![]()
m
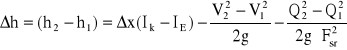
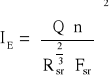
Tabela 1. Zestawienie obliczeń do określenia układu zwierciadła wody w korycie zbiorczym.
|
Tab.1 Zestawienie obliczeń układu zw. wody w korycie zbiorczym |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lp |
hi |
hzał |
x' |
bx |
Qx |
Qs |
Fx |
Fs |
Rx |
Rs |
Ie ^ 0,5 |
Ie |
Vx |
Δhobl |
1 |
2,100 |
0,002 |
20,50 |
8,00 |
36,9 |
36 |
16,80 |
16,91 |
1,377 |
1,380 |
|
0,00066 |
2,20 |
0,035 |
2 |
2,102 |
|
19,5 |
8,10 |
35,1 |
|
17,02 |
|
1,384 |
|
|
|
2,06 |
|
3 |
2,102 |
0,002 |
18,5 |
7,89 |
33,3 |
34,2 |
16,57 |
16,79 |
1,371 |
1,377 |
0,025 |
0,00061 |
2,01 |
0,018 |
4 |
2,104 |
0,002 |
17,5 |
7,68 |
31,5 |
32,4 |
16,15 |
16,36 |
1,359 |
1,365 |
0,024 |
0,00058 |
1,95 |
0,019 |
5 |
2,106 |
0,006 |
16,5 |
7,47 |
29,7 |
30,6 |
15,72 |
15,93 |
1,346 |
1,353 |
0,024 |
0,00055 |
1,89 |
0,019 |
6 |
2,112 |
0,002 |
15,5 |
7,26 |
27,9 |
28,8 |
15,32 |
15,52 |
1,335 |
1,341 |
0,023 |
0,00052 |
1,82 |
0,020 |
7 |
2,114 |
0,002 |
14,5 |
7,05 |
26,1 |
27 |
14,89 |
15,11 |
1,321 |
1,328 |
0,022 |
0,00049 |
1,75 |
0,020 |
8 |
2,116 |
0,016 |
13,5 |
6,84 |
24,3 |
25,2 |
14,46 |
14,68 |
1,307 |
1,314 |
0,021 |
0,00049 |
1,68 |
0,021 |
9 |
2,132 |
0,020 |
12,5 |
6,63 |
22,5 |
23,4 |
14,12 |
14,29 |
1,297 |
1,302 |
0,021 |
0,00042 |
1,59 |
0,023 |
10 |
2,152 |
0,023 |
11,5 |
6,42 |
20,7 |
21,6 |
13,81 |
13,96 |
1,288 |
1,293 |
0,020 |
0,00038 |
1,50 |
0,024 |
11 |
2,175 |
0,025 |
10,5 |
6,21 |
18,9 |
19,8 |
13,50 |
13,65 |
1,279 |
1,283 |
0,018 |
0,00038 |
1,40 |
0,025 |
Rys. 2 Układ zwierciadła wody w korycie zbiorczym.
3.1.3 Krzywa wydatku
Tab. nr 2. Obliczenie przepustowości koryta zbiorczego
Rzędna wody |
Hk |
Qk |
H |
H/r |
m |
k2 |
k1 |
Ls |
Kz |
Qp |
|
1 |
253,8 |
0 |
0 |
|
|
|
|
|
|
|
|
2 |
253,9 |
0,1 |
0,245 |
|
|
|
|
|
|
|
|
3 |
254 |
0,2 |
0,693 |
|
|
|
|
|
|
|
|
4 |
254,1 |
0,3 |
1,274 |
|
|
|
|
|
|
|
|
5 |
254,2 |
0,4 |
1,961 |
|
|
|
|
|
|
|
|
6 |
254,3 |
0,5 |
2,741 |
|
|
|
|
|
|
|
|
7 |
254,4 |
0,6 |
3,603 |
|
|
|
|
|
|
|
|
8 |
254,5 |
0,7 |
4,540 |
|
|
|
|
|
|
|
|
9 |
254,6 |
0,8 |
5,547 |
|
|
|
|
|
|
|
|
10 |
254,7 |
0,9 |
6,618 |
|
|
|
|
|
|
|
|
11 |
254,8 |
1 |
7,752 |
|
|
|
|
|
|
|
|
12 |
254,9 |
1,1 |
8,943 |
|
|
|
|
|
|
|
|
13 |
255 |
1,2 |
10,190 |
|
|
|
|
|
|
|
|
14 |
255,1 |
1,3 |
11,490 |
|
|
|
|
|
|
|
|
15 |
255,2 |
1,4 |
12,840 |
|
|
|
|
|
|
|
|
16 |
255,3 |
1,5 |
14,240 |
|
|
|
|
|
|
|
|
17 |
255,4 |
1,6 |
15,688 |
|
|
|
|
|
|
|
|
18 |
255,5 |
1,7 |
17,181 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
19 |
255,6 |
1,8 |
18,720 |
0,1 |
0,4 |
0,503 |
0,813 |
0,989 |
0,249 |
0,988 |
1,147 |
20 |
255,7 |
1,9 |
20,301 |
0,2 |
0,8 |
0,503 |
0,863 |
0,989 |
0,342 |
0,983 |
3,430 |
21 |
255,8 |
2 |
21,925 |
0,3 |
1,2 |
0,503 |
0,898 |
0,989 |
0,436 |
0,979 |
6,527 |
22 |
255,9 |
2,1 |
23,589 |
0,4 |
1,6 |
0,503 |
0,927 |
0,989 |
0,529 |
0,974 |
10,315 |
23 |
256 |
2,2 |
25,294 |
0,5 |
2 |
0,503 |
0,950 |
0,989 |
0,622 |
0,970 |
14,715 |
24 |
256,1 |
2,3 |
27,038 |
0,6 |
2,4 |
0,503 |
0,971 |
0,989 |
0,715 |
0,965 |
19,672 |
25 |
256,2 |
2,4 |
28,821 |
0,7 |
2,8 |
0,503 |
0,989 |
0,989 |
0,808 |
0,961 |
25,142 |
26 |
256,3 |
2,5 |
30,641 |
0,8 |
3,2 |
0,503 |
1,006 |
0,989 |
0,902 |
0,956 |
31,092 |
27 |
256,4 |
2,6 |
32,497 |
0,9 |
3,6 |
0,503 |
1,022 |
0,989 |
0,995 |
0,951 |
37,492 |
28 |
256,5 |
2,7 |
34,390 |
1,0 |
4 |
0,503 |
1,036 |
0,989 |
1,088 |
0,947 |
44,315 |
29 |
256,6 |
2,8 |
36,318 |
1,1 |
4,4 |
0,503 |
1,049 |
0,989 |
1,181 |
0,942 |
51,540 |
30 |
256,7 |
2,9 |
38,281 |
1,2 |
4,8 |
0,503 |
1,062 |
0,989 |
1,274 |
0,938 |
59,146 |
31 |
256,8 |
3 |
40,278 |
1,3 |
5,2 |
0,503 |
1,074 |
0,989 |
1,367 |
0,933 |
67,115 |
32 |
256,9 |
3,1 |
42,309 |
1,4 |
5,6 |
0,503 |
1,085 |
0,989 |
1,461 |
0,929 |
75,430 |
33 |
257 |
3,2 |
44,372 |
1,5 |
6 |
0,503 |
1,096 |
0,989 |
1,554 |
0,924 |
84,075 |
34 |
257,1 |
3,3 |
46,468 |
1,6 |
6,4 |
0,503 |
1,107 |
0,989 |
1,647 |
0,920 |
93,037 |
Rys. nr 3 Krzywe wydatku w korycie zbiorczym.
Wniosek: jak pokazują powyższe krzywe, szerokość końcowa koryta zbiorczego jest na tyle szeroka, że nie następuje dławienie. Przepływ przez koryto będzie determinowany przez przelew nad koroną.
3.2 Obliczenia bystrza
Strumień nienapowietrzony
Tab. nr 3 Układ zwierciadła wody w bystrzu.
h |
F |
u |
v |
us |
Fs |
Rs |
Ie |
Δ L |
ΣΔ L |
1,53 |
12,24 |
11,06 |
3,072 |
10,960 |
11,84 |
1,080 |
0,001 |
-0,305 |
-0,305 |
1,43 |
11,44 |
10,86 |
3,287 |
|
|
|
|
|
|
1,33 |
10,64 |
10,66 |
3,534 |
10,760 |
11,04 |
1,026 |
0,002 |
-0,139 |
-0,444 |
1,23 |
9,84 |
10,46 |
3,821 |
10,560 |
10,24 |
0,970 |
0,002 |
0,084 |
-0,359 |
1,13 |
9,04 |
10,26 |
4,159 |
10,360 |
9,44 |
0,911 |
0,003 |
0,393 |
0,034 |
1,03 |
8,24 |
10,06 |
4,563 |
10,160 |
8,64 |
0,850 |
0,004 |
0,835 |
0,869 |
0,93 |
7,44 |
9,86 |
5,054 |
9,960 |
7,84 |
0,787 |
0,005 |
1,491 |
2,360 |
0,83 |
6,64 |
9,66 |
5,663 |
9,760 |
7,04 |
0,721 |
0,007 |
2,516 |
4,875 |
0,73 |
5,84 |
9,46 |
6,438 |
9,560 |
6,24 |
0,653 |
0,010 |
4,232 |
9,108 |
0,63 |
5,04 |
9,26 |
7,460 |
9,360 |
5,44 |
0,581 |
0,015 |
7,417 |
16,525 |
0,53 |
4,24 |
9,06 |
8,868 |
9,160 |
4,64 |
0,507 |
0,025 |
14,442 |
30,966 |
0,375 |
3 |
8,75 |
12,533 |
8,905 |
3,62 |
0,407 |
0,056 |
87,722 |
118,688 |
Rys. nr 4 Układ zwierciadła w bystrzu.
Przyjęto spadek bystrza według załączonej mapki 9%, czyli i = 0,09
Obliczono h0 ze wzoru:
![]()
sinၡ = 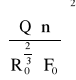
gdzie:
Q - natężenie przepływu w bystrzu [m3/s],
n - chropowatość w bystrzu ( przyjąłem dla betonu wygładzonego 0,015 ),
R0 - promień hydrauliczny w przekroju bystrza przy wysokości h0 [m],
F0 - pole przekroju koryta bystrza przy wysokości h0 [m2],
Obliczenia przeprowadzono metodą kolejnych przybliżeń zakładając wartość h0.
W wyniku podstawienia otrzymałem h0= 0,29 m
F0 = ![]()
=![]()
m2,
U0 = ![]()
m,
R0=![]()
m
sin(6,03) = 0,105
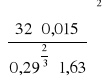
= 0,1
L ≈ P
W celu zmniejszenia prędkości w bystrzu projektuje bystrze ze sztuczną szorstkością pokazane na rys nr 5.
Rys. nr 5 Schemat sztucznej szorstkości w bystrzu.
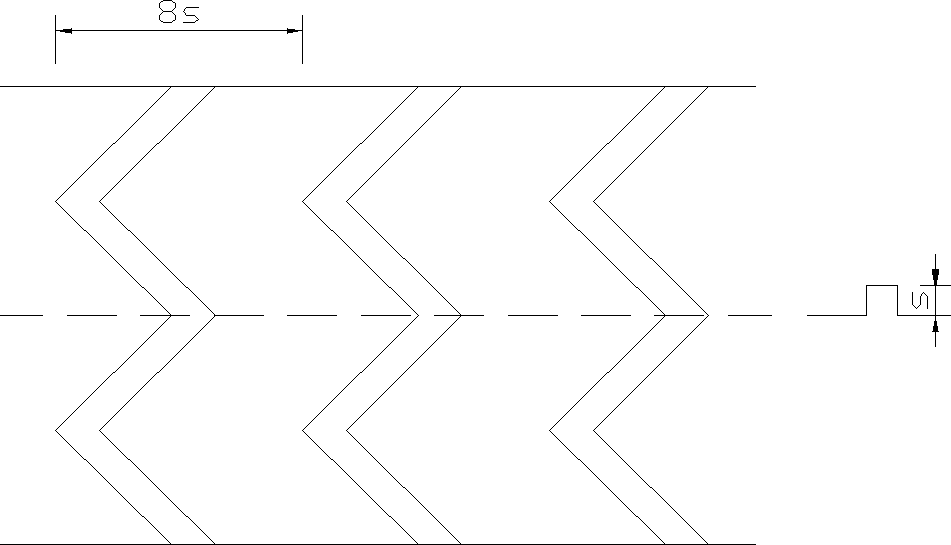
Wyznaczam wysokość, dla której prędkość w bystrzu wynosi 5 m/s, (jest to prędkość dopuszczalna dla koryta wykonanego z betonu):
Q = 32 m3/s
v = 5 m/s
b = 8 m
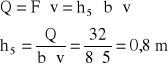
Dla h5 = 0,8 m wyznaczam c.
c - współczynnik Chezy,
F5 = 8·0,8=6,4 m2 - pole przekroju przy wysokości h5,
U5 = 8+2·0,8=9,6 m - obwód zwilżony przy wysokości h5,
R5 = 0,67 m - promień hydrauliczny,
Jb = 0,09 spadek bystrza,
Q = ![]()
32 = ![]()
→ c = 20,36
Dla tej wartości odczytano z tabeli 3.14 wartości:
![]()
, ![]()
h0C = 1,33 m , s = 1,6 m
Ponownie obliczam c dla wysokości h0C = 1,33 m
F = 10,64 m2 ,
U = 10,66 m ,
R = 0,998 m ,
Q = ![]()
32 = ![]()
→ c = 10,04
V = ![]()
3,0 m/s
Prędkość jest mniejsza od dopuszczalnej prędkości V = 5 m/s.
Zaprojektowana szorstkość w bystrzu jest dobrze dobrana.
Obliczenia sprawdzające, czy wystąpi falowanie w bystrzu.
h0 = 1,33 m ,
Fr0 = 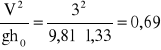
,
F = 10,64 m2 ,
U = 10,66 m2 ,
R = 0,998 m ,
ၡ = ![]()
,
c = 10,04 ,
cosၡ = 0,994 ,
![]()
m2/s ,
n = 0,015 ,
k1 = 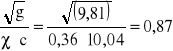
k2 = 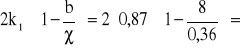
-36,93
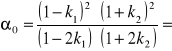
0,4
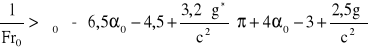
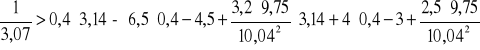
1,45 < 5,09
Wynika stąd, że wystąpi falowanie na długości bystrza.
Obliczam maksymalną wysokość fali:
hmax= 0,25![]()
1,21 m
Obliczam średnią długość fali:
lśr = 30h0 = ![]()
m
Fale które wystąpią w bystrzu będą występować co 39,9 m, a ich wysokość nie powinna przekraczać 1,21 m.
Strumień napowietrzony
Wyznaczam wartość ![]()
=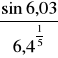
=0,072
q - jednostkowe natężenie przepływu na szerokości bystrza [m3/s.m],
Korzystając z nomogramu rys. 10.82 „ Podstawy melioracji rolnych” P. Prochal tom 2
Wykres do wyznaczania głębokości ha i prędkości Va strumienia napowietrzonego, określono ![]()
, ![]()
, stąd ha = 1,04 m, Va = 4,99 m/s
Dla tak małej wartości jak 0,072 współczynnik koncentracji powietrza jest bardzo mały i wynosi mniej niż 0,2. Jest to zgodne z tym, co wcześniej wyliczono, czyli, że nie występuje w tym przypadku strumień napowietrzony.
3.3 Obliczenia urządzeń do rozpraszania energii
Określenie położenia wysokościowego wypadu
Rys. 6 Schemat odskoku hydraulicznego.
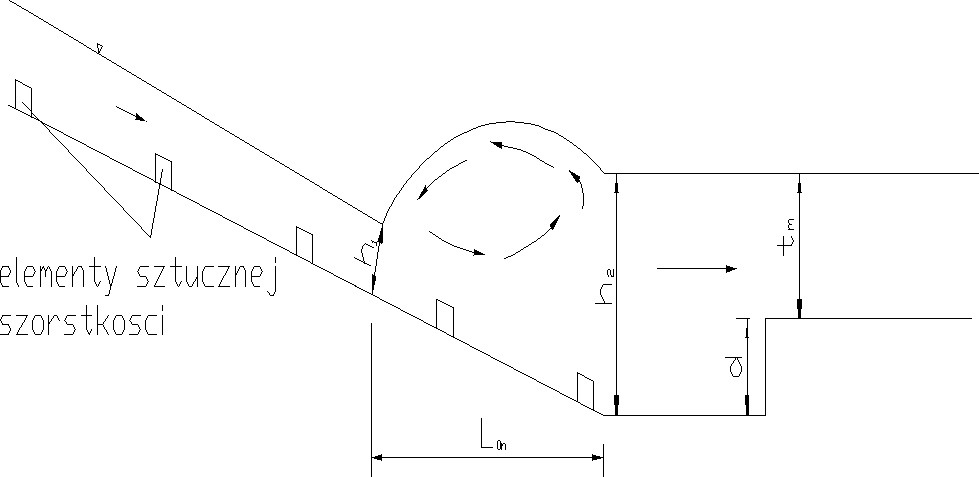
tm - napełnienie w stanowisku dolnym przy natężeniu przepływu Qm ,
tm = 1,55 m,
Lm = ![]()
m ,
h1 = h0 = 1,33 m ,
၄h = tm - h1cosၡ = 1,55-![]()
1,55-![]()
m ,
L1= ![]()
m ,
Qm = 32 m3/s ,
q = Q/b = 32/8 = 4,0 m3/s.m ,
F = 10,64 m2 ,
U = 10,66 m2 ,
R = 0,998 m ,
V = 3,0 m/s
Fr0 = 0,69 ,
h2p = 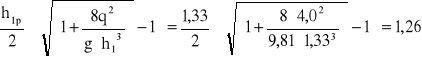
m
E1 = 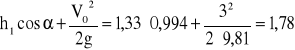
m
ctgၤ = 0,3Fr0 + 0,54 = 0,75
ၤ = 53,13Ⴐ
Druga wysokość sprzężona wynosi 1,26 m,
Obliczam drugą wysokość sprzężoną odskoku nachylonego.
h1p = h1n = 1,33 m ,
tg ၡ = 0,106 ,
Odczytano wartość K z rysunku 4.33 z książki A. Żbikowski i in. „Hydrauliczne podstawy projektów wodnomelioracyjnych” (str. 289)
K = f(tg ၡ) = 2,5 ,
Pozostałe oznaczenia jak powyżej
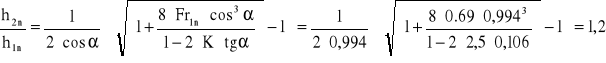
h2n = 1,2 · 1,33 = 1,6 m ,
L0n = ![]()
m
i < tg ၡ
3.3.2 Obliczenie długości wypadu
Długość niecki wypadowej przyjmuję w przybliżeniu 3h2p , co daje w sumie 3,9 m.
3.3.3Dobór kształtu i wymiarów wypadu.
Obliczenia głębokości niecki wypadowej
Obliczenia wykonuję dla trzeciego przypadku, tzn. h2n > tm, bo 1,6 m > 1,55 m ,
n = 1,05 ,
d = nh2n - tm = 1,05 · 1,6 - 1,55 = 0,67 m
Przyjmuję d = 0,7 m ,
h2n' = tm + d = 1,55 + 0,7 = 2,25 m ,
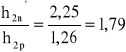
,
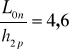
- odczytane z rys. 4.34 z książki A. Żbikowski i in. „Hydrauliczne podstawy projektów wodnomelioracyjnych” (str. 290) ,
L0n = h2p · 4,6 = 1,26 · 4,6 = 5,8 m ,
Przyjęto długość odskoku równą:
L0n = 6,0 m ,
Głębokość niecki 0,70 m przyjmuję za ostateczną. Nie projektuję poszerzenia koryta.
4 Dobór umocnień i obliczenie rozmyć poniżej upustu.
Długość i rodzaj umocnień kanału doprowadzającego.
Lu = (2 ÷ 3)b =
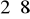
=16 mLu ≤ 20 m
Lu =
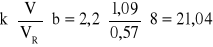
m,
V - prędkość w stanowisku dolnym,
VR - prędkość dopuszczalna dla gruntu z tematu,
b - szerokość koryta,
V = ![]()
m/s,
F = 0,5 · (8 + 14,75) · 1,70 = 18,91 m2 ,
Umocnienia kanału doprowadzającego muszą być sztywne, a zatem na długości 19 m projektuję płyty betonowe.
Rodzaj umocnień kanału zrzutowego.
Na kanale zrzutowym projektuję umocnienia skarp w postaci narzutu kamiennego. Dno kanału zrzutowego jest wykonane z gruntu naturalnego, czyli piasku grubego.
Obliczenie rozmyć poniżej upustu.
Do obliczeń przyjmuję schemat Rossińskiego
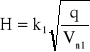
,
gdzie:
H - głębokość rozmycia ,
k1 - współczynnik uwzględniający wzmożoną burzliwość strumienia,
przyjmuję k1 = 1,7 dla umocnień na poziomie dna stanowiska dolnego i zakończone ścianą szczelną ,
q - jednostkowe natężenie przepływu w stanowisku dolnym,
Vn1 - prędkość nierozmywająca przy głębokości 1 m ,
Przyjmuję prędkość Vn1 = 0,57 m/s dla mojego gruntu (piasek średni) z tematu na podstawie tabeli 4.2 z książki A. Żbikowski i in. „Hydrauliczne podstawy projektów wodnomelioracyjnych” (str. 350) ,
q = ![]()
,
Bz = b + 0,4·2·tm = 8 + 0,4 · 2 · 1,55 = 9,24 m
q = ![]()
m3/sm ,
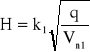
=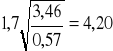
m ,
![]()
Powyższe obliczenia wskazują na fakt, iż nie nastąpi rozmycie dna gdyż nachylenie jest mniejsze od 1:3.
7
Wyszukiwarka