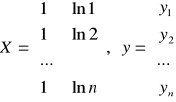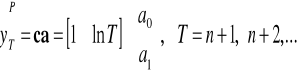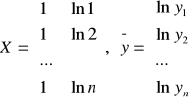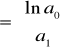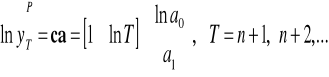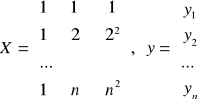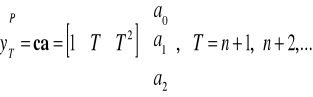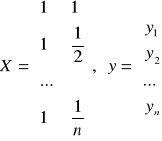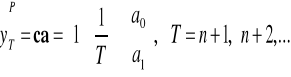TREND LINIOWY

Dany jest szereg czasowy:
. Szereg ten może być opisywany funkcją trendu i wówczas:

gdzie:
to funkcja trendu,
to składnik losowy.

Gdy funkcja trendu jest postaci:
, to mówimy, że mamy do czynienia z trendem liniowym.

Możemy to zapisać w postaci macierzowej następująco:

,

gdzie:
ma wymiary nx1, X ma wymiary nx2, a ma wymiary 2x1,
ma wymiary nx1.

Szacowanie parametrów metodą najmniejszych kwadratów:

,

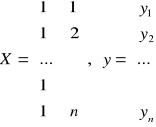
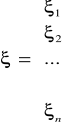
Założenia:

ma n-wymiarowy rozkład normalny
, gdzie
to macierz jednostkowa o wymiarach nxn.

,

Interpretacja parametrów strukturalnych modelu:

Współczynnik kierunkowy określa o ile jednostek zmienią się (wzrosną lub spadną) wartości zmiennej
gdy czas wzrośnie o jednostkę.

Wyraz wolny określa przeciętną wartość zmiennej
dla czasu

Weryfikacja modelu

Miary dopasowania:

• Wariancja resztowa:
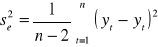
  , gdzie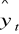
  to wartości teoretyczne modelu.

• Odchylenie standardowe składnika resztowego:
  

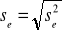
INT: odchylenie standardowe składnika resztowego określa o ile jednostek wartości rzeczywiste odchylają się przeciętnie od wartości teoretycznych.

• Współczynnik zmienności resztowej:
  

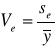
INT. Współczynnik zmienności resztowej określa jakim procentem średniej wartości zmiennej rzeczywistej jest odchylenie standardowe składnika resztowego.

• Współczynnik zbieżności:
  

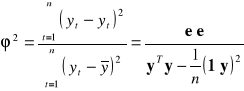
INT. Określa jaki procent zmienności zmiennej objaśnianej nie został wytłumaczony zmiennością czasu poprzez liniową funkcję trendu.

• Współczynnik determinacji liniowej:
  .

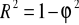
INT. Określa jaki procent zmienności zmiennej prognozowanej został wytłumaczony zmiennością czasu poprzez liniową funkcję trendu.

Prognoza punktowa

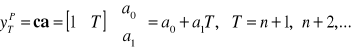
Mierniki ex ante:

Ocenę ex ante średniego błędu predykcji (odchylenia standardowe błędu prognozy):

Interpretacja: średni błąd ex ante mówi, jaka jest oczekiwana różnica pomiędzy rzeczywistą wartością zmiennej a jej prognozą.

Ocena ex ante względnego błędu predykcji: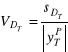

Interpretacja: względny błąd ex ante mówi, jaki procent prognozy stanowi średni błąd ex ante.

Dopuszczalność prognoz. Mówimy, że prognoza jest dopuszczalna wtedy, gdy względny błąd ex ante nie przekracza ustalonej wartości progowej (tutaj przyjmujemy, że wartość ta wynosić będzie 10%). Jeśli wartość progowa zostanie przekroczona, mówimy, że prognoza nie jest dopuszczalna.

Prognoza przedziałowa (przedstawiona postać wykorzystuje założenie normalności składników losowych)

, gdzie

Interpretacja: Z prawdopodobieństwem
rzeczywista wartość zmiennej (
) będzie znajdować się w przedziale

Precyzja predykcji

Precyzja predykcji
- połowa długości przedziału predykcji

Względna precyzja predykcji
obliczana ze wzoru postaci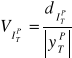

INT. Z prawdopodobieństwem
maksymalny błąd prognozy przedziałowej wynosi
, co stanowi
prognozy punktowej.

Trend wykładniczy

Wykładnicza funkcja trendu przyjmuje postać:

W celu oszacowania parametrów funkcji wykładniczej przy pomocy metody najmniejszych kwadratów należy dokonać linearyzacji modelu, co sprowadza się do zlogarytmowania równania. Otrzymuje się więc równanie:

które jest liniowe ze względu na parametry:

Szacowanie parametrów metodą najmniejszych kwadratów:

,

,

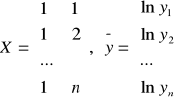
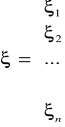
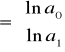
Weryfikacja modelu

Miary dopasowania:

• Wariancja resztowa:
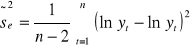
  , gdzie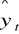
  to wartości teoretyczne modelu.

• Odchylenie standardowe składnika resztowego:
  

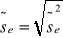
Prognoza punktowa

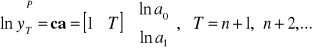
(to jest logarytm z prognozy)

(to jest właściwa prognoza zm Y)

Mierniki ex ante:

Ocena ex ante średniego błędu predykcji:

Interpretacja: średni błąd ex ante mówi, jaka jest oczekiwana różnica pomiędzy rzeczywistą wartością zmiennej a jej prognozą.

Ocena ex ante względnego błędu predykcji: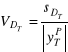

Interpretacja: względny błąd ex ante mówi, jaki procent prognozy stanowi średni błąd ex ante.

Prognoza przedziałowa

, gdzie

Interpretacja: Z prawdopodobieństwem
rzeczywista wartość zmiennej (
) będzie znajdować się w przedziale

Precyzja predykcji

Precyzja predykcji
- połowa długości przedziału predykcji

Względna precyzja predykcji
obliczana ze wzoru postaci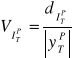

INT. Z prawdopodobieństwem
maksymalny błąd prognozy przedziałowej wynosi
, co stanowi
prognozy punktowej.

Zestawienie wzorów dla pozostałych funkcji trendu

Trend logarytmiczny

Wzór
Transformacja	brak
Postacie macierzy	,
Prognoza
Błędy ex ante

Trend potęgowy

Wzór
Transformacja
Postacie macierzy	,
Prognoza
Błędy ex ante

Trend paraboliczny

Wzór
Transformacja	brak
Postacie macierzy	,
Prognoza
Błędy ex ante

Trend hiperboliczny

Wzór
Transformacja	brak
Postacie macierzy	,
Prognoza
Błędy ex ante

Sezonowość: modele wskaźnikowe

MODEL ADDYTYWNY WZORY

Postać modelu:

- wartość szeregu czasowego w okresie (momencie)
, przy czym
czyli wartość w l - tym cyklu j-tej fazy, N - liczba cykli, m - liczba faz w cyklu.

f - funkcja trendu opisująca tendencję rozwojową,

g_j - bezwzględne wahanie sezonowe dla j-tej fazy cyklu,

składnik losowy.

Etapy specyfikacji modelu i wyznaczania prognoz:

ETAP 1 Wyodrębnienie trendu (oszacowanie parametrów odpowiedniej funkcji trendu)

ETAP 2 Eliminacja trendu:

, (różnica pomiędzy wartościami rzeczywistymi oraz trendem)

ETAP 3 Wyznaczenie surowych bezwzględnych wahań sezonowych

(średnie odchylenie pomiędzy wartościami rzeczywistymi oraz trendem dla wybranej fazy cyklu tj. np. dla wszystkich II kwartałów)

ETAP 4 Wyznaczenie oczyszczonych bezwzględnych wahań sezonowych

(od surowego wahania sezonowego odejmujemy średnią z surowych wahań sezonowych)

Oczyszczone bezwzględne wahania sezonowe spełniają warunek:

INTERPRETACJA oczyszczonych bezwzględnych wahań sezonowych:
informuje o ile jednostek wartości zmiennej Y w j-tej fazie cyklu różnią się przeciętnie od wartości wyznaczonych przy pomocy funkcji trendu.

ETAP 5. Wyznaczenie prognoz punktowych

(tzn. ekstrapolujemy funkcję trendu i dodajemy odpowiednią wartość bezwzględnego wahania sezonowego)

MODEL MULRIPLIKATYWNY WZORY

Postać modelu:

- wartość szeregu czasowego w okresie (momencie)
, przy czym
czyli wartość w l - tym cyklu j-tej fazy, N - liczba cykli, m - liczba faz w cyklu.

f - funkcja trendu opisująca tendencję rozwojową,

w_j - wskaźnik sezonowości dla j-tej fazy cyklu,

składnik losowy.

Etapy specyfikacji modelu i wyznaczania prognoz:

ETAP 1 Wyodrębnienie trendu (oszacowanie parametrów odpowiedniej funkcji trendu)

ETAP 2 Eliminacja trendu:

, (iloraz pomiędzy wartościami rzeczywistymi oraz trendem)

ETAP 3 Wyznaczenie surowych wskaźników sezonowych

ETAP 4 Wyznaczenie oczyszczonych bezwzględnych wahań sezonowych

, gdzie

Własność:
(tzn. suma oczyszczonych wskaźników sezonowych równa się liczbie faz w cyklu tj. np. dla danych kwartalnych 4, dla miesięcznych 12 itd.)

INTERPRETACJA:
informuje o ile procent wartość zmiennej Y w j-tej fazie cyklu jest większa (wtedy w_j jest większe od 1) lub mniejsza (
) przeciętnie od wartości wyznaczonych przy pomocy funkcji trendu.

ETAP 5. Wyznaczenie prognoz punktowych

(tzn. ekstrapolujemy funkcję trendu i mnożymy przez odpowiednią wartość wskaźnika sezonowego)

OCENA TRAFNOŚCI PROGNOZ

Mierniki ex post dokładności predykcji

(Obciążenie prognoz) Średni poziom błędu predykcji ex post:

m liczba jednostek czasu w okresie empirycznej weryfikacji prognoz

I_ep - okres empirycznej weryfikacji prognoz (okres - w którym porównujemy otrzymane prognozy z wartościami rzeczywistymi)

Interpretacja: wartość ta informuje i ile jednostek prognozy były przeciętnie większe (prognozy przeszacowane) lub mniejsze (prognozy niedoszacowane) od wartości rzeczywistych.

Średni względny poziom błędu predykcji ex post: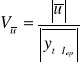

Interpretacja: mówi jaki procent średniej wartości zmiennej w okresie empirycznej weryfikacji prognoz stanowił średni poziom błędów ex post.

Średni błąd predykcji ex post :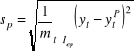

Interpretacja: informuje i ile jednostek wartości prognoz różniły się przeciętnie od wartości rzeczywistych w okresie empirycznej weryfikacji prognoz

Względny błąd predykcji ex post :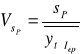

Interpretacja: mówi jaki procent średniej wartości zmiennej w okresie empirycznej weryfikacji prognoz stanowił średni błąd predykcji ex post.

LINIOWY MODEL EKONOMETRYCZNY

Postać modelu :
,

Szacowanie parametrów MNK:

gdzie: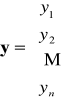
,
,
,

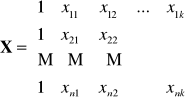
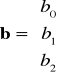
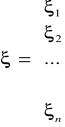
Interpretacja parametrów.

Współczynnik
wskazuje o ile jednostek zmieni się (wzrośnie lub spadnie) wartość zmiennej objaśnianej Y jeśli
wzrośnie o jednostkę, a pozostałe zmienne zostaną niezmienione.

.

Weryfikacja modelu (interpretacja taka jak w modelu liniowym)

Miary dopasowania: Wariancja resztowa:

• Odchylenie standardowe składnika resztowego:
  

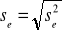
• Współczynnik zmienności resztowej:
  

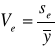
• Współczynnik zbieżności:
  .

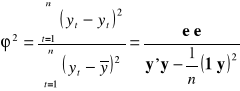
• Współczynnik determinacji liniowej:
  

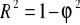
Ocena istotności parametrów strukturalnych modelu

hipoteza zerowa
wobec alternatywnej

=

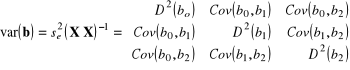
statystyka testowa:

wartość krytyczna:
,

gdzie k - liczna szacowanych parametrów,

jeśli
: na poziomie istotności
odrzucamy hipotezę zerową mówiącą, że parametr
jest nieistotny statystycznie , na korzyść hipotezy mówiącej, że jest on statystycznie istotny.

jeśli
to mówimy, że na poziomie istotności
nie ma podstaw do odrzucenia hipotezy zerowej mówiącej, że parametr
jest nieistotny statystycznie.

Prognozy zmiennej objaśnianej:

Prognoza punktowa:
lub
gdzie :

Gdzie:
to prognozy zmiennych objaśniających na okres T.

Mierniki ex ante

• Ocena ex ante średniego błędu predykcji:
  =

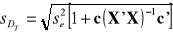
• Ocena ex ante względnego błędu predykcji:
  

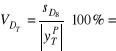
Prognoza przedziałowa:
,

Ad. 7.

Mierniki ex ante

• Precyzja predykcji
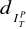
  - połowa długości przedziału predykcji ,

• Względna precyzja predykcji
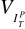
  obliczana ze wzoru postaci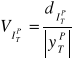
  

Przykładowe zadania

Zad 1. Roczne obroty [w mln zł] firmy handlowej „Karamba” w latach 2000-2006 zostały opisane przy pomocy następującego modelu:
. Dodatkowo wyznaczono:

,
,

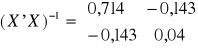
1. Zinterpretować współczynnik funkcji trendu.

2. Ocenić dobroć dopasowania funkcji do danych empirycznych.

3. Wyznaczyć prognozy punktowe.

4. Wyznaczyć błędy ex ante.

5. Wyznaczyć prognozy przedziałowe.

6. Ocenić precyzję predykcji.

Zad 2. Przychody branży kosmetycznej w województwie małopolskim w latach 1998-2006 została opisana przy pomocy następującego modelu:
. Dodatkowo wyznaczono:

,
.

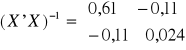
1. Wyznaczyć prognozę punktową na 2007r.

2. Wyznaczyć prognozę przedziałową na 2007r.

3. Wyznaczyć błędy ex ante na 2007r.

4. Wyznaczyć prognozę przedziałowa na 2007r.

Zad 3. Kwartalne zużycie wody [w tys. litrów] lokatorów spółdzielni mieszkaniowej „Zróbtosam” w latach 2003-2006 zostało opisane przy pomocy trendu:

oraz bezwzględnych wahań sezonowych dla pierwszych trzech kwartałów:-0,6; -0,2; 1,1.

1. Zinterpretować współczynnik kierunkowy funkcji trendu.

2. Wyznaczyć i zinterpretować brakującą wartość wahania sezonowego

3. Wyznaczyć prognozę punktową na II i IV kwartał 2007 roku.

4) Na podstawie danych z lat 1999-2005 dotyczących: wpływów dewizowych Polski z turystyki przyjazdowej - przychody ogółem w mld USD Yt, liczby przyjazdów turystów zagranicznych do Polski (w mln) X1, oraz liczby turystów zagranicznych korzystających z bazy noclegowej (w mln) X2 oszacowano model przyczynowo-opisowy:

; Dodatkowo wyznaczono:

,
,
,
.

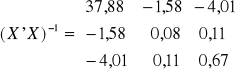
1. Zinterpretować parametry strukturalne modelu.

2. Wyznaczyć prognozę punktową zm Y na 2006 i 2007 rok.

---