CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie wartości współczynników wnikania ciepła dla konwekcji swobodnej w przestrzeni nieograniczonej i konwekcji wymuszonej. Określa się także wpływ promieniowania cieplnego na wartość współczynnika wnikania ciepła dla konwekcji swobodnej oraz porównuje wartości wyznaczonych doświadczalnie i obliczonych teoretycznie współczynników wnikania ciepła dla konwekcji wymuszonej.

1. KONWEKCJA WYMUSZONA

Lp...	u	Temperatura powietrza								Czas napełniania Zbiorniczka kondensatu [s]				Obj. kond. [m^3]
				wlot				wylot
				1	2	3	śr.	1	2	3	śr.	1	2		3	śr.
1	7,23	24,4	24,6	24,6	24,5	62,6	62,6	62,7	62,6	158	162	163	161	0,00004
2	5,84	25,6	25,2		25,4	64,4	64,4		64,4	197	191		194	0,00004
3	3,95	26,2	25,8	25,7	25,9	55,8	66,0	65,8	62,5	248	251	249	249	0,00004
4	2,84	26,0	26,3	26,1	26,1	66,1	66,0	66,0	66,0	271	289	285	281	0,00004

Tabela wyników pomiarów

Na podstawie otrzymanych wartości pomiarowych obliczamy strumień ciepła ze wzoru:




gdzie:

V_k - objętość kondensatu w zbiorniczku pomiarowym [m³]

ρ_k - gęstość kondensatu (w 40°C) = 992,2 [kg/m³]

r - ciepło kondensacji pary wodnej pod ciśnieniem atmosferycznym [J/kg]

τ - czas gromadzenia kondensatu równy wartości średniej z trzech oznaczeń [s]

Przykład obliczeń dla pierwszej serii pomiarowej




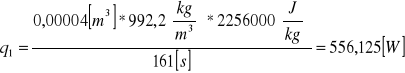
Obliczamy średnią logarytmiczną różnicę temperatur:


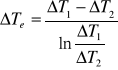
(Tutaj miał problem z tym, że nie są wpisane wyliczone Δ, wzór to 100-wartośc temperatury z tabeli)




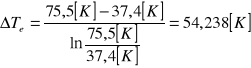
Obliczam doświadczalną wartość współczynnika wnikania ciepła ze wzoru:




gdzie:

q - strumień ciepła [W]

A - powierzchnia wymiany ciepła [m²] obliczona z wymiarów wymiennika

A = πd*h=π0,05m*1,5m=0,2356 m²





Obliczamy wartość liczby Nusselta:




gdzie:

d - średnica przewodu [m]

λ - przewodnictwo cieplne (w 40°C) = 0,02652 [W/m⋅K]




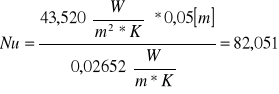
Obliczamy wartość liczby Reynoldsa:




Gdzie:

u - średnia liniowa prędkość przepływu [m/s]

d - średnica przewodu [m]

ρ - gęstość powietrza (40°C) = 1,092 [kg/m³]

η - lepkość =0,00001922 [Pa⋅s]




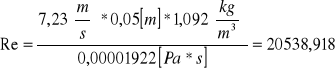
Tabela wyników obliczeń

Lp.	q1 [W]	∆T1 [K]	∆T2 [K]	∆Te [K]	α1	Re	Nu	log(Re)	log(Nu)
1	556,125	75,5	37,4	54,238	43,520	20538,918	82,051	4,313	1,914
2	461,526	74,6	35,6	52,718	37,159	16590,218	70,058	4,230	1,845
3	359,583	74,1	37,5	53,739	28,401	11221,124	53,546	4,050	1,729
4	318,634	73,9	34,0	51,394	26,315	8067,846	49,613	3,907	1,696

Wykres zależności Nu=f(Re)




Z powyższego wykresu odczytujemy współczynniki w równaniu:


(tutaj o ile dobrze pamiętam to facet stwierdził, że współczynniki ai b zostały wpisane na odwrót)

b = 10^(-0,448) = 0,356

A =0,544

II. KONWEKCJA SWOBODNA

Tabela wyników pomiarów

	Temperatura izolacji [°C]								Czas napełniania zbiorniczka kondensatu [s]				Obj. kond. [m^3]	Temp. [°C]
		górna				dolna
Lp.	1	2	3	śr.	1	2	3	śr.	1	2	3	śr.			0,00002	23
1	53,8	53,6	53,6	53,7	46,8	46,8	46,8	46,8	151	151	153	152

I sposób

Na podstawie otrzymanych wartości pomiarowych obliczamy strumień ciepła ze wzoru:







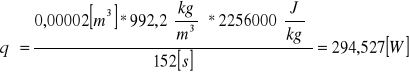
Obliczamy średnią logarytmiczną różnicę temperatur dla konwekcji swobodnej:

ΔT₁= 30,7[K]

ΔT₂=23,8 [K]







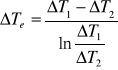
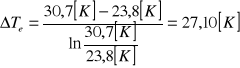
Obliczamy doświadczalną wartość współczynnika wnikania ciepła ze wzoru:




A - powierzchnia wymiany ciepła [m²] dla konwekcji swobodnej

A = 0,9891 [m²]




Obliczamy wartość współczynnika rozszerzalności objętościowej:


(to T we wzorze
plus 273 kelwiny)




Obliczamy wartość liczby Grashoffa:




g - przyspieszenie ziemskie [m/s²] = 9,81[m/s²]

ν - współczynnik lepkości kinematycznej [m²/s] = 17,6
[m²/s]

L - długość elementu grzejnego [m]




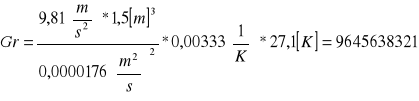
Obliczamy wartość liczby Nusselta korzystając z zależności:




Ponieważ wartość iloczynu (Gr⋅Pr) jest z zakresu 2⋅10⁷<(Gr⋅Pr)<10¹³




Obliczam teoretyczną wartość współczynnika wnikania:







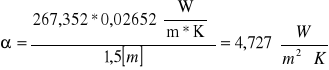
II sposób

Obliczamy wartość temperatury powierzchni osłony izolacji wymiennika:




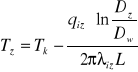
T_k - temperatura kondensacji pary [K]

D_w - średnica wewnętrzna izolacji =0,198[m]

D_z - średnica zewnętrzna izolacji =0.21[m]

λ _iz- przewodnictwo właściwe cieplne izolacji =0,036[W/(mK)]




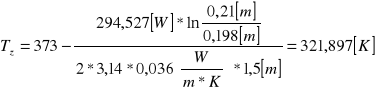
Obliczamy strumień ciepła wymieniony na drodze promieniowania:




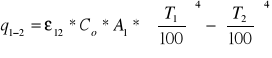
ε₁₂ - zastępczy stopień czarności obu ciał

C_o - techniczna stała promieniowania ciała doskonale czarnego = 5,76 [W/m²K⁴]

A₂>>A₁, zastępczy stopień czarności
₁₂=
₁. Przyjmujemy założenie
₁=0,04, więc
₁₂=0,04




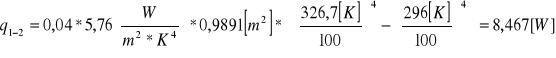
Obliczamy wartość doświadczalnego współczynnika wnikania ciepła α₃ z równania:


=>
(ΔT jest zła, powinna być wzięta taka jak w teoretycznej wartości współczynnika)

A_z - powierzchnia zewnętrzna izolacji [m²]

ΔT - różnica temperatur T_k-T_z




Tabela wyników obliczeń dla konwekcji swobodnej

q [W]	Tz [K]	Gr	Pr	q1-2 [W]	q-q1-2 [W]	α3 [W/(m^2*K)]
294,527	321,897	9645638321	0,722	8,467	286,06	5,659

Wnioski:

• W wyniku przeprowadzonego doświadczenia dla konwekcji swobodnej otrzymałyśmy wartość współczynnika wnikania ciepła α (obliczonego sposobem 2) zbliżoną do obliczonej wartości teoretycznej, co pozwala sądzić, iż nieścisłości w wartościach otrzymanych wyników są, być może, powiązane ze zbyt małą dokładnością w przeprowadzaniu pomiarów oraz, w pewnym stopniu, z zaokrąglaniem obliczanych wartości.

Natomiast dla sposobu 1 otrzymana wartość doświadczalna znacznie odbiega od obliczonej wartości teoretycznej, co może być spowodowane nieszczelną izolacją wymiennika ciepła. Wpływ na otrzymany wynik może mieć także niedokładność w przeprowadzaniu pomiarów.

• Porównując wartości α dla konwekcji swobodnej i wymuszonej otrzymaliśmy wyniki większe dla konwekcji wymuszonej, co jest logiczne i zgodne z treściami prezentowanymi w instrukcji.

•Analizując wyniki otrzymane przy obliczaniu wartości współczynnika wnikania ciepła dla konwekcji swobodnej sposobem 2 możemy stwierdzić, że im większy jest strumień ciepła wymieniony na drodze promieniowania pomiędzy ciałami, tym mniejsza jest wartość współczynnika α, co bezpośrednio wynika ze wzoru


Z błędów w sprawku był jeszcze jeden, gdzieś wzięłam zamiast średniej z dwóch temperatur jedną konkretną ale niestety nie pamiętam gdzie to dokładnie było. I w świetle tych błędów bodajże pierwszy wniosek nam się nie zgadzał. Reszta powinna być okej. Mam nadzieję, że komentarze okażą się choć trochę pomocne