POLITECHNIKA WROCŁAWSKA

WYDZIAŁ BUDOWNICTWA LĄD. I WOD.

ZAKŁAD DYNAMIKI BUDOWLI

ĆWICZENIE PROJEKTOWE

Z

DYNAMIKI BUDOWLI

ROK AKAD. 1998/99 TOMASZ RZODKIEWICZ

GR 4 ROK III

ZADANIE : Dla schematu ramy złożonej z pryzmatycznych prętów prostych rozwiązać zagadnienie

własne oraz sporządzić obwiednię dynamicznych momentów zginających. Pominąć wpływ tłumienia oraz odkształcalności osiowej prętów i odkształcalności osiowej prętów i odkształcalności postaciowej.

Zastosować metodę przemieszczeń w wersji komputerowej.

EI=const.

2m p =1,1ω₁

4m

Biegunowy moment bezwładności obrotowej masy tarczy względem środka masy :

Wielkości porównawcze : l , m , EJ , F₀

Współrzędne uogólnione :

n_h = e - 3t = 5 - 3 = 2

n_g = n_r + n_t = 6+ 2 = 8

n_d = 3

n_gd = n_g - n_d = 8-3 = 5

( 5 współrzędnych nadliczbowych )

Współrzędne lokalne :

Wyznaczenie macierzy transformacji A_m :

Stan q₁ = 1

u₁ = 1

u₂ = 0

u₃ = 0

u₄ = 0

u₅ = 0

Stan q₂ = 1

u₁ = 0

u₂ =

u₃ = 1

u₄ = 0

u₅ = 0

Stan q₃ = 1

u₁ = 0

u₂ = 0

u₃ = 0

u₄ = 1

u₅ = 0

Macierz transformacji :

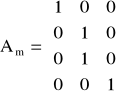
Diagonalna macierz mas:

{m} = diag ( 2,2,
,4 )

Wyznaczenie macierzy bezwładności :

1. Sposób - B = A_m^T*{m}*A_m

{m}*A_m =

A_m^T =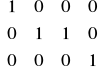

A_m^T*{m}*A_m=

B =

2. Sposób E_k =
   

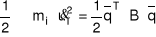
E_k =

B =
=

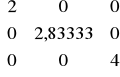
Wyznaczenie macierzy sztywności :

Schemat wyjściowy i podział na elementy :

l₁ = 5

l₂ = 3,5

l₃ = 2,5

l₄ = 4

l₅ =
3,60555

Stan q₁ = 1

Ψ₃₄ =

Ψ_5,6 = -

M₃₄ = M₄₃ =

M₅₆ = M₆₅ =

Stan q₂ = 1

ϕ₄ = 1

ϕ₅ = 1

M₄₃ =
M₃₄ =

M₅₆ =
M₆₅ =

Stan q₃ = 1

Ψ₁₂ =

Ψ₃₄ =

M₁₂ = M₂₁ =

M₅₆ = M₆₅ =

Stan X₁ = 1

ϕ₈ = 1

M₈₇ =

M₇₈ =

Stan X₂ = 1

ϕ₆ = 1

ϕ₇ = 1

ϕ₉ = 1

M₇₈ =

M₈₇ =

M₆₅ =

M₅₆ =

M_10,9 =

M_9,10 =

Stan X₃ = 1

ϕ₁₀ = 1

M_9,10 =

M_10,9 =

Stan X₄ = 1

ϕ₃ = 1

ϕ₂ = 1

M₁₂ =

M₂₁ =

M₃₄ =

M₂₁ =

Stan X₅ = 1

ϕ₁ = 1

M₁₂ =

M₂₁ =

Macierze transformacji przemieszczeń uogólnionych na przemieszczenia lokalne elementu.

;
; α_L,P = ϕ - Ψ

q₁ q₂ q₃ X₁ X₂ X₃ X₄ X₅

1 0 0 -0,33333 0 0 0 0 1

A₁ =

2 0 0 -0,33333 0 0 0 1 0

3 -0,28571 0 -0,28571 0 0 0 1 0

A₂ =

4 -0,28571 1 -0,28571 0 0 0 0 0

5 0,4 1 0 0 0 0 0 0

A₃ =

6 0,4 0 0 0 1 0 0 0

7 0 0 0 0 1 0 0 0

A₄ =

8 0 0 0 1 0 0 0 0

9 0 0 0 0 1 0 0 0

A₁ =

10 0 0 0 0 0 1 0 0

Wyznaczenie macierzy sztywności.

Wyniki obliczeń uzyskane z programu :

macierz transformacji Axq= - Kxx_1 Kxq

Axq[1,1] = 1.5084612473E-01 Axq[1,2] = 1.2570510394E-01 Axq[1,3] = 0.0000000000E+00 Axq[2,1] = -3.0169224946E-01 Axq[2,2] = -2.5141020789E-01

Axq[2,3] = 0.0000000000E+00

Axq[3,1] = 1.5084612473E-01

Axq[3,2] = 1.2570510394E-01

Axq[3,3] = 0.0000000000E+00

Axq[4,1] = 2.8102622951E-01

Axq[4,2] = -3.2786885246E-01

Axq[4,3] = 3.9577918033E-01

Axq[5,1] = -1.4051311475E-01

Axq[5,2] = 1.6393442623E-01

Axq[5,3] = 3.0210540984E-01

macierz sztywnosci K = Kqq - Kqx Kxx_1 Kxq :

K[1,1] = 6.2060699052E-01 K[1,2] = 3.8944404586E-01 K[1,3] = 8.6026866152E-02 K[2,1] = 3.8944404586E-01 K[2,2] = 2.3543753466E+00

K[2,3] = -2.6362903981E-01

K[3,1] = 8.6026866153E-02

K[3,2] = -2.6362903981E-01

K[3,3] = 7.3537154984E-02

Rozwiązanie zagadnienia własnego z wykorzystaniem macierzy sztywności K.

Bq + Kq = 0 q = ωq

( K - ω²B )*q = 0 ω² = λ

( K - λ*B )*q = 0

Warunek niezerowego rozwiązania ( q ≠ 0 ):

det ( K - λB ) = 0

Wyniki obliczeń :

lambda[1]= 3.3061700209E-03 lambda[2]= 2.7305477874E-01 lambda[3]= 8.8328381747E-01

omega [1]= 5.7499304526E-02 omega [2]= 5.2254643692E-01 omega [3]= 9.3983180276E-01

Wektory własne :

macierz własna W :

w[1,1]=-2.3630874433E-01 w[2,1]= 1.5166604639E-01 w[3,1]= 1.0000000000E+00 w[1,2]= 1.0000000000E+00 w[2,2]=-2.2267595432E-01 w[3,2]= 1.4207644766E-01 w[1,3]= 3.3474507352E-01 w[2,3]= 1.0000000000E+00

w[3,3]=-6.7878395806E-02

macierz własna w bazie poszerzonej :

wq[1,1]=-2.3630874433E-01 wq[2,1]= 1.5166604639E-01 wq[3,1]= 1.0000000000E+00 wx[1,1]=-1.6581062196E-02 wx[2,1]= 3.3162124392E-02 wx[3,1]=-1.6581062196E-02 wx[4,1]= 2.7964365232E-01

wx[5,1]= 3.6017317384E-01

wq[1,2]= 1.0000000000E+00

wq[2,2]=-2.2267595432E-01

wq[3,2]= 1.4207644766E-01

wx[1,2]= 1.2285462075E-01

wx[2,2]=-2.4570924150E-01

wx[3,2]= 1.2285462075E-01

wx[4,2]= 4.1026563912E-01

wx[5,2]=-1.3409530611E-01

wq[1,3]= 3.3474507352E-01

wq[2,3]= 1.0000000000E+00

wq[3,3]=-6.7878395806E-02

wx[1,3]= 1.7620010106E-01

wx[2,3]=-3.5240020211E-01

wx[3,3]= 1.7620010106E-01

wx[4,3]=-2.6066156245E-01

wx[5,3]= 9.6391922716E-02

Kontrola ortogonalności wektorów własnych.

macierz W^T*K*W = {k_o}

k0[1,1]= 1.3809401289E-02 k0[2,1]= 2.8421709430E-14 k0[3,1]= 5.0661697060E-12 k0[1,2]= 5.1159076975E-13 k0[2,2]= 6.0651810727E-01 k0[3,2]=-3.4425795548E-12 k0[1,3]= 4.8672177400E-12

k0[2,3]=-3.1654678878E-12

k0[3,3]= 2.7168648134E+00

macierz W^TBW = {b_o}

b0[1,1]= 4.1768575726E+00 b0[2,1]=-3.6379788071E-12 b0[3,1]= 1.3642420527E-12 b0[1,2]=-3.6379788071E-12 b0[2,2]= 2.2212323478E+00 b0[3,2]=-1.9895196601E-12 b0[1,3]= 1.3642420527E-12

b0[2,3]=-1.9895196601E-12

b0[3,3]= 3.0758684350E+00

-2.3630874433E-01 1.0000000000E+00 3.3474507352E-01 q₁

1.5166604639E-01 -2.2267595432E-01 1.0000000000E+00 q₂

1.0000000000E+00 1.4207644766E-01 -6.7878395806E-02 q₃

W= -1.6581062196E-02 1.2285462075E-01 1.7620010106E-01 X₁

3.3162124392E-02 -2.4570924150E-01 -3.5240020211E-01 X₂

-1.6581062196E-02 1.2285462075E-01 1.7620010106E-01 X₃

2.7964365232E-01 4.1026563912E-01 -2.6066156245E-01 X₄

3.6017317384E-01 -1.3409530611E-01 9.6391922716E-02 X₅

Formy własne :

1 forma

2 forma

3 forma

Wektor sił wzbudzających ( obciążeń zewnętrznych ) F(t) = F_ssin(pt) + F_ccos(pt)

p = 1,1ω₁ = 1,1*0,05749930= 0,063249

1. sposób ( z wykorzystaniem macierzy A_m )

Praca jaką wykonuje F₀ na przemieszczeniach lokalnych:

L = -1*cos(pt)*u₁ + 1*sin(pt)*u₂

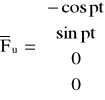
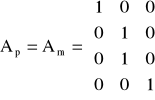
F(t) = F_ssin(pt) + F_ccos(pt)

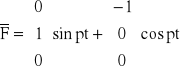
2. sposób ( metoda bezpośrednia )

Równanie pracy w miejscu zaczepienia tarczy :

L = -sin(pt)*q₁ + cos(pt)*l*q₂

stąd :

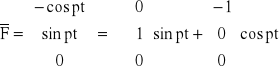
Drgania wymuszone harmoniczne. ( z wykorzyst. macierzy K )

Równanie ruchu :

Bq + Cq + Kq = F q = -p²q

gdy pomijamy tłumienie , otrzymamy :

( K - p²B )q_s = F_s

( K - p²B )q_c = F_c

stąd :

q_s =( K - p²B )^-1*F_s

q_c =( K - p²B )^-1*F_c

Rozwiązanie :

czesc sinusowa qs[1]= 1.7542094658E+01 qs[2]=-1.2110437590E+01

qs[3]=-8.1719316550E+01

xs[1]= 1.1238131828E+00

xs[2]=-2.2476263656E+00

xs[3]= 1.1238131828E+00

xs[4]=-2.3442380126E+01

xs[5]=-2.9138059615E+01

czesc kosinusowa

qc[1]= 1.2110437590E+01

qc[2]=-7.4796231362E+00

qc[3]=-5.2379374855E+01

xc[1]= 8.8658577545E-01

xc[2]=-1.7731715509E+00

xc[3]= 8.8658577545E-01

xc[4]=-1.4874979978E+01

xc[5]=-1.8751935542E+01

Wartości momentów przywęzłowych Ms, Mc

Ms[1]= 2.9103830457E-11 Mc[1]= 2.9103830457E-11

Ms[2]= 2.2782717956E+00 Mc[2]= 1.5507822254E+00

Ms[3]=-2.2782717956E+00 Mc[3]=-1.5507822254E+00

Ms[4]= 4.1971239395E+00 Mc[4]= 2.6751359700E+00

Ms[5]=-4.3343903646E+00 Mc[5]=-1.7599141723E+00

Ms[6]= 3.5558586148E+00 Mc[6]= 2.8052470959E+00

Ms[7]=-1.6857197742E+00 Mc[7]=-1.3298786632E+00

Ms[8]= 0.0000000000E+00 Mc[8]=-1.8189894035E-12

Ms[9]=-1.8701388406E+00 Mc[9]=-1.4753684327E+00

Ms[10]= 0.0000000000E+00 Mc[10]=-1.8189894035E-12

Wykresy momentów.

M_s

M_c

Amplituda momentów

amM =

pkt	am M
1	0,00000
2	2,75598
3	2,75598
4	4,97717
5	4,67806
6	4,52919
7	2,14714
8	0,00000
9	2,38205
10	0,00000

Sprawdzenie równowagi momentów gnących w przekroju zamocowania tarczy masowej.

F_s = F_o*sin(pt)

F_c = F_o*cos(pt)

Siły bezwładności :

B₁ = -2m*u₁ = 2mp²u₁

B₂ = 2m*u₂ = 2mp²u₂

B₃ = -J₀*u₃ =
ml²*p²*u₃ = 0,83333ml²*p²*u₃

u₁ = q₁

u₂ = q₂

u₃ = q₂

stąd :

B₁ = 2mp²q₁

B₂ = 2mp²q₂

B₃ = 0,8333ml²*p²*q₂

Częstość wymuszenia :

p = 0,063249

q_s =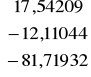
q_c =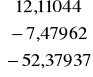

M_4s = 4,19712 M_4c = 2,67514

M_5s = -4,33439 M_5c = -1,75991

Skoki w wykresach :

ΔM_s = B₂*l + B₃ = 2mp²q_2s *l + 0,83333*ml²p²q_2s =

= 2*(0,063249)²*(-12,11044) + 0,83333*(0,063249)²*(-12,11044) =

= -0,13727

ΔM_c = B₂*l + B₃ + F_s*l= 2mp²(q_2c)*l + 0,83333*ml²p²q_2c +1*l =

= 2*(0,063249)²*(-7,47962) + 0,83333*(0,063249)²*(-52,37937)+1 =

= 0,91522

Kontrola :

M_s

ΣM = - 4,19712 + 4,33439 - 0,13727 = 0,00000

M_c

ΣM = -2,67514 + 1,75991 +0,91522 = - 0,00001

14