Zadanie 1.

Uporządkuj rosnąco, ze względu na rząd wielkości następujące funkcje:

• 
  ,
  ,
  ,
  

• 
  ,
  ,
  ,
  ,
  

• 
  ,
  ,
  ,
  ,
  

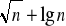
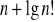
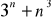
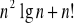
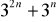
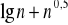
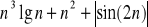
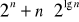
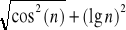
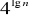
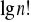
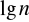
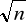
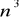
Odpowiedzi do zadania 1.

1. 
   <
   <
   <
   

2. 
   <
   <
   <
   <
   

3. 
   ,
   ,
   ,
   ,
   

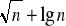
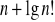
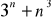
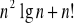
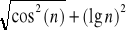
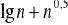
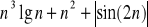
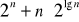
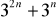
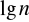
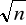
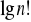
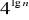
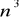
Zadanie 2.

Podaj możliwie najlepsze oszacowanie następującej funkcji stosując notację O:

Funkcja

Odpowiedzi do zadania 2.

Oszacowanie

Zadanie 3.

Podaj możliwie proste oszacowanie następującej funkcji stosując notację Θ:

Funkcja

Odpowiedzi do zadania 3.

Oszacowanie

Notacja Θ

Zapisujemy jako: f(n) = Θ(g(n))

Taki zapis oznacza, że f jest tego samego rzędu co g, czyli istnieją takie stałe c₁ i c₂ że:

c₁ · |g(n)| ≤ |f(n)| ≤ c₂ · |g(n)|

Czyli funkcja g(n) jest ograniczeniem górnym dla f (n).

• Jak sprawdzić, czy f(n) = Θ(g(n)) ?

Upewniamy się, że
lub konkretniej

Przykładowy wykres:

Zadanie 4.

Algorytm A mający złożoność obliczeniową

wykonuje się na pewnym

komputerze K dla n=100 w czasie 5 sekund.

Jak duże zadanie będziemy w

stanie rozwiązać w ciągu 5 sekund na komputerze K1

dokładnie 1024 razy szybszym niż K?

Zadanie 5.

Ile czasu zajmie wykonanie zadania dla danych wejściowych

rozmiaru 10 algorytmem A

o złożoności
wiedząc, że wykonanie zadania o

rozmiarze 12 zajmuje (przy użyciu tego samego algorytmu)

864 sekundy?

Odpowiedź do zadania 5.

Złożoność algorytmu A dla danych rozmiaru n określona jest

przez funkcję
.

Zatem dla danych rozmiaru 12 algorytm ten wykona

operacji dominujących.

Czas, jaki jest potrzebny do wykonania zadania o rozmiarze12,

wynosi dokładnie 864 sekundy, czyli wykonanie jednej operacji

dominującej

zajmuje
.

Dla danych rozmiaru 10 algorytm A wykona dokładnie

operacji dominujących, co ostatecznie zajmie
sekund.

Zadanie 6.

Na komputerze K wykonanie algorytmu A dla danych o rozmiarze 6

zajmuje 8 sekund. Złożoność tego algorytmu opisuje funkcja

.

Ile czasu będzie potrzebował komputer K1,

dokładnie 1024 razy szybszy od komputera K,

do wykonania algorytmu A dla danych rozmiaru 20?

Odpowiedź do zadania 6.

sekund

Zadanie 7.

Mamy do posortowania tablicę zawierającą milion (10⁶) liczb.

Do dyspozycji mamy

Komputer K1 - wykonujący 1 milion (10⁶) operacji na sekundę,

Komputer K2 - wykonujący 100 milionów (10⁸) operacji na sekundę.

Na komputerze K1 sortujemy przy użyciu algorytmu sortowania

przez scalanie

Na komputerze K2 sortujemy przy użyciu algorytmu sortowania

przez wstawianie

Który, komputer wykona zadanie sortowania w krótszym czasie?

Odpowiedź do zadania 7.

Komputer osobisty : wykonuje 1 milion (10⁶) operacji na sekundę

Sortujemy algorytmem przez scalanie :

Superkomputer : wykonuje 100 milionów (10⁸) operacji na sekundę.

Sortujemy algorytmem przez wstawianie:

T(10⁶) = 2 * (10⁶)2 / 108= 20 000 sekund ≈5.56 godzin

Komputer osobisty wykona zadanie 20 razy szybciej.

UWAGA: Sortowanie przez wstawianie jest szybsze od

sortowania przez scalanie dla małych n

Zadanie 8.

Dla podanego poniżej fragmentu kodu algorytmu określ jego

złożoność asymptotyczną przy użyciu notacji

for (i=sum=0;i<n;i++)

sum += a[i];

Pętla for wykonuje się n razy a podczas każdej iteracji 2 przypisania, jedno sum drugie i (2n) oraz 2 przypisania w deklaracji

2+2n = O(n)

Zadanie 9.

Dla podanego poniżej fragmentu kodu algorytmu określ jego złożoność asymptotyczną przy użyciu notacji
:

for (i = 0; i < n; i++){

for(j = 1, sum = a[0]; j<=i; j++)

sum += a[j];

cout<<"suma podtablicy od 0 do "<< i <<" to <<sum<<endl;

Zadanie 10.

Dla K=3, L=6 Podaj ile wynosi X.

Określ jego złożoność asymptotyczną przy użyciu notacji

1. Zaimplementuj algorytm przy pomocy Dev C++ 4.9.9.2

2. Określ (wraz z dowodem matematycznym) złożoność algorytmu przy użyciu notacji O.

ODPOWIEDZI DO ZADAŃ

Zadanie 4.

Złożoność algorytmu A dla danych rozmiaru n określona jest przez zależność
. Dla danych rozmiaru 100 algorytm ten wykona
operacji dominujących. Czas jaki jest potrzebny do wykonania zadania o rozmiarze 100 na komputerze K wynosi dokładnie 5 sekund. To samo zadanie (czyli
operacje dominujące) komputer K1 wykona w
sekundy. Zatem w ciągu dokładnie 5 sekund komputer K1 wykona
operacje dominujące, co ostatecznie odpowiada rozmiarowi danych wejściowych równemu
.

Zadanie 8.

Pętla for wykonuje się n razy a podczas każdej iteracji 2 przypisania, jedno sum drugie i (2n) oraz 2 przypisania w deklaracji

2+2n = O(n)

Zadanie 9.

Inicjalizacja zmiennej i,

Pętla zewnętrzna wykonywana jest n razy,. Za każdym razem wykonywana jest iteracja pętli wewnętrznej, instrukcja drukowania oraz przypisania zmiennych i, j, sum. Pętla wewnętrzna wykonywana jest i razy dla każdego
przy czym w każdej iteracji wykonywane są dwa przypisania: jedno zmiennej sum , drugie zmiennej j.

Liczba przypisań w całym programie wynosi więc: