SZEREGI LICZBOWE

1. Podstawowe określenia

(1.1) Definicja

Niech (a_n) będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg (S_n), gdzie
Szereg taki oznaczamy przez
. Liczbę a_n nazywamy n-tym wyrazem, a liczbę S_n n-tą sumą częściową tego szeregu.

(1.2) Definicja

Mówimy, że
jest zbieżny, jeżeli istnieje granica właściwa ciągu (S_n). Jeżeli
lub
to mówimy, że szereg
jest rozbieżny odpowiednio do
lub
. W pozostałych przypadkach mówimy, szereg jest rozbieżny.

Sumą szeregu zbieżnego nazywamy granicę
i oznaczamy ją tym samym symbolem co szereg.

(1.3) Twierdzenie

Jeżeli szeregi
i
są zbieżne, to

1)
;

2)
, gdzie c- stała.

(1.4) Fakt (o zbieżności szeregu geometrycznego)

Szereg geometryczny
jest zbieżny dla
i rozbieżny dla
. Dla zbieżnego szeregu geometrycznego mamy

(1.5) Twierdzenie (warunek konieczny zbieżności szeregu)

Jeżeli szereg
jest zbieżny, to

Uwaga. Twierdzenie odwrotne nie jest prawdziwe. Świadczy o tym przykład ciągu
. Mamy bowiem
, a szereg
jest rozbieżny.

2. Kryteria zbieżności szeregów

(2.1) Twierdzenie (o szeregu Dirichleta)

Szereg
jest zbieżny dla
i rozbieżny dla
.

W szczególności dla
otrzymujemy rozbieżny szereg harmoniczny
.

(2.2) Twierdzenie (kryterium porównawcze zbieżności szeregów)

Niech
dla każdego
. Wówczas:

1. jeżeli
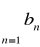
   jest zbieżny, to także szereg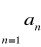
   jest zbieżny;

2. jeżeli
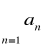
   jest rozbieżny, to także szereg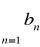
   jest rozbieżny.

(2.3) Twierdzenie (kryterium ilorazowe zbieżności szeregów)

Niech
(
) dla każdego
oraz niech

Wówczas szeregi
i
są jednocześnie zbieżne albo rozbieżne.

(2.4) Twierdzenie (kryterium d'Alemberta zbieżnośći szeregów)

Niech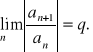
Wtedy szereg
jest zbieżny dla
i rozbieżny dla
lub

(2.5) Twierdzenie (kryterium Cauchy'ego zbieżności szeregów)

Niech
Wtedy szereg
jest zbieżny dla
i rozbieżny dla
lub

3. Zbieżność bezwzględna szeregów liczbowych

(3.1) Twierdzenie (Leibniza o zbieżności szeregu naprzemiennego)

Jeżeli ciąg (b_n) jest nierosnący od numeru
oraz

to szereg naprzemienny
jest zbieżny.

Ponadto prawdziwe jest oszacowanie:

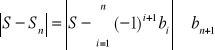
, dla każdego
,

gdzie S oznacza sumę szeregu

Uwaga. Monotoniczność ciągu (b_n) jest istotnym założeniem powyższego twierdzenia, gdyż np. ciąg
spełnia warunek
ale szereg naprzemienny
jest rozbieżny.

(3.2) Definicja (zbieżność bezwzględna szeregu)

Szereg
jest zbieżny bezwzględnie, gdy szereg
jest zbieżny.

(3.3) Twierdzenie

Jeżeli szereg jest zbieżny bezwzględnie, to jest zbieżny.

Uwaga: Twierdzenie odwrotne nie jest prawdziwe. Szereg
jest zbieżny, ale nie jest zbieżny bezwzględnie.

(3.4) Definicja (zbieżności warunkowej szeregu)

Szereg zbieżny, który nie jest zbieżny bezwzględnie nazywamy szeregiem zbieżnym warunkowo.

4. Sumy ważniejszych szeregów liczbowych:

,
,

,
,

,
.

1

4

---