2.5. Teoria niepewności

Teoria niepewności traktuje o opisie niedokładności wyniku pomiaru (albo innej operacji niedokładnej), przyjmując losowy model kreacji tego wyniku i traktując wynik pomiaru (albo innej operacji niedokładnej) jako estymatę wartości prawdziwej (albo dokładnej) daną estymatorem nieobciążonym. Dalsze rozważania będziemy odnosili do wyniku pomiaru, ale bez trudu można je uogólnić na wyniki innych operacji np. odtwarzania lub obliczania.

Niech będzie estymatą wartości prawdziwej (lub dokładnej) zmiennej x. Zmienna x może być wielkością mierzoną, może być jedną z wielkości; na podstawie których wyznacza się wartość wielkości mierzonej. Estymata może pochodzić z pomiaru, może być uzyskana w inny sposób, ale zawsze jest niedokładna. Teoria niepewności przyjmuje losowy model niedokładności zakładając, że faktycznie wyznaczona estymata jest jedną z wartości zmiennej losowej , o wartościach danych przez hipotetyczne doświadczenie powtarzanie pomiaru takie, że wartość oczekiwana zmiennej losowej jest równa wartości prawdziwej

E()   (2.48)

Inaczej, rozkład randomizowanej estymaty powinien być centrowany względem wartości prawdziwej . Powtarzanie pomiaru czy operacji wyznaczania estymaty jest jednak czysto hipotetyczne, zawsze można więc przyjąć warunki powtarzania takie, aby zachodziło (2.48). Estymata jest w stosunku do wartości prawdziwej (dokładnej) obarczona błędem . Randomizowana estymata i błąd spełniają

=  +  E() = 0

(2.49)

W [GUIDE'93] niepewność (w znaczeniu ogólnym) definiuje się jako

"parametr, związany z wynikiem pomiaru, charakteryzujący rozrzut wartości, które można w uzasadniony sposób przypisać wielkości mierzonej"

a niepewność standardową jako

"niepewność wyniku pomiaru wyrażoną jako odchylenie standardowe"

Wydaje się, że bardziej zrozumiała (a także ogólniejsza i ściślejsza) jest definicja niepewności wychodząca z dobrze ugruntowanego pojęcia błędu.

Kwadrat niepewności standardowej u2() estymaty obciążonej randomizowanym i centrowanym błędem  jest wariancją σ 2() błędu  czyli wariancją σ 2() estymaty lub estymatą wariancji (tj. wariancją eksperymentalną) s2() błędu  czyli estymatą wariancji s2() estymaty , jeżeli wariancja jest nieznana.

Zapiszemy to wzorem

u2() =



σ 2() = σ 2()  jeżeli znana jest wariancja  s2() = s2()   jeżeli znana jest tylko estymata wariancji

(2.50)

Niepewność standardowa określona wzorem (2.50) jest niepewnością standardową bezwzględną. Oprócz niej definiuje się niepewność standardową względną

(2.51)

Niepewność standardową bezwzględną u() wyraża się w jednostkach wielkości mierzonej x, niepewność standardowa względna urel() jest ułamkiem, często wyraża się ją w procentach.

Teoria niepewności preferuje określanie niedokładności za pomocą niepewności standardowej, oprócz niepewności standardowej wprowadza jednak pojęcie niepewności rozszerzonej definiując ją [GUIDE'93] jako

"wielkość określającą wokół wyniku pomiaru przedział, od którego można oczekiwać, że obejmie dużą część rozkładu wartości, które można w uzasadniony sposób przypisać wielkości mierzonej"

Definicja ta jest opatrzona uwagą

"ułamek, określający część obejmowanego rozkładu, może być traktowany jako prawdopodobieństwo objęcia lub poziom ufności przedziału."

Współczynnik rozszerzenia jest w [GUIDE'93] zdefiniowany jako

"liczbowy czynnik, przez który należy pomnożyć niepewność standardową, aby otrzymać niepewność rozszerzoną"

Uogólnimy pojęcie niepewności rozszerzonej (niepewność rozszerzona może bowiem być oceną dowolnej estymaty obciążonej błędem randomizowanym i centrowanym) utożsamiając ją z błędem granicznym liczonym metodą RiCBS. Przyjmiemy definicję

Niepewność rozszerzona U() na poziomie ufności p jest połową szerokości przedziału ufności na poziomie (ufności) p estymaty wartości prawdziwej .

Niepewność rozszerzona spełnia warunek

Pr { ∈ [  U();   U()]} ≥ p (2.52)

Niepewność rozszerzoną oblicza się jako krotność niepewności standardowej u()

U() = kp u() (2.53)

gdzie kp jest współczynnikiem rozszerzenia odpowiadającym poziomowi ufności p.

Niepewność rozszerzona określona wzorami (2.52) i (2.53) jest niepewnością rozszerzoną bezwzględną. Oprócz niej definiuje się niepewność rozszerzoną względną

(2.54)

Wartość współczynnika rozszerzenia zależy od przyjętego poziomu ufności p i od postaci rozkładu randomizowanego błędu całkowitego  estymaty . Gdyby randomizowana estymata miała rozkład normalny, a jej niepewność standardowa u() była dana jako odchylenie standardowe σ(), (czyli pierwiastek z wariancji), to współczynnik rozszerzenia kp byłby równy wartości krytycznej Zp standaryzowanego rozkładu normalnego i niepewność rozszerzoną na poziomie ufności p liczylibyśmy jako

U() = Zp u() (2.55)

Niektóre wartości krytyczne Zp są podane w Tabl. 2.4. Hipoteza o normalnym rozkładzie estymaty jest jednak generalnie niesłuszna. Zwykle przyjmuje się arbitralnie standardowe wartości współczynnika rozszerzenia i odpowiadające mu poziomy ufności, najczęściej kp  2 i p ≈ 0,95; rzadziej kp  3 i p ≈ 0,99.

Wrócimy do omawianego pomiaru składającego się z serii obserwacji (2.16). Estymatą wartości prawdziwej jest średnia arytmetyczna serii liczona ze wzoru (2.18). Estymatę randomizujemy metodą RiCBS sprowadzając ją do postaci (2.41). Estymatę wariancji randomizowanej estymaty określa wzór (2.45). Korzystając z definicji niepewności standardowej [wzór (2.50)] obliczamy niepewność standardową estymaty

u2()  u2()  u2()

(2.56)

gdzie

u2() = s2() = s2(y)/N =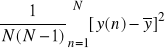
(2.57)

jest składową niepewności wywołaną rozrzutem obserwacji (tj. błędami przypadkowymi), a

u2() = σ 2() (2.58)

jest składową niepewności wywołaną błędami systematycznymi. W teorii niepewności unika się zwykle terminu błąd i niepewność u2() nazywa się raczej niepewnością poprawki, przyjmując, że błąd systematyczny można skorygować wprowadzając odpowiednią poprawkę, a "resztkowy" błąd systematyczny jest powodowany niedokładnością poprawki. Można więc nieznany błąd systematyczny  traktować jako nieznaną poprawkę. Przyjmuje się też, że niepewność u2() jest powodowana wpływem czynników przypadkowych, a niepewność u2() jest powodowana wpływem czynników systematycznych.

Czynniki systematycznie oddziaływujące na pomiar mogą mieć wiele przyczyn, ale najważniejszą z nich jest niedokładność przyrządów pomiarowych. Dla wielu przyrządów pomiarowych, zwłaszcza dla mierników elektrycznych, przy powtarzaniu pomiaru tej samej wartości wielkości mierzonej w warunkach powtarzalności, niedokładność pomiaru jest niezmienna (w języku teorii błędu powiedzielibyśmy, że ma charakter błędu systematycznego) i daje się opisać poprawką , wartość tej poprawki jest nieznana, wiadomo jednak o niej, z danych przyrządu, że mieści się w określonych granicach, w przedziale niepewności poprawki

(2.59)

gdzie D jest błędem granicznym przyrządu lub jego niedokładnością (patrz następny wykład). Błąd graniczny D jest zawsze podawany w specyfikacji przyrządu pomiarowego. Przyrządów spełniających warunek (2.59) może być wiele, każdy z nich ma swoją własną, nieznaną poprawkę  (tj. błąd systematyczny prawdziwy) różniącą się wartością od także nieznanych poprawek innych przyrządów. Poprawki przyrządów mają pewien rozkład w przedziale
.

Wyobraźmy sobie, że wykonujemy serię pomiarów przyrządem spełniającym warunek (2.59). Randomizacja estymaty i poprawki  polegałaby na hipotetycznym wykonywaniu serii obserwacji, przy czym każda seria byłaby wykonywana innym przyrządem o innej poprawce , losowość estymaty i poprawki  zapewniałoby losowanie przyrządu z populacji wszystkich przyrządów spełniających (2.59). Dla tak randomizowanej poprawki  przyjmuje się zwykle jeden z trzech rozkładów: prostokątny (R), trójkątny symetryczny (T) lub normalny (N). Rozkłady te opiera się na przedziale [D, D], umieszczając w tym przedziale rozkład poprawki cały (prostokątny i trójkątny) lub prawie cały (normalny z przedziałem [3σ, 3σ] równym przedziałowi [D, D]). Wariancje wymienionych trzech rozkładów wynoszą

(2.60)

Najczęściej przyjmuje się, że poprawka  ma rozkład prostokątny.

Uwzględniając powyższe mamy wzór określający niepewność standardową pomiaru prostego, w którym powtarzanymi obserwacjami y(n) są wskazania miernika.

u2()  s2()  D 2/3

(2.61)

Znając niepewność standardową u2() estymaty , można określić jej niepewność rozszerzoną U() na poziomie ufności p, zgodnie z równaniem (2.56) będzie ona wynosiła

U() = kp u() = kp
(2.62)

Jeżeli jeszcze przyjmiemy prostokątny rozkład poprawek , to mamy niepewność rozszerzoną pomiaru prostego

U() = kp u() = kp
(2.63)

Do ustalenia wartości współczynnika rozszerzenia kp odpowiadającego danemu poziomowi ufności p niezbędna jest znajomość rozkładu estymaty , wyznaczenie zaś tego rozkładu jest niezwykle żmudne i nie daje się rozwiązać w sposób ogólny. Zwykle więc przyjmuje się standardowe wartości współczynnika rozszerzenia: k  2 i odpowiadający mu poziom ufności p ≈ 0,95, rzadziej k  3 i odpowiadający mu poziom ufności p ≈ 0,99. Niepewność rozszerzoną pomiaru prostego liczymy więc zwykle z zależności

U() = 2 u() = 2
(2.63)

Takie postępowanie jest dopuszczalne dla N ≥ 5 i
; N ≥ 7 i
oraz dla N ≥ 10 i dowolnego stosunku
.

Wyznaczanie niepewności średniej arytmetycznej i wyznaczanie niepewności poprawki różnią się swoją ideą. [GUIDE'93] rozróżnia dwie metody obliczania niepewności:

1. metodę typu A obliczania niepewności polegającą na obliczaniu niepewności na podstawie analizy statystycznej serii obserwacji czyli serii wyników pojedynczych pomiarów powtarzanych w warunkach powtarzalności,

2. metodę typu B obliczania niepewności polegającą na obliczaniu niepewności metodami innymi niż analiza statystyczna serii obserwacji, zwykle na podstawie danych apriorycznych.

Odpowiednio do metody obliczania rozróżnia się dwa rodzaje niepewności:

1. niepewność standardową uA() obliczoną metodą typu A,

2. niepewność standardową uB() obliczoną metodą typu B.

Niepewności te składają się na niepewność estymaty , przy czym, warto to pamiętać, że sumują się kwadraty niepewności, a nie ich pierwsze potęgi

(2.64)

W naszym przypadku niepewności obliczone metodą typu A i metodą typu B wynoszą

(2.65)

Omówimy na koniec zasady zapisywania kompletnego wyniku pomiaru z użyciem niepewności jako miary niedokładności pomiaru.

Jeżeli miarą niedokładności pomiaru jest niepewność standardowa bezwzględna, to zapis kompletnego wyniku pomiaru ma postać wartości liczbowej estymaty i podanej w nawiasach wartości liczbowej niepewności standardowej u(). Niepewność w nawiasach może być przedstawiona w pełnym zapisie, przy czym ostatnia cyfra estymaty i ostatnia cyfra niepewności powinny zgadzać się co do pozycji. Można także pominąć w zapisie niepewności początkowe zera i przecinek, ostatnia podana cyfra niepewności musi zgadzać się co do pozycji z ostatnią cyfrą estymaty. Przypuśćmy, że mierzymy napięcie, niech estymata wartości napięcia wynosi 357,63 V a niepewność standardowa bezwzględna wynosi 0,07 V. Kompletny wynik pomiaru zapisać można jako

E  357,63(0,07) V lub E  357,63(7) V

Jeżeli miarą niedokładności pomiaru jest niepewność standardowa względna, to zapis kompletnego wyniku pomiaru ma postać wartości liczbowej estymaty i podanej w nawiasach niepewności standardowej urel(), koniecznie w procentach lub ppm-ach. Przypuśćmy, że mierzymy napięcie, niech estymata wartości napięcia wynosi 357,63 V a niepewność standardowa względna wynosi 0,02 %. Kompletny wynik pomiaru zapisać można jako

E  357,63(0,02 %) V lub E  357,63(200 ppm) V

Jeżeli miarą niedokładności pomiaru jest niepewność rozszerzona bezwzględna lub względna, to zapis kompletnego wyniku pomiaru ma postać

 =  ± U() (2.79)

 =  [1 ± Urel()] (2.80)

przy czym zalecane jest podawanie wartości współczynnika rozszerzenia kp przyjętego do obliczenia niepewności rozszerzonej. Jeżeli przyjmuje się współczynnik rozszerzenia inny niż 2 lub 3, to należy podać sposób jego wyznaczania i odpowiadający mu poziom ufności. Jeżeli dla przykładowej wartości estymaty napięcia i niepewności standardowej przyjmiemy współczynnik rozszerzenia k  2 (co daje poziom ufności nie mniejszy niż 0,95), to kompletny wynik pomiaru zapiszemy w postaci

E  (357,63 ± 0,14) V (ze współczynnikiem rozszerzenia k  2)

E  357,63(1 ± 0,04 %) V (ze współczynnikiem rozszerzenia k  2)

Wartości liczbowe estymaty oraz niepewności u(), urel(), U() i Urel() są liczbami przybliżonymi, w procesie ich obliczania, zwłaszcza kiedy do obliczeń używa się kalkulatora lub komputera, otrzymuje się ich obliczone wartości wyrażone wieloma cyframi i zachodzi potrzeba zaokrąglania zarówno esytmaty jak i niepewności. Estymatę zaokrągla się według reguł zaokrąglania normalnego, niepewności zaokrągla się tak jak błędy graniczne.

Janusz M. Jaworski

METROLOGIA ELEKTRYCZNA

Wykład 2

Str. 18

---