Tatiana Zaszkowska 6 XII 2001

Ćwiczenie nr 43

Temat: Wyznaczanie współczynników temperaturowych rozszerzalności liniowej i oporu elektrycznego dla metali i stopów.

Teoria

Rozszerzalność liniowa w zależności od temperatury przedstawia się następująco:

. Jest to zależność liniowa. Współczynnik
nosi nazwę współczynnika temperaturowego rozszerzalności liniowej.

W ćwiczeniu wykorzystywane jest zjawisko termoelektryczne Seebecka, które polega na wystąpieniu siły elektromotorycznej w obwodzie złożonym z dwóch kawałków różnych metali, których połączone końce znajdują się w różnych temperaturach. Sam taki obwód złożony z połączonych ze sobą na końcach kawałków dwóch różnych metali nazywamy termoparą. Wielkość siły termoelektrycznej występującej w termoparze opisuje prawo Avenariusa
, gdzie
oznacza różnicę temperatur pomiędzy końcami termopary,
jest stałą charakterystyczną dla danej pary metali, zaś
jest temperaturą punktu neutralnego - jest to temperatura gorętszego spojenia termopary, przy której występuje największa siła termoelektryczna dla zadanej temperatury chłodniejszego spojenia.

Siłę termoelektryczną występującą w termoparze można mierzyć włączając w obwód woltomierz. Ma w tym przypadku zastosowanie prawo trzeciego metalu tzn. wprowadzenie do obwodu metali A i B trzeciego metalu C nie wpływa na wartość wypadkowej siły termoelektrycznej, pod warunkiem, że oba końce przewodu z metalu C znajdują się w takiej samej temperaturze.

Jeżeli do końców przewodnika doprowadzimy napięcie U, to wytworzone w ten sposób pole elektryczne spowoduje przepływ prądy o natężeniu I. Prawo Ohma mówi, że stosunek napięcia między dwoma punktami przewodnika do natężenia przepływającego przezeń prądy jest wielkością stałą i nie zależy ani od napięcia ani od natężenia prądu. Stosunek ten nazywamy oporem:
. Zależność oporu od temperatury jest następująca:
, gdzie
jest temperaturowym współczynnikiem oporu.

Obliczenia

, gdzie
jest kątem nachylenia wykresu
do osi

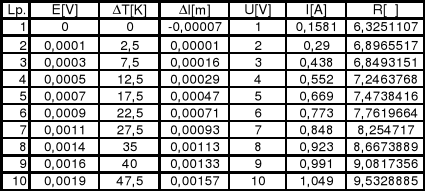
, gdzie
jest kątem nachylenia wykresu
do osi

dla 7

dla 8

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla
i
:

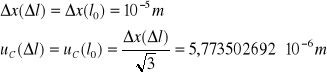
Niepewność całkowita dla
:

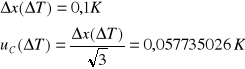
Niepewność całkowita dla U i U₀:

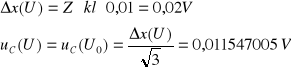
Niepewność całkowita dla I i I₀:

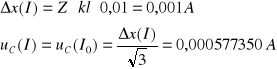
Wartości pochodnych cząstkowych:

Podstawiając wszystkie wartości otrzymujemy:

Niepewność rozszerzona (dla
k=2) wynosi:

Po zaokrągleniu niepewności rozszerzonej do dwu cyfr znaczących otrzymujemy wyniki pomiaru:

Wnioski

Zależność rozszerzalności liniowej ciał od temperatury wiąże się z budową cząsteczkową ciał stałych, w naszym przypadku - metali. Cząsteczki powiązane są ze sobą siłami sprężystości i oddziaływania międzycząsteczkowego. Wraz ze wzrostem temperatury rośnie ruchliwość cząsteczek i maleją ich drogi swobodne. Maleje również natężenie, tym samym rośnie opór.

4

---