KRYSTALOGRAFIA - to geometria kryształu, która służy do opisu struktury kryształu i jego symetrii. Strukturą kryształu nazywamy podanie położenia elementów tworzących kryształ (atomy, jony, cząsteczki) tak aby układ ten spełniał którąś z symetrii kryształu.

Struktura Kryształu

1)kształt komórki elem(jej parametry)

2)Grupa symetrii przestrzennej-klasy sym

3)Położenia atomów w kom elementarnej

1.

Kryształ to substancja, w której węzły sieci są uporządkowane w czasie i w przestrzeni, jest to uporządkowanie dalekiego zasięgu. Stan amorficzny (szkło) występuje tu uporządkowanie w czasie, natomiast uporządkowanie w przestrzeni nie, czyli jest to uporządkowanie krótkiego zasięgu, (jest to tak jakby zdjęcie migawkowe stanu ciekłego). Kryształ musi wykazać anizotropię, czyli jego właściwość zależy od kierunku, w którym go badamy.

2.

Monokryształ - kawałek jednego kryształu

Polikryształ - „zbity” z małych monokryształów, posiada swoje naturalne ściany

Krystalit - nie ma swoich naturalnych ścian

3.

Prosta sieciowa - w krystalografii, w modelu kryształu zwanym jego siecią przestrzenną, każda prosta przechodząca przez co najmniej dwa węzły sieci,

Prosta sieciowa - Jeśli dany punkt A0 poddamy translacji a otrzymując punkt A1, ten znowu poddamy translacji a dla otrzymania punktu A2 i powtarzamy tę czynność zarówno dla translacji +a, jak i -a otrzymamy dalsze punkty A3, A4...An oraz A-1, A-2 ... A-n tworzymy nieograniczony zbiór punktów identycznych. Punkty te leżą na jednej prostej, którą nazywamy prostą sieciową.

Jeśli naszą prostą sieciową A0, A1 ,A2 , A3 ...An poddamy translacji b nierównoległej do tej prostej i powtórzymy tę operację zarówno w dodatnim, jak i ujemnym kierunku to otrzymany płaszczyznę sieciową.

Płaszczyzna sieciowa, w krystalografii, w modelu kryształu zwanym jego siecią przestrzenną, każda płaszczyzna przechodząca przez co najmniej trzy węzły sieci nie leżące na jednej prostej

Dwa wektory nierównoległe wyznaczają płaszczyznę sieciowa.

Jeśli naszą płaszczyznę sieciową Auv poddamy translacji c nierównoległej do tej płaszczyzny i powtórzymy tę czynność nieograniczona liczbę razy to otrzymamy sieć przestrzenną. Np.: dwie proste sieciowe wyznaczają płaszczyznę sieciową.

Sieć krystaliczna - układ atomów wzdłuż pewnych prostych, po pewnych płaszczyznach, można spodziewać się defektów (np.: atom w innym miejscu)

Sieć przestrzenna - twór matematyczny, zbiór punktów, który odzwierciedla sieć krystaliczną, nie ma defektów.

4. , 8.

Komórka elementarna - najmniejsza liczba jonów, atomów, cząsteczek, która przez powielenie daje sieć przestrzenną całego kryształu. Komórka elementarna jest zawsze równoległościanem zbudowanym na trzech bokach a,b,c i trzech kątach ,  , γ . Jednocześnie bok jest długością wektora. Istnieją wektory jednostkowe , które nie mogą być równoległe u, v ,w .te trzy wektory ustalają porządek w trzech kierunkach w krysztale.

Komórka prymitywna jest to komórka, która ma węzły siei w narożach, zawiera minimalną ilość atomów, jest ona jedną z komórek elementarnych

5. , 6.

Równanie prostej sieciowej

x : y : z = ua :vb : wc

x/a : y/b : z/c = u : v : w

Trzy liczby całkowite [uvw] jednoznacznie określają kierunek prostej sieciowej w wybranym układzie współrzędnych; nazywamy je wskaźnikami Millera danej prostej. Na prostej [uwv] najkrótsza translacja w kierunku tej prostej przeprowadza punkt (000) w punkt P(ua, vb ,wc). np.: punkt na osi X ma wskaźniki [100] , na Y - [010], na Z - [001].

Równanie płaszczyzny sieciowej

Ogólnie xcos + ycos + zcosγ = n

Gdy płaszczyzna przechodzi przez początek układu współrzędnych xcos + ycos + zcosγ = 0

x = u1a ; y = v1b ; z = w1c

(u1a)cos + (v1b)cos + (w1c)cosγ = 0

(u2a)cos + (v2b)cos + (w2c)cosγ = 0

acos : bcos : ccosγ = h : k : l

h = v1w2 - v2w1

k = w1u2 - w2u1

l = u1v2 - u2v1

gdy płaszczyzna przechodzi przez początek układu współrzędnych

Rodzina płaszczyzn równoległych jest całkowicie

scharakteryzowana przez trzy liczby (hkl), które nazywamy wskaźnikami (wg Millera) i dla odróżnienia od wskaźników prostej [uvw] ujmujemy w nawias okrągły (hkl).

Np.: wszystkie płaszczyzny o wskaźnikach (0kl) są równoległe do osi X, (h0l) - do Y, (hk0) - do Z.

Wskaźniki Millera informują nas na ile części należy podzielić odpowiednie jednostki osiowe, aby znaleźć punkty przecięcia z osiami układu.

9.

Układy krystalograficzne

abc, γ ukł. trójskośny

abc, , γ=90 ukł. jednoskośny

abc, γ=90 ukł. rombowy (ortorombowy)

abc, γ=90 ukł. tetragonalny

abc, γ=90 ukł. regularny

abc, , γ=120 ukł. heksagonalny (trygonalny)

10.

Mamy 14 typów sieci Bravais'go, w nich jest 7 komórek prymitywnych (w których węzły sieci znajdują się w narożach). Węzły można jeszcze dodać i tak centrować przestrzennie, w środku, na ścianach. W sieci, która ma komórkę centrowaną można wybrać komórkę prymitywną. Tylko komórka prymitywna jest komórką najmniejszą (zawiera najmniej atomów) komórką w krysztale, natomiast komórka centrowana nie jest najmniejsza. Typy komórek Bravais'go dla poszczególnych sieci:

sieć trójskośna P

sieć jednoskośna P,C

sieć rombowa (ortorombowa) P,I,C,F

sieć tetragonalna P,I

sieć regularna P,I,F

sieć heksagonalna (trygonalny) P

sieć romboedryczna P

P - Np=8*1/8=1 węzły 0,0,0

C - Nc=8*1/8+2*1/2=2 węzły 0,0,0 ; ½, ½, 0

F - Nf=8*1/8+6*1/2=4 węzły 0,0,0 ; ½, 0, ½; 0,½, ½; ½, ½, 0;

J - Nc=8*1/8+1=2 węzły 0,0,0 ; ½, ½, ½

13. Przekształcenia izometryczne

Przekształcenie nazywamy izometrycznym, jeśli odległości dowolnych dwóch punktów zbioru {U} po przekształceniu w {U'} nie ulegają zmianie. Do przekształceń izometrycznych należą:

- translacja

- przekształcenie względem środka symetrii (inwersja)

- odbicie w płaszczyźnie zwierciadlanej

- obrót wokół osi symetrii n-krotnej

Przekształcenie izometryczne nie zmienia nam punktów położenia tzn. sześcian po przekształceniu izometrycznym jest nadal sześcianem. Operacje, które nie zmieniają nam obiektu (np.: obrót sześcianu o 90) nazywamy niezmienniczymi , czyli nie zmieniają one położenia w przestrzeni.

14.Operacje symetrii możliwe w sieci krystalicznej

Obrót o oś, inwersja (centrum inwersji),odbicie przez płaszczyznę

15. Iloczyn i grupa przekształceń

Jeżeli przekształcenie T1 wykonane w zbiorze {U} dało zbiór {V}, a przekształcenie T2 przeprowadza zbiór {V} w zbiór {W} i jeżeli istnieje takie przekształcenie T3, które zbiór {U} przeprowadza bezpośrednio w zbiór {W}, to przekształcenie T3 nazywamy iloczynem T2 i T1.

{V}=T1{U} ; {W}=T2{V}=T2T1{U} ; {W}=T3{U}

Euler udowodnił, że iloczynem dwóch osi jest zawsze oś.

Grupa to zbiór elementów spełniających warunki:

- element można nazwać identycznością E

- do grupy należą elem. spełniające relację Cn*Cn^-1=E

- do grupy należą dowolne iloczyny Cn^I *Cn^II *Cn^III

- kolejność mnożenia daje elem. należące do tej grupy A*B=C ; B*AC

- składniki A*B i B*A należą do grupy

16.Klasy symetrii, a układy krystalograficzne

Klasy symetrii dzielimy na rodziny ze względu na podgrupy)tylko osie 2- i4 krotne II)układ ukośnokatny 3- i 6 krotne III) połączenie I i II

Klasy krystalograficzne, klasy symetrii kryształów, zbiory kryształów podobnych pod względem symetrii ich wewnętrznej budowy, stanowiące klasy równoważności (w sensie teorii zbiorów). Kryształy dwóch różnych substancji (lub odmian polimorficznych jednej substancji) należą do tej samej klasy krystalograficznej, jeśli posiadają te same makroskopowe elementy symetrii punktowej wynikające z ich wewnętrznej budowy (mogą się natomiast różnić tzw. mikroskopowymi (przestrzennymi) elementami symetrii, czyli należeć do różnych typów grup przestrzennych i, tym bardziej, różnych typów struktur).

Każdy kryształ można zaliczyć do jednej (i tylko jednej) z 32 klas krystalograficznych kryształów. Klasy krystalograficzne, którym odpowiada z kolei zbliżona symetria punktowa, są następnie łączone w większe zespoły klasyfikacyjne kryształów, zwane układami krystalograficznymi. Z powyższego wynika, że klasy krystalograficzne zawierają się w układach krystalograficznych.

17. Symbolika klas symetrii punktowej

Symbolika Kreutza-Zaremby

Opracowana przez S.Kreutz i S.Zaremba w 1919 r.

Symbole zastosowane w tej symbolice oparte są na

koncepcji elementów twórczych grupy. Jako symbol grupy został użyty najmniejszy zbiór elementów, z których przez tworzenie potęg i ich iloczynów można wyprowadzić całą grupę. W tej symbolice zwykła nie-inwersyjna obrotu oznacza się ogólnie jako L^n, gdzie n oznacza krotność osi. Dodatkowo L^n zawiera subskrypt określający oś układu współrzędnych, z którą dana oś się pokrywa. C -oznacza centrum inwersji, P - płaszczyznę symetrii (subskrypt oznacza oś układu współrzędnych, do której płaszczyzna ta jest prostopadła. Symbol Az^4 oznacza zwierciadlaną oś symetrii pokrywającą się z osią z. Wadą tej symboliki jest rozwlekłość symboli oraz operowanie wskaźnikami górnymi i dolnymi, co utrudnia pisanie tych symboli na maszynie.

Symbolika Schónfliesa

Opracowana w 1891 r. Symbolika wprowadza następujące oznaczenia:

C - jedna oś symetrii; D - oś symetrii i osie dwukrotne do niej prostopadłe. Za pionową oś uważa się tę o najwyższej krotności. Subskrypty v, h i d oznaczają obecność płaszczyzn symetrii: v-pionowej, h - poziomej, d - diagonalnej, przebiegającej wzdłuż przekątnej. T - oznacza zespół osi symetrii charakteryzujący czworościan umiarowy. O - zespół osi symetrii charakteryzujący ośmiościan umiarowy. Np.: Cnv -jedna oś pionowa o krotności n i n płaszczyzn pionowych przecinających się wzdłuż tej osi.

Symbolika międzynarodowa Hermanna-Mauguina

W symbolice międzynarodowej, obecnie najszerzej stosowanej obowiązują następujące oznaczenia:

n - oś symetrii o krotności n; n - oś inwersyjna o krotności n; m -płaszczyzna symetrii, nm - n-krotna oś symetrii i n płaszczyzn przecinających się wzdłuż tej osi; n/m - n-krotna os symetrii i prostopadła do niej płaszczyzna symetrii; n2- n-krotna oś symetrii i n osi dwukrotnych do niej prostopadłych, n/mm - n-krotna oś symetrii i płaszczyzny symetrii do niej prostopadłe i równoległe. W tej symbolice należy pamiętać, że znaczenie cyfry i litery oznaczającej element symetrii w symbolu grupy zależy od miejsca, w którym element ten występuje.

18. Przekształcenia otwarte: translacje, osie śrubowe i płaszczyzny poślizgowe

Przekształcenia otwarte - przekształcenie, które nigdy nie prowadzi do otrzymania punktu wyjściowego, lecz każdorazowo wyznacza nowy punkt.

Translacja - jeżeli wszystkie punkty należące do utworu geometrycznego U przesuniemy równolegle o odcinek a, to operację przekształcenia U w U' nazwiemy translacją.

Oś śrubowa - jest iloczynem przekształcenia względem L^=N i równoległej translacji wynoszącej p/n, gdzie  jest periodem sieci w kierunku równoległym do osi L^n, p zaś liczbą całkowitą 0,1,2,3 ..(n-1), określającą składową translacyjną osi śrubowej.

Płaszczyzny poślizgowe - stanowią one iloczyn odbicia w płaszczyźnie i translacji. Wyróżniamy płaszczyzny poślizgowe:

-osiowe a,b,c ; a0/2,b0/2,c0/2. Przyjmują położenia (100), (010), (001)

-diagonalne : n (a0+b0)/2, (c0+b0)/2 , (a0+c0)/2; regularny, tetragonalny (a0+b0+c0)/2 - połowa długości głównej przekątnej

-diamentowe : d (a0+b0)/4, (c0+b0)/4 , (a0+c0)/4; regularny, tetragonalny (a0+b0+c0)/4

19. Grupy symetrii przestrzennej

W celu wyprowadzenia wszystkich grup przestrzennych należy do elementów twórczych poszczególnych klas dołączyć wszystkie dopuszczalne w danej klasie translacje (tzn. grupę Bravais'go oraz składowe śrubowe i składowe płaszczyzn zwierciadlano-translacyjnych) i dla tych zbiorów wyznaczyć wywiedzione z nich przekształcenia. Pełną dyskusję przeprowadzili po raz pierwszy Fedorow (1853 - 1919) i Schóenflies (1853 - 1929) niemal równocześnie w 1891 r. , lecz zupełnie niezależnie od siebie i zupełnie różnymi metodami. Obaj doszli do wniosku, że istnieje 230 grup przestrzennych.

20. Symbole grup symetrii przestrzennej

Międzynarodowe symbole grup przestrzennych opracowane przez Hermanna i Mauguina, składają się z symboli grupy translacyjnej Bravais'go oraz symboli operatorów grupy punktowej rozwiniętych przez zaznaczenie składowych translacyjnych. Porządek symboli opiera się na tej samej konwencji pozycyjnej, która obowiązuje w grupach punktowych. Rozwinięcie symboli polega na uzupełnieniu symboli osi przez podanie wskaźników płaszczyzny symetrii m odpowiednimi symbolami płaszczyzn translacyjno-zwierciedlanych: a,b,c,n,d jeżeli w danej grupie występują.

21. Pozycje wyckoffa - miejsca w sieci o określonej symetrii, która jest określona podgrupą danej grupy.. Pozycja Wyckoffa mówi nam o symetrii i krotności położenia elementukryształu.

22.Właściwości promieniowania rentgenowskiego

Promieniowanie rentgenowskie to wycinek widma fal elektromagnetycznych, której długości mieszczą

się w zakresie 0,2 A<  <2,5 A. Długość tego

promieniowania idealnie „trafia” w rozmiary atomów i odległości miedzypłaszczyznowe. Promieniowanie dotyczy przejścia miedzy wew. elektronami. Lampa rentgenowska emituje promieniowanie złożone, które dzięki filtracji można wyciąć określone częstotliwości.

Są niewidzialne dla oka, lecz naświetlają kliszę fotograficzną, Rozchodzą się prostoliniowo, interferują wzajemnie i ulegają ugięciu, co świadczy o ich falowym charakterze, Przenikają przez wiele materiałów nieprzezroczystych dla światła, zwłaszcza przez materiały o niewielkim ciężarze właściwym, jak drewno, aluminium, tkanka miękka; Są pochłaniane przez inne materiały o dużym ciężarze właściwym, np. ołów, częściowo zaś przez inne metale, kości itp.

Pojęcia

Kąt odbłysku 0 kat pomiędzy płaszczyzną od której nasąpiło odbicie a wiązką ugięta

Kąt ugięcia 20 między wiązką ugięta a wiązką przechodzącą

Długość fali promieniowania zależy od materiału, z którego zbudowana jest anoda aparatu rentg. są to Co,Cu,Fe

Met		
Lauego Obr. M DSH	Zmienne Stałe Stałe	Stały Zmienny zmienny

  const. (promieniowanie monokrystaliczne)

  const. (promieniowanie polikrystaliczne)

23. Doświadczenie Fridricha-Knippinga (1912) wg pomysłu Lauego.

Rozpatrywana jest dyfrakcja promieni rentgenowskich na prostej sieciowej, przy założeniach:

1)atomy w krysztale ułożone są wg schematu sieci krystalicznej

2)atomy są nieruchome

3)promieniowanie rentgenowskie uginane jest przez z atomów, czynnikiem rozpraszającym są E

4)wszystkie elektrony danego atomu skupiają się w jednym punkcie

Aby nastąpiło interferencyjne wzmocnienie promieni rozproszonych, różnica dróg miedzy promieniami rozproszonymi na sąsiednich węzłach prostej sieciowej musi być całkowitą wielokrotnością długości fali S=n Równanie Lauego określa kierunek rozchodzenia się wzmocnionego promienia interferencyjnego w przypadku ugięcia promieni rentg. na prostej sieciowej,

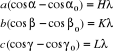
H,K,L określają rząd interferencji

24. Metoda obracanego kryształu

W tej metodzie wiązka II promieni monochromatycznych pada na niewielki monokryształ ustawiony na główce goniometrycznej, który jest obracany z prędkością 0,2-2obr/min . Kryształ jest obracany jest po to, aby coraz to nowe płaszczyzny sieciowe kryształu w różnych odległościach d(hkl) mogły znaleźć się pod kątem połysku (w pozycji odbijającej) w stosunku do wiązki padającej promieni. Rentgenogramy wykonane tą metoda noszą nazwę dyfraktogramów warstwicowych.

25.Metoda Bragga

Chodzi to o zjawisko powstawania wzmocnionego promieniowania odbitego od płaszczyzn sieciowych (hkl). Warunek: Odbite od kolejnych płaszczyzn sieciowych promienie ulęgają wzmocnieniu gdy różnica dróg promieni odbitych od dowolnych dwóch II płaszczyzn jest całkowitą wielokrotnością długości fali S=n. n =2d(hkl)*sinV V-kąt odbłysku równanie to określa kierunek rozchodzenia się wzmocnionego promieniowania rentg. Refleksy to ślady wiązek promieni rentg. odbitych od płaszczyzn sieciowych.

26. Metoda proszkowa Debay'a-Scherrera i Hulla (1916) i (1917)

W tej metodzie wiązka II promieni monochromatycznych pada na preparat sporządzony z krystalicznego proszku. Sproszkowanie kryształu ma na celu ustawienie różnych płaszczyzn sieciowych krystalitów w pozycjach odbijających (taka sama rola jak obrót kryształu w met. obracanego monokryształu). Obraz dyfrakcyjny preparatu rejestruje się na błonie fotograficznej zwiniętej w walec umieszczonej współosiowo z preparatem lub na płaskiej błonie ustawionej prostopadle do wiązki promieni padających.

27. Równoważność teorii Lauego i Bragga.

Interpretacja dyfraktogramu za pomocą równania Bragga jest całkowicie równoważna rozwiązaniu układu trzech równań Lauego, przy czym każdemu refleksowi odpowiada jeden układ równań o trzech liczbach hkl charakteryzujących refleks.

29. Wsaźniokowanie

wysokość piku, intensywność,  , d(hkl),hkl, a0

30. Zastosowanie analityczne i strukturalne rentgenografii

Metody te znajdują zastosowanie w chemii, fizyce, metalurgii, geologii i są podstawa tzw. Rentgenografii stosowanej.

1)jakościowe i ilościowe określenie składu fazowego substancji 2)wyznaczenie granic fazowych 3)precyzyjne pomiary stałych sieciowych 4)wyznaczanie rozmiarów krystalitów 5)wyznaczanie współczynników rozszerzalności 6)badanie naprężeń wewnętrznych

31. PRAWA KRYSTALOGRAFII

Prawo stałości typu - substancja zdefiniowana pod względem fizycznym i chemicznym ma zawsze taki sam typ sieci niezależnie od sposobu otrzymania próbki.

Prawo równoległości - naturalne ściany zew. kryształu są zawsze równoległe do płaszczyzn sieciowych, a krawędzie kryształu do prostych sieciowych.

Prawo stałości kątów - kąty między analogicznymi ścianami zmierzone na różnych egzemplarzach kryształu są takie same (stałe).

Prawo wymiernych wskaźników (Millera) - naturalne ściany kryształów znajdujące się w równowadze termodynamicznej z otoczeniem mają zawsze wskaźniki całkowite i niewielkie.

32. Klasyfikacja struktur Goldschimdta :struktury homo- i heterodesmiczne Jeżeli atomy, z których zbudowane są kryształy, znajdują się w takim samym (lub co najmniej w zbliżonym) stanie to różne typy struktur można połączyć w jedną grupę struktur porównywalnych. Jeżeli natomiast atomy znajdują się w różnych stanach to typy struktur krystalicznych należą do grup nieporównywalnych. Różnych stanów Goldschmidt wyróżnił trzy : atomowy, jonowy, metaliczny (zwracał jednak także uwagę na istnienie stanów pośrednich, przejściowych pomiędzy tymi skrajnymi). Hipoteza Goldschimdta : każda grupa struktur porównywalnych jest scharakteryzowana przez wspólny dla grupy stan jednego lub kilku elementów budowy kryształu. W strukturach porównywalnych rozmiary elementów wspólnych (atomów, jonów) są w przybliżeniu stałe, nawet jeżeli zmienia się ich otoczenie (koordynacja). Tak więc podstawą podziału struktur nie jest geometryczne podobieństwo budowy, lecz chemiczne podobieństwo stanów w jakich znajdują się atomy, jako elementy struktury.

Struktury homodesmiczne - struktury o jednym typie wiązań (jednorodnym) np.: NaCl, diament,

Struktury heterodesmiczne - struktury, w których elementy połączone są za pomocą wiązań dwóch lub więcej rodzajów np.:lód

Kryształ rośnie najwolniej w kierunku równoległym do słabych wiązań, a pęka najłatwiej w kierunku do nich prostopadłym.

33.Wiązania chemiczne w kryształach

Wiązanie chemiczne w krysztale tym różni się od innych wiązań, iż niektóre molekuły (np.:NaCl, MgO ) nie tworzą wiązań. Takim zapisem posługujemy się tylko po to by podać proporcję w jakich się łączą molekuły (podajemy skład chem. kryształu ). Wiązania chemiczne dzielimy na: skierowane (możemy mówić o grupie atomów ze sobą połączonych) i nieskierowane (oparte na oddziaływaniach kolumbowskich). Występuje tylko jedno wiązanie chemiczne, które występuje w różnych stopniach polaryzacji i delokalizacji.

Różnice energetyczne: wiązanie atomowe 100-150 kcal/mol ; w. jonowe 50-100 kcal/mol; w. metaliczne 0-50 kcal/mol.

Wiązanie atomowe poprzez proces delokalizacji może przejść w metaliczne, natomiast poprzez proces polaryzacji w jonowe.

34. Kryształy jonowe

Gdy para elektronów należy tylko do jednego atomu to mamy do czynienia z wiązaniem jonowym (nie ma 100% wiązania jonowego). Para elektronów jest bliżej pierwiastka, który jest bardziej elektroujemny. Wiązanie jonowe występuje wtedy gdy mamy do czynienia z atomami, które znacznie różnią się elektroujemnością. Za wiązanie jonowe uważamy wiązanie, które jest w co najmniej 50% spolaryzowane. Jony - sztywne kule obdarzone ładunkiem, który zachowuje się tak jakby był w środku kuli. Ładunek wytwarza wokół siebie pole sił, gdyż działa on na pewna odległość. Rozmiar tego pola jest określony promieniem jonowym. Kule te nie polaryzują się 9zawsze są kulkami, nie zmieniają kształtu). Każdy kation dąży do otoczenia się maksymalną liczbą anionów, czyli do minimalizacji energii potencjalnej, a co za tym idzie do maksymalizacji liczby koordynacyjnej. Jony tworząc naroża wielościanu foremnego zapewniają minimum oddziaływania między sobą, wypełniają więc obszar jak najlepiej (gęste upakowanie).

Promień jonowy jest to tzw. promień sfery nieprzenikalności jonu, odległość między jonami jest sumą promieni jonowych kationu i anionu. Sposoby obliczania promieni jonowych wg metod: Lande, Paulinga, Goldschmidta, Ahrensa.

Liczba koordynacyjna - mówi nam ile jonów innego znaku otacza nasz jon, zależy ona od stosunku rk/ra, Mamy następujące liczby koordynacyjne 2,3(trójkąt),4(czworościan),6,8,12

Wytrzymałość wiązania jonowego to stosunek ładunku formalnego do liczby koordynacyjnej W = z/Lk ; z - wynika z liczby elektronów walencyjnych, ładunek formalny; Zf ładunek efektywny, Zr - ładunek faktyczny.

REGUŁY PAULINGA - reguły struktur jonowych

1)Reguła koordynacji - W kryształach jonowych każdy kation jest otoczony anionami tak, że tworzą one naroża wielościanu foremnego, odległość kation-anion jest suma promieni kationu i anionu, liczba koordynacyjna zależy od stosunku rk/ra

2)Reguła elektroobojętności - w strukturach jonowych ładunek anionu jest wysycony dokładnie lub niemal dokładnie przez wytrzymałość wiązań otaczających go kationów

3)Reguła wspólnych naroży - wielościany koordynacyjne powinny łączyć się wspólnymi narożami, rzadziej krawędziami, a najrzadziej ścianami. Chodzi tu o to aby połączenie gwarantowało jak największą odległość miedzy kationami.

4)Reguła mocnych kationów - jeżeli w strukturach jonowych występują kationy, których wytrzymałość wiązania jest bardzo duża to nie mają one miedzy sobą wspólnych naroży

5)Reguła oszczędności - jeżeli dany jon tworzy różne wielościany to nie występują one jednocześnie w jednej strukturze, a jeżeli już ma to miejsce to jeden z rodzajów anionów zdecydowanie przeważa.

Podział struktur jonowych:

1)izodesmiczne WA-B < ½ [Za] - ozn. to ze nie możemy powiedzieć czy jakiś kation jest związany mocniej lub słabiej z anionem np.: NaCl

2)anizodesmiczne WA-B > ½ [Za] - np.: jeden kation jest bardziej związany z anionem niż pozostałe.

3)mezodesmiczne WA-B = ½ [Za] - np.: Na4[SiO4] Krzem ma dokładnie ½ ładunku tlenu, najchetniej tlenem podzieliłyby się swa krzemy

Struktury typu AB

-halogenki Li- , Na-, K- , Rb -

-tlenki MgO, CaO, SiO, BaO , NaO, FeO

-siarczki MgS, CaS, MnS, PbS, (piryt FeS)

Związki mające tę samą strukturę krystaliczną noszą nazwę izotypowych.

Struktury typu AB2

-tlenki TiO2, SnO2, WO2,PbO2,SiO2, ZrO2(ma najwyższą możliwą symetrię Fm3m regularny)

-fluorki MgF2,NiF2,CoF2, FeF2,MnF2

Struktury A2B3

- hematyt Fe2O3 R3c romboedryczny

- korund Al2O3 R3c - romboedryczny (jeśli dodamy Cr powstanie rubin)

STRUKTURY HETERODESMICZNE:

- struktura typu perowsklitu (sumaryczny ładunek A i B musi być równy 6) ABO3

A1+B5+ - LiNbO3, NaNbO3, KnbO3, KTaO3,

A2+B4+ - CaTiO3, SrTiO3, BaZrO3, BaTiO3, MgSiO3

A3+B+3 - LaCrO3, YalO3, LaAlO3

- struktura typu spinelu (AB2O4): MgAl2O4, FeAl2O4, FeCr2O4,MgSiO4

- gibsyt Al(OH)3 wiązanie typu Al.-O i jony protonowe P2/c jednoskośny

- kalcyt CaCo3 R3c romboedryczny (między jonami Ca występują struktury CO3)

- apatyt Ca3(PO4)2 P63/m heksagonalny

- gips CaSo4*2H2O C2/c jednoskośny

35. Krzemiany

Kryterium systematyki Krzemianów

1)Rodzaj anionu krzemotlenowego

2)Grupa przestrzenna symetrii

3)Skład chemiczny

Kształt anionu krzemotlenowego wyznacza nam grupy systematyczne krzemianów:

1)Monokrzemiany 2)Oligokrzemiany 3)Krzemiany łańcuchowe4)warstwowe5)szkieletowe

Polikondensacja to przyłączanie się krzemianów do siebie

36.Kryształy metaliczne

Wiązanie metaliczne polega na posiadaniu elektronów zdelokalizowanych, siły działające pomiędzy węzłami sieci to oddziaływania kolumbowskie. W metalach mamy do czynienia z 1 lub 2 elektronami walencyjnymi. Elektron spełnia tu rolę anionu. Elektron to cząstka elementarna czyli w stosunku do rozmiaru kationu możemy traktować go jako punkt. Węzłami krystalicznej sieci metalu są kationy „pływające w morzu elektronów”. Wiązania II(pi) będące blisko siebie mogą tworzyć razem wiązanie zdelokalizowane. Występują tu więc dwa typy wiązania: to co w metalu i molekularne. Struktury metali są to struktury gęstego ułożenia kul w przestrzeni. Wszystkie atomy tworzące tu strukturę maja te same rozmiary. Wypełnienie naprawdę gęsto to upakowanie 74% przestrzeni. Istnieją dwa sposoby upakowania (close packing): I)trzecia warstwa jest dokładnie taka sama jak pierwsza, a więc sześciokąt, te możliwość nazywamy heksagonalnym upakowaniem (aba,aba), komórka elementarną dla hcp jest komórka elementarna centrowana na podstawach. II)trzecia warstwa jest podobna do drugiej obrócona o 60° , te możliwość nazywamy regularnym upakowaniem (abc,abc,abc), komórka elementarna dla takiego upakowania(ccp) jest komórka centrowana na wszystkich ścianach. III)Trzecią istniejąca strukturą (ale nie tak gęsto upakowaną, jednak jej bliska) jest bcc (body centered cell). Pierwiastki mające rozmiary promieni zbliżone do siebie mogą podmieniać sobie atomy, mogą się ze sobą mieszać tworzą w ten sposób stopy.. Stopy metali są to roztwory stałe atomów [roztwór stały - wyodrębniona faza zawierająca co najmniej dwa składniki, przy czym jej typ sieci przestrzennej jest identyczny z typem sieci jednego ze składników (rozpuszczalnika, osnowy), a parametry sieci (a,b,c,,,γ) są ciągłą funkcją składu chemicznego]. Struktury mogą powstawać w następujące sposób: 1) podmieniamy kuleczki innego koloru, ale struktura jest zachowana. Nazywamy ją struktura substytucyjną. 2) Pomiędzy kulki wkładamy inne atomy (dużo mniejsze od osnowy).Struktura ta nosi nazwę intersticjalną (międzywęzłową). Roztwory międzywęzłowe to roztwory gdzie w miejsca pomiędzy węzłami wstawiamy atom, jednak jego rozmiar musi być bardzo mały np.: Fe z C -stal 3) Nadmiar składnika A wynika z niepełnego obsadzenia pozycji B, czyli występują luki. Te strukturę nazywamy substrakcyjną. Od sposobu uporządkowania zalezą właściwości stopu. Gdy zmieszamy Cu I Au w proporcjach 1:1 to mamy gęste upakowanie, struktura jest poukładana, ale wtedy nie wiemy, który atom jest który. Inna możliwość to struktura uporządkowania , czyli układają się warstwami AuCuAuCu. Układ krystalograficzny jest ten sam, ale symetria jest inna, tak jest np.: przy innych proporcjach

37. Kryształy kowalencyjne

Węgiel występuje w trzech podstawowych formach :

- diament (występuje jako minerał, wyszlifowany diament to brylant) to naturalnie wyst. odmiana węgla, grupa symetrii Fd3m, komórkę elementarna tworzy 8 atomów, w strukturze diamentu występują wyłącznie wiązania kowalencyjne 9atomowe). Atomy w diamencie są ściśle ze sobą związane. Diament jest twardy i posiada wysoka temp. Topnienia (należy topić go bez dostępu tlenu, aby się nie spalił), jest przeźroczystym izolatorem

- grafit (struktura heterodesmiczna - jako wiązanie chem. występuje wiązanie atomowe, jako fizyczne - wiązanie van der Wallsa) Posiada strukturę heksagonalna C6/m mc. Atomy połączone są wiązaniem atomowym tylko w płaszczyźnie, czwarty elektron tworzy słabe wiązanie van der Wallsa pomiędzy warstwami. Grafit jest miekki, używamy go jako smar, przewodzi prąd elektryczny. Różnice między diamentem i grafitem wynikają ze struktury i rodzaju występujących wiązań

- fuleren (struktura heterodesmiczna), człony fulerenu sa pierścieniami benzenowymi (co drugie wiązanie jest wiązaniem podwójnym). Fuleren powstaje przez kombinację członów pięcio- i szeęcioatomowych. W zależności od liczby koordynacyjnej poszczególnych członów otrzymujemy różne kształty „brył” fulerenu np.: C60. Jeżeli zerwiemy podwójne wiązanie to możemy przyłączyć inny pierwiastek np.: H,OH-, O2,R itd. Fulereny ulegają polimeryzacji.

- węgiel amorficzny (nie ma uporządkowania dalekiego zasięgu stąd nie jest ona kryształem).

Związki ORGANICZNE

Struktury tych związków są heterodesmiczne. Kształt cząsteczki:

Kulisty, wrzecionowaty, płytkowaty.

Nie ma wiązań kowalencyjnych, są za to jonowe, dipolowe, van der Waalsa.

Stany mezomorficzne nazywane są ciekłymi kryształami, sa to stany częściowego uporządkowania w jednym z warunków w przestrzeni ( lub w dwóch wymiarach).

38.Stan szklisty

1)Definicja fenomenologiczna - substancja szklista ma wszystkie właściwości fizyczne anizotropowe, w przeciwieństwie do kryształów, które maja właściwości fizyczne anizotropowe tzn. zależą od kierunku, w którym badamy. Kryształ nie rozbija się przypadkowo, szkło zawsze.

2) Definicja amorficzna - stan szklisty jest substancja amorficzną (bezpostaciową) przyjmuję kształt naczynia, w którym zastygła, natomiast kryształ krystalizuje w ściśle określonych formach (np.: kwarc w słupach heksagonalnych, kształt ten wynika z klasy symetrii kryształu).

3) Definicja genetyczna (Maxwella) - Szkło to stan materii, który powstaje z fazy ciekłej osiągając lepkość 10¹³ płaza [Pu].

Temp. witryfikacji - temp. Zeszklenia, zależy ona od szybkości chłodzenia, jeśli chłodzenie przebiega szybko to temp. Witryfikacji jest wysoka

4) Definicja termodynamiczna - stan szklisty w przeciwieństwie do stanu krystalicznego nie jest w stanie równowagi termodynamicznej. Stan metatrwały - lokalne minimum energii. Szkło jest stanem zatrzymanym w procesie krystalizacji (prędzej czy później szkło musi zamienić się w stan szklisty, jednak na wykrystalizowanie często potrzeba bardzo długiego okresu czasu).

5) Definicja strukturalna - w szkle nie ma uporządkowania dalekiego zasięgu, a więc nie znajdziemy tam periodu identyczności, czyli nie istnieje sieć krystaliczna w szkle, co za tym idzie nie otrzymamy refleksów na rentgenogramie.

Temperatury charakterystyczne (od lewej do prawej na wykresie T/T) :

Tg -zeszklenia; Tnukl - zarodkowania fazy krystalicznej w fazie szklistej ; Tm - mięknięcia - szkło ma lepkość mniejszą od 10¹³ płaza [Pu] ; Tkr - krystalizacji; Tpol - przemiany polimorficznej; Tf - topnienia.

Im odległość miedzy Tg i Tf jest większa tym łatwiej substancje zamienić w szkło.

Substancje dzielimy na: nieszkłotwórcze (np.: NaCl lepkość 0,0159 Pu) oraz szkło twórcze, czyli te, które w temp. Topnienia mają dużą lepkość (np.: v-SiO2 w pobliżu temp. Topnienia ma lepkość 10 Pu.

Każdą substancję można zamienić w stan szklisty, pozostaje tylko kwestia skali trudności tej przemiany.

STRUKTURA SZKŁA - wyróżnia się dwie koncepcje:

I) teoria krystalitowa - struktura szkła dotyczy kilku cząsteczek bezładnie ułożonych między sobą (uporządkowanie bliskiego zasięgu). Pomiędzy małymi elementami wiązania są pozrywane.

II) teoria więźby ciągłej - nie ma żadnego porządku miedzy pierścieniami, ale wiązania nie są zerwane (struktura mikroheterogeniczna )

---