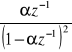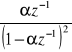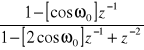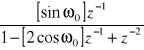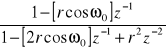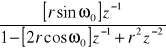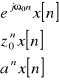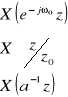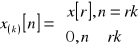Przykłady par transformat Z (dwustronnych)
Lp |
Sygnał |
Transformata |
ROC |
1 |
|
1 |
Wszystkie z |
2 |
|
|
|
3 |
|
|
|
4 |
m - całkowite |
|
Wszystkie z za wyjątkiem 0, gdy m>0 lub ∞, gdy m<0 |
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
Tablica właściwości przekształcenia Z
![]()
, ![]()
, ![]()
obszar zbieżności: R R1 R2
Lp |
Właściwości |
Sygnał |
Transformata z |
ROC |
1 |
Liniowość |
|
|
Co najmniej wspólny obszar R1 i R2 |
2 |
Przesunięcie w dziedzinie czasu |
n0 - całkowite |
|
R, ewentualnie z początkiem u-du wsp, lub bez |
3 |
Skalowanie w dziedzinie z |
|
|
R
z0R
|a|R |
4 |
Odwrócenie osi czasu |
|
|
|
5 |
Ekspansja w dziedzinie czasu |
r - całkowite |
|
|
6 |
Sprzężenie |
|
|
R |
7 |
Splot |
|
|
Co najmniej wspólny obszar R1 i R2 |
8 |
Pierwsza różnica |
|
|
Co najmniej obszar wspólny R i |z|>0 |
9 |
Akumulata |
|
|
Co najmniej obszar wspólny R i |z|>1 |
10 |
Różniczkowanie w dziedzinie z |
|
|
R |
Twierdzenie o wartości początkowej: Jeżeli x[n]=0 dla n<0, to ![]()
Wyszukiwarka
Podobne podstrony:
Cw8LPCPS, Edukacja, studia, Semestr IV, Podstawy i Algorytmy Przetwarzania Sygnałów, Ćwiczenia, Cwic
Piapsy zagadnienia, Edukacja, studia, Semestr IV, Podstawy i Algorytmy Przetwarzania Sygnałów
JavaScript- podstawy, Edukacja, studia, Semestr IV, Języki Programowania Wysokiego Poziomu, Java skr
Zarzadzanie i systemy jakosci - sciaga I, STUDIA, SEMESTR IV, Podstawy zarządzania, pz, Zarzadzanie,
TECHNIKA MIKROPROCESOROWA (1), Edukacja, studia, Semestr IV, Technika Mikroprocesorowa
liniowkaWKLEPANE PYTANIA, Edukacja, studia, Semestr IV, Układy Elektroniczne
pytania na smoki, Edukacja, studia, Semestr IV, Technika Mikroprocesorowa
Układy Elektroniczne zagadnienia, Edukacja, studia, Semestr IV, Układy Elektroniczne
ASK-koło pierwsze pytania z mojej grupy, Edukacja, studia, Semestr IV, Architektura Systemów Kompute
Optoelektronika kolo 1, Edukacja, studia, Semestr IV, Optoelektronika, Pytania na koła, zestaw 8
ROBOTY, Edukacja, studia, Semestr VI, Podstawy Robotyki
ask4, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Wyklad
opracowane pytania na ASK@, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Oprac
Projekt 3, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Projekt, Projekt 3
ask1, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Wyklad
SzybkiStart, Edukacja, studia, Semestr IV, Języki Programowania Wysokiego Poziomu, Java skrypty, inn
Teoria 2003, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Opracowania pytań
LAST MINUTE mikroproce 150pytan zminimalizowane by wookie, Edukacja, studia, Semestr IV, Technika Mi
assembler 1, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Projekt, Projekt 1
więcej podobnych podstron