WYDZIAŁ NAUK TECHNICZNYCH UWM
Sprawozdanie z ćwiczeń laboratoryjnych
Kierunek			Rodzaj studiów
BUDOWNICTWO			STUDIA NIESTACJONARNE
Data	Rok studiów	Grupa		Semestr
07.04.2013	I	I		II
TEMAT ĆWICZEŃ: Wyznaczanie oporu za pomocą mostka Wheastone'a
Imię i nazwisko studenta: Damian Drężek Dmochowski Daniel
OCENA:

Zagadnienia teoretyczne

Prawo Ohma

Natężenie prądu elektrycznego płynącego przez przewodnik jest wprost proporcjonalne do wartości napięcia elektrycznego na jego końcach i odwrotnie proporcjonalne do rezystancji przewodnika.

Jednostką natężenia jest amper 1A

I prawo Kirchoffa

Suma natężeń prądów wpływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

II prawo Kirchhoffa

Suma napięć na wszystkich elementach obwodu elektrycznego jest równa napięciu źródła:

U₁ + U₂ + U₃ + ... + U_n = U_z

Opór elektryczny

Jest to stosunek napięcia do natężenia prądu. Jednostką oporu jest 1 om- Ω.

Połączenie szeregowe

Dla szeregowego połączenia n rezystorów można wyliczyć rezystancję wypadkową (opór wypadkowy), R jako sumę rezystancji składowych:

Połączenie równoległe

Dla równoległego połączenia n oporników można wyliczyć rezystancję wypadkową (opór wypadkowy), R, który jest mniejszy od najmniejszego oporu składowego:

MOSTEK WHEATSTONE'A

Dokładny pomiar oporu elektrycznego możemy przeprowadzić metodą mostka Wheatstone'a. Polega ona na porównaniu oporu nieznanego z oporem znanym. Mo- stek Wheatstone'a to układ oporów połączonych jak na rysunku.

Mostek taki składa się z dwóch równolegle połączonych rozgałęzień: ACB i ADB. W jednym rozgałęzieniu znajdują się opory R1 i R2, a w drugim Rx i R3. Oba rozgałęzienia połączone są „mostkiem CD”, w którym znajduje się czuły galwanometr G. Prąd doprowadzony do mostka rozgałęzia się w punktach A i B.

Pomiar oporu nieznanego, np. R3, sprowadza się do doprowadzenia mostka do stanu równowagi za pomocą zmiany wartości oporów znanych. Mostek jest w równo- wadze, kiedy między punktami C i D różnica potencjałów jest równa zeru, czyli przez galwanometr nie płynie prąd (IG = 0). Jeżeli między punktami C i D nie płynie prąd, to napięcie między tymi punktami musi być równe zeru, tzn. potencjały w tych punktach muszą być jednakowe. Wobec tego, między punktami A i B panuje różnica potencjałów U, która zapewnia odpowiednie spadki napięć w rozgałęzieniach. Ponieważ napięcie między punktami C i D jest równe zeru, więc spadki napięć na odcinkach AC i AD oraz CB i DB są między sobą odpowiednio równe:

V_AC= V_AD , V_CB= V_DB

Wprowadzając oznaczenia natężeń prądu płynącego w rozgałęzieniach i stosując prawo Ohma, otrzymamy równania wyrażające równość wymienionych spadków napięć

I1R1  I xRx , I2R2  I3R3

Ponieważ przez mostek CD prąd nie płynie, więc dla węzłów rozgałęzienia C i D możemy zastosować I prawo Kirchhoffa i otrzymamy równania I₁=I₂, I_X=I₃

Z tych czterech równań eliminujemy natężenie prądu i dzieląc równania stronami otrzymamy

warunek równowagi mostka

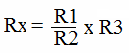
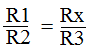
PRZEBIEG BADAŃ:

Przyrządy którymi się posługiwaliśmy:

• Źródło prądu stałego

• Mostek Wheatstone'a

• Opór wzorcowy i opory badane

• Galwanometr

• Wyłącznik

• Przewody do łączeń

WYKONANIE ĆWICZENIA

1. Zmontowaliśmy obwód według podanego schematu

2. Obserwując wskazówkę galwanometru ustawiliśmy ruchomy styk tak, aby przez galwanometr nie płyną prąd (wskazówka galwanometru w położeniu zerowym)

3. Przy danym położeniu styku kilkukrotnie włączyliśmy i wyłączyliśmy prąd w obwodzie obserwując wskazówkę galwanometru. Jeżeli wskazówka nie wychyliła się odczytaliśmy wartości l1 i l2. Pomiar powtórzyliśmy kilkukrotnie i obliczyć wartości średnie l1 i l2

4. 
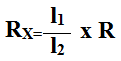
   Wartość oporu badanego obliczyliśmy ze wzoru:

5. Pomiary powtórzyliśmy dla 3 różnych oporów oraz dla układów oporów połączonych równolegle i szeregowo

6. Sprawdziliśmy zgodność wyników otrzymanych z pomiaru dla połączenia szeregowego i równoległego z wynikami otrzymanymi po zastosowaniu danych wzorów dla tych połączeń

7. Przeprowadziliśmy dyskusję błędu dla połączenia równoległego oporów

WYNIKI NASZYCH OBLICZEŃ:

	R	∆R	I1	I2	RX	∆RX
R1	15	0,15	446	554	12,075	40,26
R2	16	0,16	532	468	18,1801	62,511
R1 SZEREGOWO Z R2	17	0,17	553	447	24,875	65,16
R1 RÓWNOLEGLE Z R2	26	0,26	495	505	30,746	64,77