Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska
Fizyka dla elektroników 2
Nr ćwiczenia:	Temat:
44A	Pomiar zależności oporu metali i półprzewodników od temperatury
Termin zajęć	Prowadzący	Sprawozdanie wykonał	Ocena
Wt., 9 III 2010 Godz. 15.15-16.45	Dr inż. Ewa Oleszkiewicz	Andrzej Głowacki 163968

1. Cel ćwiczenia

Pomiar wartości oporu metali i półprzewodników w funkcji temperatury oraz wyznaczenie temperaturowego współczynnika rezystancji metalu i szerokości przerwy energetycznej półprzewodnika.

2. Spis przyrządów

• Multimetr cyfrowy METEX M-3850

• Urządzenie zawierające grzejnik, regulator temperatury, wentylator oraz badane próbki

3. Wyniki i opracowanie pomiarów

(błędy bezwzględne były przybliżane do pierwszej cyfry znaczącej w górę, o ile wstępne przybliżenie nie zmieniało ich wartości o więcej niż 10% - w przeciwnym wypadku do dwóch cyfr znaczących)

W sprawozdaniu wykonano analizę pomiarów dla próbek 1 (metal) i 4 (półprzewodnik)

1. Metal

Ogrzewanie:

Tabela 1 - Wyniki pomiarów i obliczeń dla metalu podczas ogrzewania

t [°C]	∆t [°C]	Rm [Ω]	∆Rm [Ω]	a	∆a	b [Ω]	∆b [Ω]	α [°C^-1]	∆ α [°C^-1]	[%]
30,3	±1,0	114,4	±0,7	0,3036	±0,0022	104,55	±0,15	2,904	±0,026	±0,9
35,4			115,6								±0,7
40,8			116,4								±0,7
45,2			118,4								±0,7
50,5			119,7								±0,7
55,5			121,5								±0,8
60,5			122,3								±0,8
65,2			124,2								±0,8
70,5			125,5								±0,8
75,2			127,6								±0,8
80,6			128,7								±0,8
85,4			131,0								±0,8
90,5			131,9								±0,8
95,2			134,0								±0,8
100,5			135,0								±0,8

Oznaczenia:

t - wskazana temperatura

R­­_m­ - zmierzona rezystancja metalu

a, b - współczynniki prostej postaci
, wyznaczonej metodą regresji liniowej

α - temperaturowy współczynnik rezystancji

Ochładzanie:

Tabela 2 - Wyniki pomiarów i obliczeń dla metalu podczas ochładzania

t [°C]	∆t [°C]	Rm [Ω]	∆Rm [Ω]	a	∆a	b [Ω]	∆b [Ω]	α [°C^-1]	∆ α [°C^-1]	[%]
33,5	±1,0	114,8	±0,7	0,3084	±0,0014	104,85	±0,10	2,941	±0,017	±0,6
35,0			115,6								±0,7
44,7			118,6								±0,7
50,5			120,5								±0,8
54,8			121,6								±0,8
60,2			123,7								±0,8
65,2			125,3								±0,8
70,4			126,4								±0,8
75,3			128,2								±0,8
80,4			129,9								±0,8
85,2			131,1								±0,8
90,1			133,1								±0,8
94,7			134,1								±0,8
100,5			135,0								±0,8

Wykorzystane wzory i przykładowe obliczenia:

Niepewność pomiaru rezystancji obliczona została zgodnie z niedokładnością miernika, przykładowo:

Jako, że nie była znana dokładność termometru wbudowanego w zestaw laboratoryjny, za niepewność pomiaru temperatury przyjęto typową dla termometrów cyfrowych niedokładność równą ±1,0 °C.

Współczynniki prostej postaci
wyznaczone zostały na podstawie punktów pomiarowych metodą regresji liniowej. W tym celu wykorzystano następujące wzory:

,
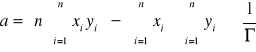
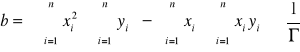
, gdzie:

n - liczba punktów pomiarowych, x_i - i-ty pomiar temperatury, y_i - i-ty pomiar rezystancji, oraz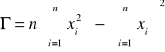
. Niepewności współczynników a i b obliczone zostały następująco:
,
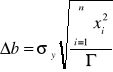
, gdzie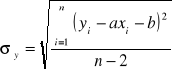
.

Dla metalu zachodzi równość
, zatem
,
. Temperaturowy współczynnik rezystancji wyznaczyć więc można jako:
. Przykładowo dla ochładzania:
.

Niepewność pomiarową temperaturowego współczynnika rezystancji wyznaczono metodą różniczki zupełnej: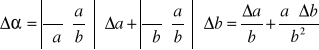
. Przykładowo dla ochładzania:
.

Względna niepewność pomiaru współczynnika:

Przedstawienie wyników na wykresach:

2. Półprzewodnik

Ogrzewanie:

Tabela 3 - Wyniki pomiarów i obliczeń dla półprzewodnika podczas ogrzewania

t [°C]	∆t [°C]	T [K]	∆T [K]	1000/T [K^-1]	∆(1000/T) [K^-1]	Rs [Ω]	∆Rs [Ω]	lnRs	∆lnRs	A [K]	∆A [K]
30,3		±1,0		303,45	±1,0	3,295	±0,011	99,5	±0,7			4,6002	±0,0071	2,461	±0,021
35,4				308,75		3,239	±0,011	91,8	±0,7			4,520	±0,008
40,8				313,85		3,186	±0,011	80,6	±0,7			4,389	±0,009
45,2				318,55		3,139	±0,010	71,3	±0,7			4,267	±0,010
50,5				323,25		3,094	±0,010	62,7	±0,7			4,138	±0,011
55,5				328,75		3,042	±0,010	58,5	±0,8			4,069	±0,014
60,5				333,35		3,000	±0,009	51,3	±0,8			3,938	±0,016
65,2				338,55		2,954	±0,009	47,2	±0,8			3,854	±0,017
70,5				343,35		2,912	±0,009	41,3	±0,8			3,72	±0,02
75,2				348,55		2,869	±0,009	38,2	±0,8			3,643	±0,021
80,6				353,35		2,830	±0,008	33,4	±0,8			3,509	±0,024
85,4				358,55		2,789	±0,008	30,5	±0,8			3,418	±0,026
90,5				363,25		2,753	±0,008	27,0	±0,8			3,30	±0,03
95,2				368,45		2,714	±0,008	24,9	±0,8			3,215	±0,032
100,5				373,35		2,678	±0,008	21,9	±0,8			3,09	±0,04

Tabela 4 - Ostateczne wyniki obliczeń dla półprzewodnika (ogrzewanie)

A [K]	∆A [K]	Eg		∆Eg
				[J]	[eV]	[J]	[eV]
2,461	±0,021	6,80	0,424	±0,06	±0,004

Oznaczenia:

t - wskazana temperatura

T - temperatura w Kelwinach

R­­_s­ - zmierzona rezystancja półprzewodnika

A - nachylenie prostej postaci
, wyznaczonej metodą regresji liniowej

E­_g - wyznaczona przerwa energetyczna półprzewodnika

Ochładzanie:

Tabela 5 - Wyniki pomiarów i obliczeń dla półprzewodnika podczas ochładzania

t [°C]	∆t [°C]	T [K]	∆T [K]	1000/T [K^-1]	∆(1000/T) [K^-1]	Rs [Ω]	∆Rs [Ω]	lnRs	∆lnRs	A [K]	∆A [K]
33,5		±1,0		306,65	±1,0	3,261	±0,011	89,7	±0,7			4,496	±0,008	2,4972	±0,0025
35,0				308,15		3,245	±0,011	86,5	±0,7			4,4601	±0,0081
45,0				318,15		3,143	±0,010	66,2	±0,7			4,193	±0,011
50,2				323,35		3,093	±0,010	58,5	±0,7			4,069	±0,012
55,3				328,45		3,045	±0,010	51,7	±0,7			3,945	±0,014
59,2				332,35		3,0089	±0,0091	47,0	±0,8			3,85	±0,02
65,2				338,35		2,956	±0,009	41,8	±0,8			3,73	±0,02
70,4				343,55		2,911	±0,009	36,7	±0,8			3,603	±0,022
75,3				348,45		2,870	±0,009	33,9	±0,8			3,523	±0,024
80,4				353,55		2,828	±0,008	30,7	±0,8			3,424	±0,026
85,2				358,35		2,791	±0,008	27,5	±0,8			3,314	±0,030
90,1				363,25		2,753	±0,008	24,5	±0,8			3,199	±0,033
94,7				367,85		2,718	±0,008	22,2	±0,8			3,100	±0,036
100,2				373,35		2,6785	±0,0072	21,9	±0,8			3,086	±0,037

Tabela 6 - Ostateczne wyniki obliczeń dla półprzewodnika (ochładzanie)

A [K]	∆A [K]	Eg		∆Eg
				[J]	[eV]	[J]	[eV]
2,4972	±0,0025	6,895	0,4304	±0,007	±0,0005

Wykorzystane wzory i przykładowe obliczenia:

Niepewności pomiarów temperatury i rezystancji zostały wyznaczone tak samo jak dla metalu. Temperatura na Kelwiny została przeliczona wg zależności:
. Niepewność wyrażona w Kelwinach pozostała taka sama.

Niepewność po przeliczeniu skali temperatury (
) wyznaczona została w następujący sposób: „w górę” jako
, oraz „w dół”
. Obie wartości były bardzo zbliżone, więc jako ostateczną niepewność przyjęto większą z nich.

Przykładowo dla ochładzania:

Ostatecznie więc
.

Podobną metodą wyznaczona została niepewność po przeliczeniu skali rezystancji:

,
(jako ostateczna większa z nich). Przykładowo dla ochładzania:

Ostatecznie:

Nachylenie A prostej postaci
, wyznaczone zostało w analogiczny sposób jak dla metalu (metodą regresji liniowej)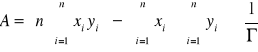
, przy czym w tym wypadku x_i oznacza i-tą wartość postaci
, natomiast y_i i-tą wartość postaci
. Również niepewność nachylenia prostej została wyznaczona w analogiczny sposób jak dla metalu.

Dla półprzewodników w zakresie badanych temperatur zależność rezystancji od temperatury jest postaci: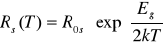
, logarytmując obie strony otrzymamy:
(k - stała Boltzmanna). Zatem wyznaczone nachylenie prostej równe jest:
. Przerwę energetyczną badanego półprzewodnika wyznaczyć więc można jako:
, co wyrazić można w eV:
.

Przykładowo dla ogrzewania:

oraz w przeliczeniu na eV:
.

Niepewność pomiaru przerwy energetycznej wyznaczona została metodą różniczki zupełnej:
. Przykładowo dla procesu ogrzewania:

Przedstawienie wyników na wykresach:

4. Wnioski

Otrzymana dla badanej próbki metalu wartość temperaturowego współczynnika rezystancji jest nieco mniejsza niż dla miedzi czy złota (dla miedzi wynosi ok.
, natomiast dla złota
), wynik jest jednak prawidłowego rzędu. Również wartość wyznaczonej przerwy energetycznej badanej próbki półprzewodnika jest z zakresu dopuszczalnych dla półprzewodników wartości. W obu wypadkach wyniki otrzymane dla ogrzewania i ochładzania są bardzo zbliżone i biorąc pod uwagę wyznaczone niepewności są niesprzeczne. Niewielkie różnice wynikać mogą z dynamicznych zmian temperatury (szczególnie w początkowych fazach ogrzewania i ochładzania), które sprawiały pewne trudności pomiarowe. Wyznaczone charakterystyki (dla metalu
, dla półprzewodnika
) są wyraźnie liniowe, punkty pomiarowe niewiele odbiegają od prostych wyznaczonych metodą regresji liniowej - to z kolei przełożyło na niewielkie niepewności współczynników wyznaczonych prostych, a więc również ostatecznych wyników. Warto również zauważyć, że niedokładności przyrządów pomiarowych nie miały wpływu na niepewności ostatecznych wyników - wpływ na to miało jedynie rozproszenie punktów pomiarowych względem aproksymowanych prostych.

1

---