WYTRZYMALOSC MATERIAŁÓW SEM 2:
Schemat obliczeniowy konstrukcji budowlanej:
- materiał użyty na konstrukcję (stal, beton, drewno)
- geometria konstrukcji (pręt, rama, powłoka)
- więzy (posadowienie i kontakt z innymi konstrukcjami)
- obciążenia
Założenia dotyczące materiału:
- ciało jest tzw. continuum materialnym (każdy punkt
geometryczny ciała ma przypisaną masę, która jest
rozłożona w sposób ciągły w objętości konstrukcji)
- materiał jest jednorodny (ma takie same własności w
każdym punkcie) i izotropowy (własności nie zależą od
wyboru kierunku)
- materiał można opisać za pomocą równań i stałych
występujących w tych równaniach (najprostszy opis materiału za pomocą funkcji algebraicznych, niezależnych od czasu i spełniających założenie o liniowej sprężystości).
Założenia dotyczące geometrii: (3 typy konstrukcji):
- konstrukcje prętowe (mają 2 wymiary opisujące przekrój znacznie mniejsze od trzeciego, czyli długości)
- konstrukcje powierzchniowe (mają 2 wymiary opisujące powierzchnię znacznie większe od trzeciego, czyli grubości
- konstrukcje masywne posiadają wszystkie 3 wymiary tego samego rzędu
- konstrukcje prętowe - belki, ramy, łuki, kratownice
Założenia dotyczące więzów:
podpory (przegubowe, przegubowo-przesuwne, zamocowania)
posadowienia (bezpośrednie, na palach)
połączenia (niepodatne - spawane, podatne - na śruby zwykłe)
Założenia dotyczące obciążeń:
Rodzaje obciążeń:
obciążenia powierzchniowe:
skupione [kN] lub rozłożone [kN/m2]
obciążenia objętościowe (siły masowe)
Inny podział:
obciążenia stałe
obciążenia zmienne:
a) ruchome (pojazdy) lub nieruchome (np. działania klimatyczne)
b) statyczne (prędkość energii kinetycznej jest równa zero)
lub dynamiczne
Obliczeniowe zasady w wytrzymałości materiałów:
- zasada zesztywnienia - Jeśli konstrukcja deformuje się nieznacznie, to przy obliczaniu reakcji i sił wewnętrznych możemy założyć, że konstrukcja w położeniu równowagi ma konfigurację wyjściową (inaczej: wpływ przemieszczeń na obliczanie reakcji i sił wewnętrznych jest pomijalnie mały)
- zasada superpozycji-
- zasada de Saint Venanta
SIŁA WEWNETRZNA-Siłą wewnętrzną nazywamy funkcję wektorową dwóch wektorów , która określa wypadkową sił międzycząsteczkowych, z jakimi wszystkie punkty materialne części II, wyznaczone płaszczyzną ၰ o normalnej zewnętrznej
działają na punkt materialny leżący na płaszczyźnie ၰ, o promieniu wodzącym i przyporządkowany części I
TWIERDZENIE O UKŁADZIE SIŁ WEWNETRZNYCH I ZEWNETRZNYCH- Układ sił wewnętrznych przyłożonych do punktów materialnych leżących na płaszczyźnie podziału o normalnej jest równoważny układowi sił zewnętrznych przyłożonych do odciętej, drugiej części bryły.
TWIERDZENIE O UKLADACH ROWNOWAŻONYCH- Jeżeli dwa układy są równoważne, to sumy obu układów są równe i równe są momenty obu układów liczone względem tego samego punktu
(WI)Ⴚ (ZII) Ⴎ ,
(WII)Ⴚ (ZII) Ⴎ
Oś pręta - miejsce geometryczne punktów, będących środkami ciężkości przekrojów pręta dowolnymi płaszczyznami przecinającymi jego tworzące
Przekrój poprzeczny - przekrój płaszczyzną prostopadłą do osi pręta
Biegun redukcji - punkt leżący na płaszczyźnie przekroju i należący do osi pręta (środek ciężkości przekroju poprzecznego)
SIŁY PRZEKROJOWE- Siłami przekrojowymi przyłożonymi do przekroju poprzecznego, o wersorze normalnej zewnętrznej , nazywać będziemy składowe zredukowanego do środka ciężkości przekroju poprzecznego, układu sił zewnętrznych przyłożonych do drugiej części przeciętej bryły, odniesione do lokalnego układu współrzędnych.
Funkcje sił przekrojowych - punkty i przedziały charakterystyczne:
Punkty charakterystyczne to:
- początek i koniec pręta
- punkty przyłożenia sił i momentów skupionych
- początek i koniec obciążenia ciągłego
- punkty, w których pochodna funkcji opisującej oś pręta jest nieciągła
Przedziałem charakterystycznym nazywamy odcinek pręta zawarty pomiędzy dwoma sąsiednimi punktami charakterystycznymi.
Belką nazywamy układ prętów o osiach prostoliniowych połączonych pomiędzy sobą sztywno lub przegubowo, tak jednak, że wszystkie osie leżą na jednej prostej.
Obciążenie belki stanowi dowolny układ sił.
Belką prostą nazywamy pręt prostoliniowy jednoprzęsłowy, przewieszony (długość pręta większa od odległości podpór) lub nie, dowolnie obciążony
Ramą nazywamy układ prętów prostoliniowych połączonych w sposób sztywny, nie leżących na jednej prostej i dowolnie obciążonej, np.:
Łukiem nazywamy konstrukcję złożoną z jednego lub więcej prętów krzywoliniowych
Kratownicą nazywamy konstrukcję złożoną z prętów prostych połączonych pomiędzy sobą w węzłach będących idealnymi przegubami, do której obciążenie zewnętrzne oraz więzy przyłożone są wyłącznie w węzłach.
Tw. o zredukowanym układzie sił wewnętrznych w przekrojach poprzecznych prętów kratownicy - Układ sił wewnętrznych w przekroju każdego pręta kratownicy redukuje się tylko do siły osiowej Fx(x)
TWIERDZENIA O PRETACH ZEROWYCH
Tw. 1 o prętach zerowych (pręty w których siła podłużna Fx=0):
Jeśli kratownica poddana obciążeniu układem sił zewnętrznych (Z)Ⴚ(0) pozostaje w równowadze, to układ sił działający na każdy wycięty węzeł jest układem równoważnym układowi zerowemu
Tw. 2.: Jeśli w węźle schodzą się dwa pręty i węzeł jest nieobciążony siłą zewnętrzną to siły przekrojowe w obu prętach są równe zero N1 = N2 = 0
Tw. 3: Jeśli w węźle schodzą się dwa pręty i węzeł jest obciążony siłą zewnętrzną równoległą do jednego z nich to w drugim pręcie siła przekrojowa jest równa zero (N2 = 0)
Tw. 4: Jeśli w węźle schodzą się trzy pręty, z których dwa są równoległe i węzeł nie jest obciążony siłą zewnętrzną to siła przekrojowa w pręcie trzecim jest równa zeru (N2 =0)
Metoda Rittera
- metoda przecięć przez max 3 pręty, z wykorzystaniem tw. o równowadze układu sił zewnętrznych i wewnętrznych przyłożonych do jednej części kratownicy
Metoda analityczna równoważenia węzłów
- Sposób polega na wykorzystaniu warunków równowagi dla każdego i - tego węzła z osobna:
ၓXi = 0; ၓZi = 0
CHARAKTERYSTYKI GEOMETRYCZNE FIGUR PŁASKICH:
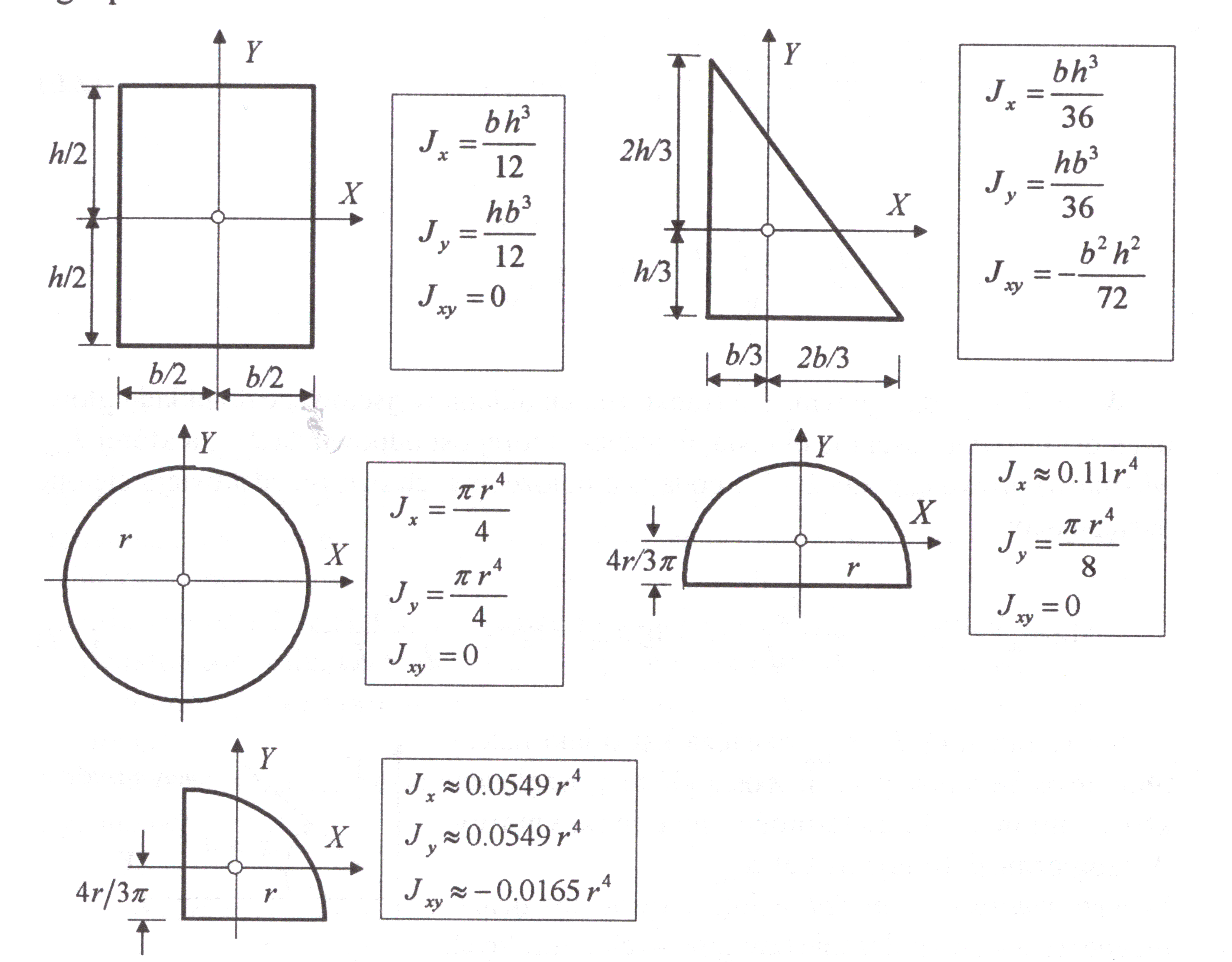
POLE FIGURY- A
MOMENT STATYCZNY-Sx = A yc, Sy = A xc,
MOMENT BEZWŁADNOSCI-
WSKAŹNIK WYTRZYMAŁOŚCI-
PROMIEŃ BEZWŁADNOŚCI-
PROMIEŃ PRZEKROJU-
STAN NAPRĘŻENIA I ODKSZTAŁCENIA W PUNKCIE:
Definicja naprężenia (gęstość sił wewnętrznych):
Naprężeniem w punkcie o wektorze wodzącym r na powierzchni
przekroju o normalnej v nazywamy wektor:
Macierz naprężeń w punkcie:
- uporządkowany zbiór współrzędnych trzech wektorów naprężeń
na płaszczyznach prostopadłych do osi układu współrzędnych.
Stany odkształcenia w punkcie: nieskończony zbiór odkształceń liniowych i kątowych wszystkich włókien przechodzących przez ten punkt
Rodzaje stanu odkształcenia:
- jednoosiowy
- płaski
- przestrzenny
Odkształcenia liniowe i kątowe główne- Odkształcenia główne w danym punkcie to ekstremalne wartości odkształceń liniowych w nim występujących. Są to odkształcenia
liniowe dwóch do siebie prostopadłych włókien, których odkształcenia kątowe są równe zeru.
RÓWNIANIA FIZYCZNE HOOKA:
Zasada superpozycji- Skutek w określonym kierunku, wywołany prze zespół przyczyn
działających równocześnie, jest równy algebraicznej sumie
skutków wywołanych w tym kierunku przez każdą z przyczyn
działających oddzielnie.
- Warunek proporcjonalności
- Warunek niezależności działania
OSIOWE ROZCIAGANIE I SCISKANIE
Zasada de Saint-Venanta:
Jeśli na niewielki obszar ciała będącego w równowadze działają rozmaicie rozmieszczone, ale statycznie równoważne obciążenia, to w odległości znacznie przekraczającej wymiary tego obszaru wywołują one jednakowe stany naprężenia i odkształcenia.
Zasada analogii formalnej Mohra:
Kąt ugięcia w dowolnym punkcie belki rzeczywistej równa się sile poprzecznej w tym samym punkcie belki fikcyjnej, czyli ၪ(x) = Qf(x)
2. Ugięcie w dowolnym punkcie belki rzeczywistej równe momentowi zginającemu w tym samym punkcie belki fikcyjnej, czyli w(x) = Mf(x)
Analiza stanu naprężenia i odkształcenia
położenie osi obojętnej nie zależy od wartości siły N
oś obojętna nie przechodzi przez środek ciężkości przekroju, a odcinki jakie odcina na osiach układu współrzędnych znajdują się w ćwiartce po przeciwnej stronie punktu przy łożenia siły
położenie osi obojętnej zależy od współrzędnych punktu przyłożenia siły i geometrii przekroju poprzecznego
Naprężenia normalne w - przekroju mimośrodowo rozciąganym lub ściskanym - będą miały ten sam znak wtedy i tylko wtedy gdy oś obojętna będzie leżała poza przekrojem pręta lub będzie styczna do niego.
Miejsce geometryczne punktów przekroju pręta, w których siła podłużna wywołuje naprężenia normalne jednego znaku nazywamy rdzeniem przekroju.
ENERGIA SPTRĘŻYSTA:
Energią sprężystą U nazywamy pracę sił wewnętrznych na odkształceniach przez nie wywołanych:
U = L = W = Wp
L - praca
W - energia wewnętrzna układu
Wp - energia potencjalna
U Ⴎ energia odwracalna (po usunięciu sił obciążających jest zużyta na odzyskanie początkowej konfiguracji ciała)
Gęstość energii sprężystej ၆ (energia sprężysta właściwa) jest to ilość energii sprężystej na jednostkę objętości ciała
HIPOTEZY WYTĘŻENIOWE:
Warunek bezpieczeństwa:
W Ⴃ WN
gdzie
W - miara wytężenia np. W = ၳ
WN - wartość graniczna wytężenia np. WN = fy
Stany bezpieczne opisuje przedział na osi
ၳ <- fy, + fy>
W przestrzennym stanie naprężenia Ⴎ Ⴅ wiele stanów ၳ może prowadzić do przekroczenia fy stąd Ⴎ hipotezy wytężeniowe, wskazujące przypadek miarodajny.
Podstawowy cel hipotez wytężeniowych - to przekształcenie przestrzennego stanu naprężenia do hipotetycznego stanu jednoosiowego: Tၳ Ⴎ ၳhipot.= ၳz Ⴃ fy
HIPOTEZA WYTEZENIA GELIUSZA:
O wytężeniu materiału w danym punkcie ciała decyduje wartość maksymalnego DODATNIEGO naprężenia głównego, niezależnie od rodzaju stanu naprężenia, czyli
WG = ၳz = max (ၳს1ჱ, ၳს2ჱ, ၳს3ჱ)
gdzie ს…ჱ - nawias Macauleya:
ၳსiჱ = ၳi dla ၳi > 0
ၳსiჱ = 0 dla ၳi Ⴃ 0
Warunek bezpieczeństwa wg Galileusza ma postać:
ၳz = max (ၳს1ჱ, ၳს2ჱ, ၳს3ჱ) Ⴃ fy,
czyli
ၳს1ჱ Ⴃ fy, ၳს2ჱ Ⴃ fy, ၳს3ჱ Ⴃ fy,
HIPOTEZA WYTĘŻENIOWA RANKINE`A - CLEBSCHA:
O wytężeniu materiału w danym punkcie ciała decyduje wartość BEZWZGLĘDNA maksymalnego naprężenia głównego, niezależnie od rodzaju stanu naprężenia, czyli
Wr-c = ၳz = max (|ၳ1 |, |ၳ2 |, |ၳ3 |)
Warunek bezpieczeństwa wg RANKINE`A - CLEBSCHA ma postać:
ၳz = max (|ၳ1|, |ၳ2|, |ၳ3|) Ⴃ fy,
czyli
|ၳ1 | Ⴃ fy Ⴎ - fy Ⴃ ၳ1 Ⴃ fy
|ၳ2 | Ⴃ fy Ⴎ - fy Ⴃ ၳ2 Ⴃ fy
|ၳ3 | Ⴃ fy Ⴎ - fy Ⴃ ၳ3 Ⴃ fy
HIPOTEZA WYTĘŻENIOWA COULOMBA-TRESCI-GUESTA:
O wytężeniu materiału w danym punkcie ciała decyduje wartość bezwzględna ekstremalnych naprężeń STYCZNYCH, niezależnie od rodzaju stanu naprężenia, czyli
WC-T-G = max [|0,5(ၳ1- ၳ2)|, |0,5(ၳ1 -ၳ3)|, | 0,5(ၳ2 -ၳ3) |]
Warunek bezpieczeństwa wg C-T-G ma postać:
max [|0,5(ၳ1- ၳ2)|, |0,5(ၳ1 -ၳ3)|, |0,5(ၳ2 -ၳ3) |] Ⴃ 0,5 fy,
czyli
|0,5(ၳ1 - ၳ2) | Ⴃ 0,5 fy Ⴎ - fy Ⴃ ၳ1 - ၳ2 Ⴃ fy
|0,5(ၳ1 - ၳ3) | Ⴃ 0,5 fy Ⴎ - fy Ⴃ ၳ1 - ၳ3 Ⴃ fy
|0,5(ၳ2 - ၳ3) | Ⴃ 0,5 fy Ⴎ - fy Ⴃ ၳ2 - ၳ3 Ⴃ fy
HIPOTEZA WYTĘŻENIOWA HUBERA-MISESA-HENCKY`EGO
O wytężeniu materiału w danym punkcie ciała decyduje gęstość energii odkształcenia postaciowego, niezależnie od rodzaju stanu naprężenia, czyli
WH-M-H = ၆f = [(ၳ1- ၳ2)2, (ၳ2 - ၳ3)2, (ၳ3 - ၳ1)2](1+ ၮ)/6E
Warunek bezpieczeństwa wg C-T-G ma postać:
[(ၳ1- ၳ2)2, (ၳ2 - ၳ3)2, (ၳ3 - ၳ1)2](1+ ၮ)/6E Ⴃ (fy)2(1+ ၮ)/3E
lub po przekształceniach
5
![]()
![]()
![]()
![]()
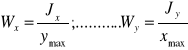
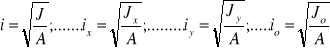
![]()
![]()
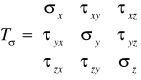
![]()
![]()
Wyszukiwarka
Podobne podstrony:
5915
5915
5915
5915
więcej podobnych podstron