I Pracownia Zakładu Fizyki PL |
|||
Nazwisko Płaska Anna i imię |
Wydział Elektryczny Grupa ED.2.6. |
||
Data 2 III wyk. Ćwicz. 1998
|
Numer 1. ćwiczenia |
Temat Wyznaczanie prędkości fali głosowej metodą rezonansu. |
|
Zaliczenie
|
Ocena |
Data |
Podpis |
Wyznaczanie prędkości fali dźwiękowej metodą rezonansu.
W słupie powietrza znajdującym się w rurze zamkniętej z jednej strony , można wywołać drgania własne , odpowiadające
fali stojącej . Węzeł fali powstaje przy zamkniętym końcu rury , strzałka przy otwartym . Można to osiągnąć zbliżając widełki kamertonu do pionowo ustawionej rury wypełnionej częściowo wodą . Kamerton stanie się źródłem fali biegnącej, która ulegnie odbiciu o powierzchnię wody . Dobierając odpowiednio długość słupa powietrza można osiągnąć rezonans fali biegnącej i odbitej . Maksymalne natężenie dźwięku świadczy o uzyskaniu maksymalnej amplitudy drgań słupa powietrza .
1. 2.
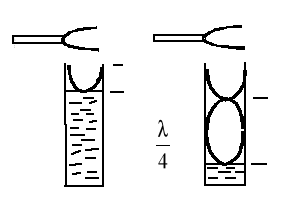
Rysunek przedstawia sytuację kiedy mieści się w długości słupa powietrza (1.) tylko 1/4 długości fali (węzeł fali stojącej przy powierzchni wody , strzałka przy wylocie rury) czyli długość ta jest minimalna i (2.) 3/4 długości fali .
Będziemy badać obydwie sytuacje .
Przy założeniu , że częstotliwość drgań kamertonu jest równa częstotliwości drgań słupa powietrza i jest znana , dokonujemy pomiaru długości fali , wg poniższych wzorów .
l=(2n+1)λ/4 , gdzie n=0,1,2,3...
V=λf
V0=λf√(T0/T)
l- długość słupa powietrza
f- częstotliwość drgań kamertonu
V- prędkość fali w powietrzu w
temp. otoczenia
T- temperatura otoczenia
V0- pr. fali w temp. T0
T0=273 K (00C)
Wykonanie ćwiczenia:
Zestaw pomiarowy składa się z dwu naczyń połączonych wężykiem .
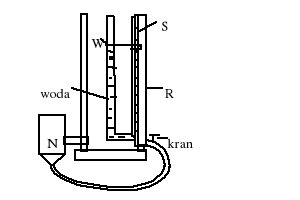
W- pionowa rura z wodą
szerokie ruchome naczynie z wodą , połączone z rurą
gumowym wężem
zawór (kran) pozwalający na regulowanie wysokości słupa
wody
S- skala z której odczytujemy wyniki pomiarów
Pomiary:
1- Nad wylotem rury mocujemy kamerton tak , aby nie dotykał jej brzegów .
Maksymalnie podnosimy poziom wody .
Uderzamy młoteczkiem w kamerton , aby wywołać falę.
Odkręcamy częściowo kranik .
Obniżamy poziom wody do momentu zaobserwowania maksymalnego wzmocnienia dźwięku , czyli pierwszego maksimum .
Ustalamy poziom wody i dokonujemy pomiaru .
W analogiczny sposób wykonujemy jeszcze 9 pomiarów , których wyniki umieszczamy w tabeli .
Przechodzimy do drugiego maksimum czyli pomiaru długości słupa powietrza w którym zmieści się 3/4 długości fali .
Poziom wody ustalamy na nieco niższy , odkręcamy kranik i postępując w analogiczny sposób szukamy drugiego maksimum.
Wyniki pomiarów umieszczamy w tabeli:
lp.
|
l1 10-3m |
l2 103m |
l1śr 10-3m |
l2śr 10-3m |
f 1/s |
T K |
T0 K |
V0śr m/s |
ri(l1) 10-3m |
ri(l2) 10-3m |
ri2(l1) 10-6m |
ri2(l2) 10-6m |
∑ri2 (l1) |
∑ri2 ( l2) |
δr(l1) 10-3m |
δr(l2) 10-3m |
δrśrl1 10-3m |
δrśrl2 10-3m |
δV0 m/s |
V=V0śr+ -3δV0śr |
|
1. |
175 |
568 |
172.8 |
567.5 |
440 |
298 |
273 |
332.4 |
2.2 |
0.5 |
4.48 |
0.25 |
11.6 |
8.5 |
1.14 |
0.97 |
0.36 |
0.31 |
0.4 |
332.4+-1.2 |
|
2. |
173 |
567 |
|
|
|
|
|
|
0.2 |
-0.5 |
0.04 |
0.25 |
|
|
|
|
|
|
|
|
|
3. |
174 |
566 |
|
|
|
|
|
|
1.2 |
-1.5 |
1.44 |
2.25 |
|
|
|
|
|
|
|
|
|
4. |
172 |
568 |
|
|
|
|
|
|
-0.8 |
0.5 |
0.64 |
0.25 |
|
|
|
|
|
|
|
|
|
5. |
174 |
568 |
|
|
|
|
|
|
1.2 |
0.5 |
1.44 |
0.25 |
|
|
|
|
|
|
|
|
|
6. |
172 |
569 |
|
|
|
|
|
|
-0.8 |
1.5 |
0.64 |
2.25 |
|
|
|
|
|
|
|
|
|
7. |
172 |
566 |
|
|
|
|
|
|
-0.8 |
-1.5 |
0.64 |
2.25 |
|
|
|
|
|
|
|
|
|
8. |
172 |
567 |
|
|
|
|
|
|
-0.8 |
-0.5 |
0.64 |
0.25 |
|
|
|
|
|
|
|
|
|
9. |
172 |
568 |
|
|
|
|
|
|
-0.8 |
0.5 |
0.64 |
0.25 |
|
|
|
|
|
|
|
|
|
10. |
172 |
568 |
|
|
|
|
|
|
-0.8 |
0.5 |
0.64 |
0.25 |
|
|
|
|
|
|
|
|
|
Dyskusja błędu pomiaru:
l1=1/4λ - długość słupa powietrza (1.)
l2=3/4λ - długość słupa powietrza (2.)
l1śr - wartość średnia (średnia arytmetyczna pomiaru)
l2śr - wartość średnia
f - częstotliwość drgań kamertonu
T - temperatura otoczenia
T0=273 K - temperatura w warunkach normalnych
V0śr - prędkość dźwięku w warunkach normalnych (odczytana z tablic)
ri(l1)=l1-l1śr - błąd pozorny pomiaru
ri(l2)=l2-l2śr - błąd pozorny pomiaru
ri(li)<3δr(li) - warunek , który gwarantuje uniknięcie błędu grubego dla kryterium trzysigmowego
ri2(l1)= ri(l1)*ri(l1)
ri2(l2)= ri(l2)*ri(l2)
σ - odchylenie standardowe
σr(l1)=*[*i=110 ri2(l1)]/n-1 - błąd pozorny
σr(l2)=*[*i=110 ri2(l2)]/n-1
σrśrl1 =σr(l1)/*n - błąd bezpośredni
σrśrl2 =σr(l2)/*n
σV0śr=[(δV0śr/δl1śr)2(σr(l1))2+(δV0śr/δl2śr)2(σr(l2))2 ]1/2
względny błąd pomiaru
V=V0śr+-3δV0śr - wartość prędkości dźwięku otrzymana
z pomiarów
Wnioski:
W warunkach pracowni fizycznej można dokonać pomiaru
długości fali dźwięku z dosyć dużą dokładnością, wykorzystując proste zależności i wzory. Możliwe jest również dość precyzyjne oszacowanie popełnionego błędu .