Estymacja przedziałowa
Model 1 (δ znane)
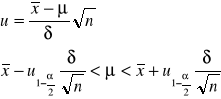
![]()
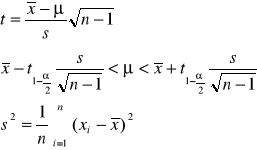
Model 2 (δ i μ nie znane)
Estymacja przedziałowa wariancji
Model 1 (n małe)
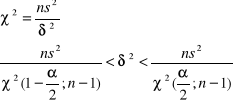
Model 2 (n>50)
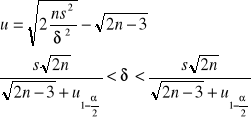
Hipotezy dotyczące wartości przeciętnych
HO: μ= μ0
![]()
Model 1 (δ znane)
μ<μ0 , to ukr=u(α)
μ>μ0 , to ukr=u(1-α)
μ≠μ0 , to ukr1=u(α/2) ukr2=u(1-α/2)
Model 2 (δ i μ nie znane)
![]()
μ<μ0 , to tkr=t(α , n-1)
μ>μ0 , to tkr=t(1-α , n-1)
μ≠μ0 , to tkr1=t(α/2 , n-1) tkr2=t(1-α/2 , n-1)
Model 3 (δ i μ nie znane, a n duże)
Hipotezy dotyczące 2 wartości średnich
Model 1 (δ1 i δ2 znane)
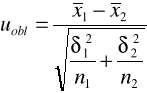
Model 2 (δ1 i δ2 nieznane)
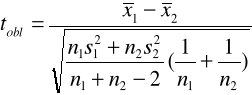
Model 3 (n duże)
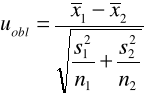
Test dla wariancji populacji generalnej
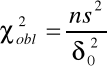
δ2< δ02 to χ2kr= χ2(α , n-1)
Estymacja - Wzory
1
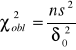
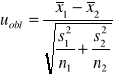
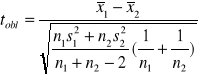
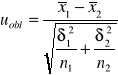
![]()
![]()
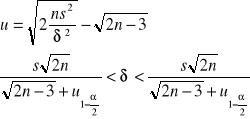
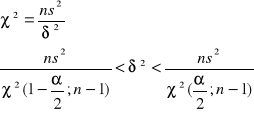
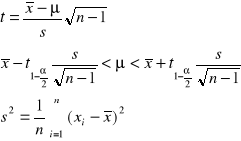
![]()
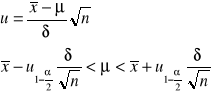
Wyszukiwarka
Podobne podstrony:
estymacja wzory, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Parametry stosowane w statystyce opisowej, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Analiza regresji między dwiema zmiennymi, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Korelacje rang - ściąga, Płyta farmacja Bydgoszcz, statystyka, pozostałe
SWD, Płyta farmacja Bydgoszcz, statystyka, pozostałe
(2461) stat mat 01, Płyta farmacja Bydgoszcz, statystyka, pozostałe
analiza szeregu czasowy, Płyta farmacja Bydgoszcz, statystyka, pozostałe
miary zmienosci, Płyta farmacja Bydgoszcz, statystyka, pozostałe
regresja, Płyta farmacja Bydgoszcz, statystyka, pozostałe
korelacja, Płyta farmacja Bydgoszcz, statystyka, pozostałe
miary, Płyta farmacja Bydgoszcz, statystyka, pozostałe
siłakorelacji, Płyta farmacja Bydgoszcz, statystyka, pozostałe
więcej podobnych podstron