Zadanie 2: Wyznaczyć zbiór tych 
dla których szereg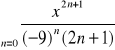 
jest zbieżny (ustalić także rodzaj zbieżności). Podać promień zbieżności tego szeregu oraz obliczyć jego sumę wewnątrz przedziału zbieżności.
|
Zadanie 2: Wyznaczyć zbiór tych
dla których szereg
jest zbieżny (ustalić także rodzaj zbieżności). Podać promień zbieżności tego szeregu oraz obliczyć jego sumę wewnątrz przedziału zbieżności.
Rozwiązanie:
Ustalenie zbieżności szeregu:
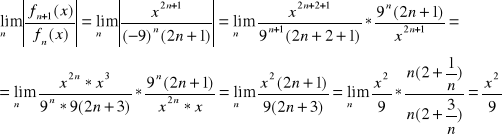
Szereg jest zbieżny dla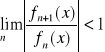 
wtedy:
Dla 
szereg jest bezwzględnie zbieżny, a dla 
szereg jest rozbieżny.
Ustalamy zbieżność na krańcach przedziału
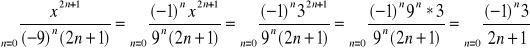
Szereg naprzemienny 
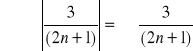
szereg naprzemienny nie jest bezwzględnie zbieżny, sprawdzam więc zbieżność z kryterium Leibnitza
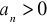
ciąg malejący
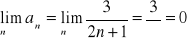
Wniosek szereg jest zbieżny warunkowo dla 
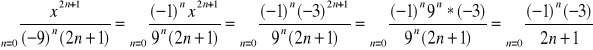
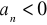
ciąg rosnący
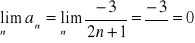
Wniosek szereg jest zbieżny warunkowo dla 
Podsumowując szereg jest zbieżny w przedziale 
i rozbieżny w przedziale 
Obliczenie promienia zbieżności
Promień zbieżności wynosi 
, dla 
co możemy odczytać z przedziału w którym szereg jest zbieżny 
Obliczenie sumy szeregu w przedziale zbieżności
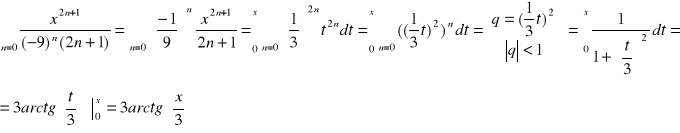
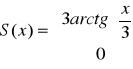
Obliczenie sumy na krańcach szeregu
Odpowiedź: Dla 
szereg jest bezwzględnie zbieżny, dla 
warunkowo zbieżny, a dla 
szereg jest rozbieżny, promień zbieżności wynosi 
a suma szeregu jest równa 
dla 
, 0 dla 
, 
dla 
i 
dla 
.
Autor: Anna B. grupa 2