Model matematyczny podsystemu silnika
W przyjętym modelu opartym na średnich parametrów obiegu podsystem silnika traktowany jest jako objętość, którą tworzy układ komór roboczych cylindrów, o znanych charakterystykach. Do analitycznego opisu tych charakterystyk użyto równań regresji aproksymujących wyniki pomiarów otrzymanych podczas badań identyfikacyjnych silnika SW-680. Przeprowadzona analiza uzyskanych charakterystyk pozwoliła ustalić związek między wskaźnikami pracy silnika, które w decydujący sposób określają warunki współpracy silnika z turbosprężarkowym zespołem doładowującym oraz podstawowe właściwości silnika takie jak moc, zużycie paliwa, trwałość. Do wskaźników tych należą przede wszystkim: temperatura spalin w układzie wylotowym przed turbiną - Tt, która decydując o mocy turbiny spalinowej określa parametry doładowania silnika, sprawność cieplna - ηc, współczynnik napełnienia - ηv oraz średnie ciśnienie tarcia - ptr, których znajomość pozwoli na wyznaczenie efektywnych wskaźników pracy silnika. Wskaźniki te zdefiniowano jako wielkości wyjściowe, których wartości mogą być obliczone lub stanowić wyniki bezpośrednich pomiarów zależnych od wartości wielkości wejściowych: prędkości obrotowej wału korbowego silnika - n, współczynnika nadmiaru powietrza - λ, ciśnienia doładowania - pd, temperatury doładowania - Td. Współzależności występujące między poszczególnymi wskaźnikami można przedstawić w postaci następujących relacji:
ηc = f(n, λ, pd, Td,) (1)
ηv = f(n, λ, pd, Td,) (?)
Tt = f(n, λ, pd, Td,) (?)
ptr = f(n) lub ptr = f(Cśr) (?)
W świetle wcześniejszych badań własnych [określenie granicznej dawki…] oraz wyników badań dostępnych w literaturze [?????], tak sformułowane zależności odzwierciedlają rzeczywiste relacje przyczynowo-skutkowe pomiędzy przedstawionymi parametrami i stanowią jakościowy model matematyczny opisujący silnik z wymaganą dokładnością. Z analizy współzależności między parametrami pracy silnika wynika, że wartości ηc, ηv, Tt w istotny sposób zależą również od kąta wyprzedzenia wtrysku paliwa. Jednakże ze względu na przyjętą w założeniach stałą optymalną regulację silnika kąt wyprzedzenia wtrysku pozostaje niezmienny i nie jest uwzględniany. Nie wyklucza to jednak możliwości wykorzystania kąta wyprzedzenia w charakterze dodatkowej wielkości wejściowej.
Opis matematyczny zależności (1), (2), (?), (?) przedstawiono w postaci wielomianów, które będąc formę zapisu funkcji aproksymacyjnych wymagających znajomości wyników badań doświadczalnych, stanowią model matematyczny silnika. Identyfikacja współczynników wielomianów wymagała rejestracji szeregu dodatkowych parametrów pracy silnika:
ciśnienia spalin przed turbiną - pt,
temperatury spalin przed turbiną - Tt,
ilości powietrza przepływającego przez sprężarki Gs,
sekundowego zużycia paliwa - Ge,
mocy użytecznej - Ne,
Rejestracja tych wielkości pozwoliła na obliczenie, korzystając ze znanych wzorów z teorii silników, wartości wyjść - sprawności cieplnej ηc, współczynnika napełnienia ηv oraz współczynnika nadmiaru powietrza λ występującego w zależnościach (/), (?), (?) w charakterze wielkości wejściowej.
Ze względu na nieliniowość charakterystyk silnika wyniki pomiarów określające współzależności między wskaźnikami dla zależności (/), (?), (?) aproksymowano, z założoną dokładnością przy przyjętym współczynniku ufności (0,95), wielomianami drugiego stopnia z współdziałaniami pierwszego rzędu o postaci:
Równania regresji opisujące te charakterystyki mają ogólną postać:
![]()
![]()
(3)
Opis zależności (?) ograniczono do wielomianu pierwszego stopnia o postaci:
![]()
(?)
Uwzględnienie wyższych stopni wielomianu nie znajdowało uzasadnienia w świetle znanych m.in. z literatury [????? Wisłocki doktorat str. 85] wyników badań. Współczynniki wielomianów wyznaczono na podstawie analizy statystycznej danych uzyskanych podczas badań doświadczalnych silnika z wykorzystaniem rachunku aproksymacyjnego. Weryfikację istotności wpływu poszczególnych składników wielomianu przeprowadzono na drodze analizy niedokładności, wariancji S2 oraz zastosowania testu t-studenta, dla przyjętej liczby stopni swobody oraz poziomu istotności ![]()
[Polański, Mańczak].
Dopasowanie funkcji do wyników pomiarów oceniano na podstawie powszechnie stosowanych statystyk: współczynnika korelacji wielowymiarowej R oraz współczynnika wariancji resztkowej S2 zakładając, że wariancja błędów została określona na podstawie 5-krotnych powtórzeń pomiarów w wybranych punktach charakterystyki silnika.
W przyjętym modelu parametry ηc, ηv, Tt, ptr są wielkościami losowymi, których wartość wyznaczona została z prawdopodobieństwem określonym przyjętym współczynnikiem ufności ![]()
, a funkcje (??) opisująca ich przebieg wyznaczone została na podstawie wartości średnich obliczonych na podstawie 5-krotnych pomiarów zbiorów wartości wielkości wejściowych n, pd, Td, λ.
Adekwatność tak uzyskanych funkcji silnika do wyników pomiarów ogranicza się jedynie do badanego obszaru. Wartości ηc, ηv, Tt dla dowolnego punktu pracy obliczane są bezpośrednio z funkcji wielomianowej (?), nie mogą więc wychodzić poza przyjęte zakresy dopuszczalnych wartości. Przyjęto następujące zakresy wejść:
![]()
; min-1
![]()
; MPa
![]()
; K
![]()
Ponadto konieczne jest uwzględnianie skojarzeń wejść, które nie mogą stać w sprzeczności z przebiegiem fizycznych zjawisk zachodzących w silniku. Dotyczy to w szczególności silnika z turbodoładowaniem, w którym ciśnienie oraz temperatura doładowania wzrastają wraz ze zwiększaniem obrotów silnika. Oznacza to, że przy stałej regulacji silnika lub założonym przebiegu momentu obrotowego ciśnienie doładowania przy minimalnej prędkości obrotowej z przyjętego zakresu, zawsze będzie niższe niż przy prędkości maksymalnej. Ekstrapolacja modelu (funkcji silnika) przez przyjęcie wartości ciśnień doładowania znacznie wykraczających poza obszar objęty warunkami doświadczalnymi mogła by prowadzić do znacznych nieścisłości. Stąd też dodatkowo przyjęto ograniczenia dotyczące maksymalnych wartości ciśnień doładowania dla minimalnej oraz maksymalnej prędkości obrotowej wału korbowego z dopuszczalnego zakresu. Pozwoli to uniknąć sytuacji, w których obliczone wg (??) wartości ηc, ηv, Tt mogłyby przyjmować niedopuszczalne wartości.
Obliczenia efektywnych wskaźników pracy silnika
Bieżące wartości momentu obrotowego Mo, mocy Ne rozwijanej przez silnik oraz jednostkowego zużycia paliwa ge obliczane są ze znanych zależności:
![]()
(??)
![]()
(??)
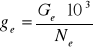
(??)
Do ich obliczenia konieczne jest wyznaczenie średniego ciśnienia indykowanego pi. Wymaga identyfikacji oporów mechanicznych silnika. Związek pomiędzy średnim ciśnieniem użytecznym pe a średnim ciśnieniem indykowanym pi określa zależność:
![]()
(??)
Wielkość ptr występujące we wzorze (??) określa się jako średnie ciśnienie tarcia, które stanowi stratę średniego ciśnienia indykowanego odpowiadającą stratom mechanicznym silnika. Dla określonego silnika średnie ciśnienie tarcia zależne jest przede wszystkim od właściwości układu tłokowo-korbowego i łożyskowania. Stąd też wyznacza się je zwykle z zależności liniowej od obrotów wału korbowego (??) [wisłocki str 72, Wajand i inni], dla której wartości współczynników b0 i b1 można określić w oparciu o analizę charakterystyk obciążeniowych silnika wg metody Willansa [?? Wisłocki 72, wajand], wykorzystując ich przybliżoną liniowość w zakresie małych obciążeń. Sposób ten ilustruje rysunek ???
Rys. 19. Sposób wyznaczania wartości średniego ciśnienia tarcia pt silnika w oparciu o charakterystykę obciążeniową godzinowego zużycia paliwa
W oparciu o metodę linii Willansa, dokonana została aproksymacja poszczególnych charakterystyk obciążeniowych silnika SW 680 i uzyskany został ich opis w postaci:
![]()
(??)
Wartości ptr obliczone z równania ![]()
dla poszczególnych prędkości obrotowych aproksymowano zależnością (??), dla której wyznaczone zostały współczynniki wielomianu o postaci:
![]()
(??)
Badania korelacyjne zależności (??) wskazały wysoki stopień korelacji dla przyjętego opisu liniowego, dla którego współczynnik korelacji wynosi R=???? a wariancja resztkowa S2=????.
Przedstawione w pracy [Wisłocki-dokt] wyniki badań korelacyjnych wskazują na niewielkie rozbieżności zależności ![]()
dla silników o zbliżonej konstrukcji. Według cytowanego autora pozwala to stwierdzić, że funkcja ![]()
jest przypisana do danego silnika i nie jest w sposób istotny zależna od charakterystyki doładowania co oznacza, że zachowuje ona swoją ważność w obliczeniach modelowych tego samego silnika z różnymi turbosprężarkami. Przeprowadzone jednak porównanie zależności ![]()
dla silnika SW680 w wersji wolnossącej oraz doładowanej pozwala stwierdzić, że ciśnienie doładowania może w istotny sposób wpływać na opory mechaniczne silnika. W pracy [33 poz. 12] wpływ doładowania na zwiększenie oporów mechanicznych proponuje się uwzględnić za pomocą członu ![]()
, gdzie f =0,1 - doświadczalnie określony wykładnik. Wtedy średnie ciśnienie tarcia silnika doładowanego wyniesie:
![]()
(??)
Ponadto w silnikach z turbodoładowaniem w obliczeniach dotyczących wymiany ładunku należy dokonać oceny wpływu umieszczenia turbiny spalinowej dławiącej wypływ spalin na warunki wymiany ładunku. Z tego względu przyjęto, że średnie ciśnienie indykowane można traktować jako sumę wartości średniego ciśnienia ![]()
odniesionej do górnej pętli wykresu obiegu (sprężanie-rozprężanie) i średniego ciśnienia wymiany ładunku pwym.
![]()
(??)
Jak zaleca szereg autorów [Portnow, i inni], średnie ciśnienie wymiany ładunku może być wyznaczone z zależności:
![]()
(??)
Dokonując odpowiednich przekształceń dla silnika doładowanego:
![]()
(??)
Równanie to po wprowadzeniu szeregu empirycznych zależności pozwala na wyznaczenie średniego ciśnienia wymiany ładunku w silniku turbodoładowanym dla znanych wartości pd i wynikających z warunków pracy turbiny wartości ![]()
.
W przyjętym modelu parametry turbiny obliczane są na podstawie ciśnienia oraz temperatury spiętrzenia spalin. Do obliczenia średniego ciśnienia wymiany ładunku, które uwzględnia obecność turbiny spalinowej umieszczonej w układzie wylotowym silnika zwiększającej opory przepływu, wykorzystano zależność [33 poz. 12]:
![]()
(??)
W równaniu tym funkcja gazodynamiczna ![]()
umożliwia przeliczenie ciśnienia spiętrzenia ![]()
wynikającego z warunków pracy turbiny na ciśnienie statyczne spalin psp w przekroju kontrolnym przed turbiną, które określa warunki przepływu ładunku przez zawór wylotowy.
Zatem:
![]()
(??)
gdzie: ![]()
Podczas wstępnej oceny wpływu turbodoładowania na wskaźniki pracy silnika przedstawionej m.in pracach [Niewiarowski, 105], średnie ciśnienie indykowane pi wyznaczane jest w sposób analityczny dla obiegu z doprowadzaniem ciepła przy stałej objętości i przy stałym ciśnieniu. Tak obliczoną wartość należy jednak traktować jako orientacyjną, nie zapewniającą dostatecznej dokładności obliczeń przy bardziej szczegółowej analizie. Średnie ciśnienie indykowane może być również obliczone ze znanej zależności:
![]()
(??)
Po odpowiednich przekształceniach uwzględniając równanie (??) można otrzymać średnie ciśnienie indykowane odniesione do górnej pętli wykresu indykatorowego można obliczyć z zależności:
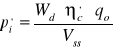
(??)
w której dawka paliwa qo przypadająca na obieg silnika wynosi:
![]()
(??)
Pewnych problemów może jednak nastręczać wyznaczenie sprawności cieplnej ![]()
odniesionej do górnej pętli wykresu. W pracach [Portnov (20 poz.4), Wanszejdt] ![]()
proponuje się wyznaczać w oparciu o empiryczną formułę, która dla określonego systemu spalania silnika przy założonym współczynniku nadmiaru powietrza (w zakresie ![]()
), uzależnia sprawność cieplną od prędkości obrotowej silnika. Konieczne jest przy tym wyznaczenie indykowanego zużycia paliwa gi podczas badań identyfikacyjnych silnika.
Przedstawione w pracy [Wisłocki-doktorat] wyniki badań korelacyjnych dla wybranej grupy silników wskazują, że przy takim założeniu dla przyjętego opisu aproksymacyjnego prawdopodobieństwo popełnienia błędu oszacowania sprawności cieplnej wynosić może 10%. Wydaje się zatem, że opis sprawności cieplnej w postaci zależności funkcyjnej od prędkości obrotowej jest zbyt dużym uproszczeniem. Przedstawione w rozdziale ??? dla wyniki pomiarów zadymienia spalin doładowanego silnika SW-680 wskazują, że przy stałym nadmiarze powietrza, temperatura oraz ciśnienie doładowania w istotny sposób wpływa na proces tworzenia mieszaniny palnej oraz jej spalania. Sugeruje to celowość uwzględnienia tych czynników w opisie sprawności cieplnej silnika. W modelu sprawność cieplną wyznaczono w oparciu o eksperymentalną zależność (??) jako funkcję aproksymująca wyniki pomiarów w postaci wielomianu:
![]()
![]()
(3)
Sprawność cieplna występująca w równaniu (??) obliczana jest na podstawie uśrednionych pomiarów mocy oraz zużycia paliwa wykonanych podczas badań na hamowni. Uwzględniono również wyniki badań identyfikacyjnych dla wyznaczenia średniego ciśnienia tarcia. Uwzględniając powyższe, wartości ηc obliczono z zależności:
![]()
(??)
Średnie ciśnienie użyteczne pe występujące w zależności (??) wyznaczono z równania:
![]()
(??)
Dopasowanie funkcji do wyników pomiarów oceniane na podstawie współczynnika korelacji wielowymiarowej R oraz współczynnika wariancji resztkowej S2 wskazuje, że dla założonego poziomu istotności ![]()
przyjęta postać wielomianu drugiego stopnia wykazuje wysoki stopień korelacji (R = ????.) oraz wariancji (S2=????).
pi =pe + ptr
pe
ptr
Ge
pe
Wyszukiwarka
Podobne podstrony:
Sprawozdanie wahado matematyczne, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
opracowanie oleje silnikowe, Studia, MECHANIKA I BUDOWA MASZYN, Płyny Eksploatacyjne
sprawozdanie techniki -Określenie składu spalin tłokowych silników spalinowych, Mechanika i Budowa M
zaliczenie odpowiedzi, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Bud
Inspiracja utworem... - referat, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mecha
Siemens, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
polimery, Politechnika Lubelska (Mechanika i Budowa Maszyn), Semestr 1, Tworzywa polimerowe
zadania z egzaminu, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Budowa
patenty1, Mechanika i budowa maszyn, Semestr VII, Ochrona patentowa
SYSTEM TOLL, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
GRUNDIG, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
termoogniwo, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
Spraw 2, Mechanika i budowa maszyn, Semestr VI, Urzadzenia elektryczne i elektroniczne w pojezdzie
Ćwiczenie nr1 - pomiar hałasu, Politechnika Lubelska (Mechanika i Budowa Maszyn), Semestr 1, Diagnos
PYTANIE 10, Mechanika i budowa maszyn, Semestr VII, Fizyka
PYTANIE 9, Mechanika i budowa maszyn, Semestr VII, Fizyka
PYTANIE 3, Mechanika i budowa maszyn, Semestr VII, Fizyka
pytania 2012-2013, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Budowa
więcej podobnych podstron