4. OBLICZANIE PRZEKŁADNI PASOWYCH

4.1. Obliczanie długości pasa i rozstawu osi

Obliczanie długości pasa i rozstawu osi kół to zagadnienia wspólne dla przekładni pasowych. Długość pasa można obliczyć z zależności jawnych przy założeniu spodziewanej odległości osi kół przekładni.

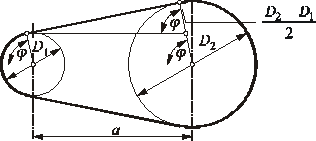
Rys. 4.1. Model geometryczny przekładni pasowej

Z zależności geometrycznych na rysunku 4.1 można wyznaczyć długość pasa według wzoru:

, (4.1)

w którym

. (4.2)

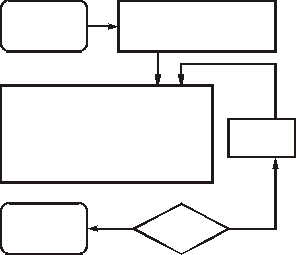
Pasy zębate lub klinowe mają określoną długość, zatem przyjmując katalogową długość pasa, należy obliczyć pasującą do niej odległość osi kół pasowych. Odległość tę można wyznaczyć tylko metodą kolejnych przybliżeń. Przykładowy algorytm takich obliczeń pokazano na rysunku 4.2. W pętli iteracyjnej tego algorytmu jest obliczana funkcja a = f(a). Pętla ta jest obiegana aż do chwili, gdy nowo obliczona wartość a będzie równa tej wartości przechowywanej w pamięci komputera z poprzedniego obiegu.

DANE: D1, D2, L
							a = a1
WYNIK: a	TAK NIE a1 = a

Rys. 4.2. Algorytm obliczania odległości osi kół przekładni pasowej

Algorytm obliczeń odległości osi jest wykorzystywany w obliczeniach przekładni zarówno z pasami klinowymi, jak i z pasem zębatym. Średnice podziałowe kół pasowych D₁ i D₂ są średnicami walców tworzonych przez osie obojętne przekrojów nawiniętego pasa.

4.2. Obliczanie przekładni z pasami klinowymi

Przekładnie z pasami klinowymi są rozpowszechnione ze względu na prostą technologię kół rowkowych oraz cichobieżność. Sposoby obliczania przekładni są ujęte w normach PN [22] i DIN [13]. Metody te, oparte na danych liczbowych odczytywanych z tablic, mogą być wykorzystane w programach komputerowych po aproksymacji liczb do postaci funkcji jawnych, tak jak to przedstawiono niżej.

Danymi wyjściowymi do obliczeń wytrzymałościowych są:

* średnice skuteczne czynnego d₁ i biernego d₂ koła pasowego,

* moc nominalna P₀ [kW] przenoszona przez przekładnię,

* prędkość obrotowa n₁ [obr/min] koła czynnego.

Moc przenoszoną przez przekładnię o z pasach określa zależność:

. (4.3)

We wzorze tym P₁ jest mocą przenoszoną przez jeden pas klinowy w przekładni z kołami o równych średnicach podczas pracy bez przeciążeń. Wartości liczbowe współczynników k_L , k_ϕ , k_i i k_T można wyznaczyć z zależności przybliżonych (opracowanych przez autora), wygodnych w obliczeniach komputerowych:

* współczynnik k_T określa wymaganą trwałość przekładni oraz stopień przeciążenia; dla przekładni obrabiarkowych przyjęto k_T = 1,25;

* współczynnik k_L zależy od długości pasa i uwzględnia częstotliwość przegięć:

, (4.4)

gdzie L₀ jest długością charakterystyczną dla rozmiaru pasa (tabl. 4.1);

* współczynnik k_ϕ zależy od kąta 2ϕ opasania małego koła (rys. 4.1) i wyraża go zależność:

; (4.5)

* współczynnik k_i zależy od przełożenia geometrycznego wyrażonego ilorazem średnic większego i mniejszego koła przekładni, którą to zależność przedstawia wzór przybliżony:

. (4.6)

Moc przenoszoną przez jeden pas klinowy określa funkcja:

[kW] , (4.7)

w której D₁ [mm] jest średnicą mniejszego koła przekładni, a prędkość pasa v [m/s] oblicza się ze wzoru:

[m/s] . (4.8)

W tablicy 4.1 zestawiono wartości współczynników stosowanych we wzorach (4.4) i (4.7), obliczone na podstawie danych z tablic liczbowych normy DIN [13].

TABLICA 4.1. Wartości liczbowe współczynników do obliczania

przekładni pasowych

Oznaczenie	Współczynniki we wzorze (4.7)			Długość L0 [mm]
pasa	c1	c2	c3	we wzorze (4.4)
HZ HA HB H20 HC H25 HD HE	0,250 0,449 0,796 1,182 1,474 1,916 3,230 4,635	7,355 19,62 50,85 95,50 143,00 214,20 507,70 953,40	0,000047 0,000076 0,000132 0,000189 0,000234 0,000295 0,000480 0,000688	1500 1700 2240 3150 3750 4500 6000 7100

Rys. 4.3. Obraz ekranu po wprowadzeniu danych do obliczeń przekładni z pasami klinowymi [9] (według przykładu na rys. 1.17 i 1.18 * wybrano paski HB)

Na rysunku 4.3 pokazano obraz ekranu po wprowadzeniu danych do programu obliczeń przekładni z pasami klinowymi. Program służy do obliczenia przekładni o kolejnych rozmiarach pasów, możliwych do przyjęcia, ze wskazaniem rozwiązań o najmniejszej ich liczbie. Spośród przypadków o równych liczbach pasów wskazuje się pasy o najmniejszym przekroju. Wartości współczynników ujęto w postaci tablic lub funkcji.

Liczba pasów jest wyznaczana ze wzoru:

(4.9)

i zaokrąglana do najbliższej (równej lub większej) liczby całkowitej.

Wynikiem obliczeń jest szkic wieńca przekładni zawierający istotne wymiary do zaprojektowania konstrukcji i technologii kół rowkowych. Na rysunku 4.4 pokazano ten wynik jako wydrukowany obraz ekranu monitora. Zawiera on także wymiary kontrolne wieńców rowkowych wykorzystywane do mierzenia średnic podziałowych kół za pomocą wałków pomiarowych.

Rys. 4.4. Wynik obliczeń przekładni z pasami klinowymi

4.3. Obliczanie przekładni z pasem zębatym

Zębate przekładnie pasowe znajdują zastosowanie w napędach obrabiarek dzięki przenoszeniu prędkości obrotowej bez poślizgu, cichobieżności oraz stosunkowo małym wymiarom w porównaniu z przekładnią z pasami klinowymi. Zgodnie z polską normą [23] oznaczenie pasa powinno zawierać kolejne dane:

a) część słowna: PAS ZĘBATY,

b) wyróżnik typu pasa: jednostronnie uzębiony * bez wyróżnika, dwustronny symetryczny * A, dwustronny naprzemianległy * B,

c) oznaczenie długości podziałowej * liczba całkowita wyrażająca długość pasa w 1/10 cala,

d) oznaczenia podziałki pasa (tabl. 4.1),

e) oznaczenie szerokości pasa * liczba całkowita wyrażająca szerokość pasa w 1/100 cala,

f) numer normy.

Na rysunkach 4.5 i 4.6 pominięto w oznaczeniach części a) i f) i pozostawiono części zgodne z ISO 5296.

Sposób obliczeń wytrzymałościowych jest opisany w polskiej normie [25]. Obliczenia te sprowadzają się do wyznaczenia mocy przenoszonej przez wstępnie zaprojektowaną przekładnię o szerokości pasa b za pomocą wzoru:

[kW] , (4.10)

gdzie v jest prędkością pasa obliczoną ze wzoru:

[m/s] . (4.11)

Współczynnik k_z we wzorze (4.10) zależy od liczby zębów małego koła pozostających w zazębieniu (kąt opasania 2ϕ  rys. 4.1) wyrażonej zależnością:

. (4.12)

Dla z_m ≥ 6 współczynnik k_z = 1 , a dla z_m < 6 wyraża się go wzorem:

. (4.13)

Pozostałe dane do wzoru (4.10) zestawiono w tablicy 4.2.

TABLICA 4.2. Charakterystyczne wielkości pasów zębatych

Oznaczenie podziałki	pb [mm]	bs0 [mm]	Ta [N]	m1 [kg/m]
MXL XL L H H XXH	2,032 5,080 9,525 12,700 22,225 31,700	6,4 9,5 25,4 76,2 101,6 127,0	27 53 245 2091 4039 7401	0,010 0,022 0,071 0,333 1,187 2,083
pb * podziałka pasa [mm], bs0 * podstawowa szerokość pasa (największa znormalizowana), Ta * dopuszczalne robocze napięcie pasa, m1 * masa 1 m pasa o szerokości bs0.

Wartości masy m₁ i T_a są zgodne z katalogiem pasów zębatych [11].

Program komputerowy do obliczania przekładni z pasem zębatym umożliwia obliczenie z powyższych wzorów minimalnych szerokości pasów zębatych, które mogą spełnić wymagania wprowadzone w postaci danych (jak na rys. 4.5).

Rys. 4.5. Obraz ekranu po wprowadzeniu danych do obliczeń przekładni z pasem

zębatym (według przykładu na rys. 1.12 i 1.13)

Wynikiem obliczeń jest propozycja przyjęcia pasa o określonej podziałce lub komunikat: nie można dobrać pasa zębatego do założonych danych.

Końcowy wynik programu w postaci graficznego obrazu ekranu przedstawiono na rysunku 4.6. Zawiera on szkice (bez zachowania proporcji wymiarów) kół pasowych, zarys wrębów i zębów kół pasowych oraz zarys narzędzia do obwiedniowej obróbki uzębień o zarysie ewolwentowym [24]. Takie przedstawienie wyników jest pomocne w opracowaniu konstrukcji i technologii kół zębatej przekładni pasowej.

Rys. 4.6. Wynik obliczeń przekładni z pasem zębatym

64

4. Obliczanie przekładni pasowych

65

65

4.2. Obliczanie przekładni z pasami klinowymi

69

4.3. Obliczanie przekładni z pasem zębatym

---