[m]

i

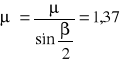
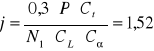
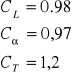
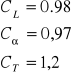
N

przedział 0,25 ≤ x₂ ≤ 0,5

przedział 0,5 ≤ x₃ ≤ 0,75

przedział 0,75 ≤ x₄ ≤ 1

Nm

przedział 0 ≤ x₁ ≤ 0,25

przedział 0,25 ≤ x₂ ≤ 0,5

przedział 0,5 ≤ x₃ ≤ 0,75

przedział 0,75 ≤ x₄ ≤ 1

1[m]	N[kN]	Ms[Nm]
0	5,1	32,47
0,25	11,9	75,76
0,5	11,9	75,76
0,75	11,9	75,76
1	5,1	32,47

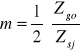
m=0,45

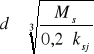
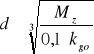
X [m]	Mz [Nm]	Dr[m]
0	14,6	0,009
0,1	110	0,023
0,2	220	0,029
0,3	315	0,033
0,4	384	0,035
0,5	442	0,037
0,6	580	0,040
0,7	725	0,043
0,8	600	0,041
0,9	320	0,033
1	14,6	0,009

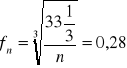
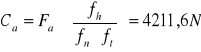
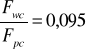
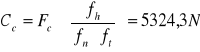
Dobór wpustów PN-70/M-85005

W miejscu koła zębatego o zębach skośnych wybieram wpust 10x8
l=21,1

W miejscu koła zębatego o zębach prostych wybieram wpust 14x9
l=32,6

W miejscu koła pasowego wybieram wpust 12x8
l=24,1

dla skręcania

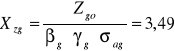
dla skręcania

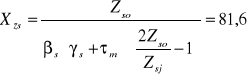
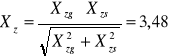
Dane | Obliczenia i szkice | Wyniki 1

Temat: Zaprojektować wał maszynowy zgodnie z rysunkiem: N=21 [kW]

n=1500 [obr/min]

l=1 m.

Odległości pomiędzy punktami A÷E wynoszą w każdym miejscu 0.2 [m]

+30% +30%

A B C D E

Rozkład siły na wale.

40% 70% 30%

A B C D E

0,3N 0,7N 0N 0,3N

- miejsce odczytu wartości siły w obliczeniach momentu skręcającego.

W zadaniu koło zębate o zębach skośnych jest w punkcie B, koło zębate o zębach prostych jest w punkcie D, dwie podpory w punktach A (ruchoma) i C (stała), a koło pasowe w punkcie E. Dobieram materiał na wał i określam podstawowe parametry wytrzymałościowe na postawie norm. Na wykonanie wału wybieram stal węglową St5 której parametry wytrzymałościowe są następujące:

kgo=120 Mpa, ksj =130 Mpa

Dane Obliczenia i szkice Wyniki 2

Wartość sił dla koła zębatego o zębach skośnych:

Obliczamy wartość momentu skręcającego dla koła zębatego:

N=21 [kW]

n=1500

[obr/min]

MS=133,7 [Nm]

αo=20°

przyjmujemy moduł m=0,005 [m]

Teoretyczna graniczna liczba zębów zg dla kąta przyporu αo=20° wynosi:

Przyjmujemy liczbę zębów koła zębatego równą 20

z1=20

Obliczam wymiary charakteryzujące ząb:

- wysokość głowy zęba ha = m = 0,005 [m]

ha=0,005 [m]

- wysokość stopy zęba

h f

= ,1,25 ⋅ m = 0,0062

hf=0,0062 [m]

- wysokość całkowitą zęba

h = ,2,25 ⋅ m = 0,0112

h=0,0112[m]

zg=20

Wyznaczam średnicę podziałową ze wzoru:

m=0,005m

β=100

do=0,101[m]

Obliczam średnicę wierzchołków zębów:

da1=0,111[m]

df1=0,089[m]

Obliczam średnicę podstaw zębów:

Obliczam wartość podziałki:

p1=0,0159[m]

Ms=133,7[Nm]

Obliczenie siły obwodowej Pob1

do1=0,101[m]

P01=2409 [N]

Obliczenie siły promieniowej Pr1

β=10°

αwn=20°

Pr1=909,52[N]

Obliczenie siły osiowej

Pos1=424,77[N]

Obliczam wartość sił dla koła zębatego o zębach prostych:

N=21 [kW]

Przyjmujemy liczbę zębów równą 26, jak również pozostałe wartości kątów αwn=20°. β=10°. Wartość modułu równą 0,005m.

n=1500

[obr/min]

MS=40,11[Nm]

Dane | Obliczenia i szkice | Wyniki 3

Obliczam wymiary charakteryzujące ząb:

m=0,005

- wysokość głowy zęba ha = m = 0,005m m005

ha2=0,005m

- wysokość stopy zęba

hf2=0,0062m

- wysokość całkowitą zęba

h2=0,0112m

Wyznaczam średnicę podziałową ze wzoru:

zg=28 m=0,005m β=100

do2=0,12[m]

Obliczam średnicę wierzchołków zębów:

da1=0,13[m]

p₁=0,015[m]

Obliczam średnicę podstaw zębów:

df1=0,1[m]

wartość podziałki

Obliczenie siły obwodowej Pob2

β=10°

MS=76,4[Nm]

Pob2=668,5[N]

Obliczenie siły promieniowej Pr2

P

= P

tg (α wn ) = 252,39[N]

αwn=20°

r 2

o 2

cos(

β

)

Pr2=252,39[N]

Wyznaczenie sił w przekładni pasowej.

Dane | Obliczenia i szkice | Wyniki 4

Z tablic dobieram znormalizowaną średnicę koła pasowego d1=0,16m. Przyjmuję przełożenie przekładni u=1,6.

d1=0,16[m].

d2=0,256[m]

Obliczenie odległości między kołami przekładni pasowej.

Minimalną odległość między osiami kół obliczam z następującej zależności:

amin=0,338[m]

d1=0,16[m].

d2=0,256[m.]

Maksymalna odległość między osiami kół wynosi:

amax=0,832[m]

a=0,5 [m].

a=0,5 [m].

amin ≤ a ≤ amax zatem dla danej przekładni pasowej przyjmuję odległość między osiami kół

równą 0,5 [m]

Obliczam kąt opasania na kole czynnym.

d2=0,256[m].

d1=0,16[m].

d1=średnica czynnego koła pasowego

α = 2 arccos d1 = 161,58

α=2,82 rad

α=161,580

2a

Obliczam kąt rozwarcia cięgien

γ=0,32 rad

γ=20,370

γ = π − α = 20,37

Obliczam siłę obwodową dla przekładni pasowej. Moc w tym miejscu jest równa 0,4 N.

N=21 [kW]

n=1500 [1/min]

MS=53,48[Nm]

d1=0,16[m].

PO=668,5[N]

Dane | Obliczenia i szkice | Wyniki 5

n=1500

[obr/min]

Obliczam napięcia cięgien ze wzoru Eulera

V = π d1n = 12,56

d1=0,16[m]

Obliczam prędkość pasa

60

V=12,56[m/s]

Obliczam rzeczywisty współczynnik tarcia

Obliczam pozorny współczynnik tarcia, gdzie β to kąt zarysu rowka na kole

Czynnym wynoszący β=36°.

µ=0,425

β=360

µ'=1,37

wyznaczam ze wzoru Eklera wartość m

α=161,580

m=47,62

PO=668,5[N]

m=47,62

Napięcia cięgien wynoszą:

S1=682,83[N]

S2=14,34[N]

Obliczamy siłę wypadkową Q napięć w cięgnach i jej składowe:

S1=682,83[N] S2=14,34[N]

Q=668,63[N]

γ=20,370

Obliczam kąt pochylenia wypadkowej Q:

m=47,62

ν = arctg(0,16)=9,1

υ=9,1°

d2=0,256[m].

Obliczam stopień wykorzystania pasa

ϕ=0,95

Obliczam wartości składowych wypadkowej Q napięć w cięgnach:

d1=0,16[m].

QY=655,25[N]

QZ=100,29[N]

Obliczam przełożenie przekładni

ir=0,625

Dobieram współczynnik: Ci=1,10

Ci=1,15

Obliczam średnicę równoważną potrzebną do określenia typu pasa i mocy przez niego

Dane | Obliczenia i szkice | Wyniki 6

przenoszonej:

de=0,176

Odczytana z tablic moc przenoszona przez jeden pas:

N1 = 5,3[kW]

γ=20,370

Długość pasa przekładni pasowej otwartej wynosi:

a=0,5 [m].

L = 2a cos

γ

2

+

π

2

(d1 + d 2 ) +

γ

2

(d 2 − d1 ) = 1,502 [m]

L=1,5[m]

Obliczam liczbę pasów potrzebnych do przenoszenia wcześniej wyliczonej mocy

Odczytane z tablic współczynniki:

j=3

Dane | Obliczenia i szkice | Wyniki 7

Szacowanie występujących reakcji, momentów gnących i momentów skręcających.

Określam reakcje występujące w układzie X-Z

d1=0,115m

QZ=203,4 N

Rcx = Pos1 = 266,8

Rcx=266,8 N

R

+ R

= −P 1 + P 2 − Q

Pr1=656,08 N Pr2=162,3 N Pos1=266,8 N

r

y

Rcz=-145,8 N

Raz=-551,4 N

minus oznacza że źle została skierowana siła R, musimy ją skierować w drugą stronę i wtedy będzie miała znak dodatni.

Dane | Obliczenia i szkice | Wyniki 8

Pob1=1512,9 N Pob2=908,4 N Qy=702,5 N

Rcy=-399,4 N

Ray=-907,6 N

minus oznacza że źle została skierowana siła Ray musimy ją skierować w drugą

stronę i wtedy będzie miała znak dodatni.

Określam momenty zginające występujące na wale

Wyznaczam momenty zginające w płaszczyźnie X-Z

przedział 0 ≤ x₁≤0,25

Raz=-551,4 N

Mg(0)=0 Nm

Mg(0,25)=

-137,9 Nm

Raz=-551,4 N

Pos1=266,8 N

Pr1=656,08 N

d=0,115 m

Mg(0,25)=

-137,9 Nm

Mg(0,5)=

-424,4 Nm

Pos1=266,8 N

Pr1=656,08 N

Mg(0,5)=

Pr2=162,3 N

d=0,115 m

-424,4 Nm

Dane | Obliczenia i szkice | Wyniki 9

Mg(0,75)=

Pos1=266,8 N Pr1=656,08 N

-762,8 Nm

Pr2=162,3 N

Mg(0,75)=

-762,8 Nm

d=0,115 m

Rcy=-399,4 N

Mg(1)=0 Nm

Wyznaczam momenty zginające w płaszczyźnie X-Y

Ray=-907,6 N

Mg(0)=0Nm

Mg(0,25)=

-226,9Nm

Ray=-907,6 N

Mg(0,25)=

Pob1=1512,9 N

-226,9 Nm

Mg(0,5)=

-76,6 Nm

Ray=-907,6 N

Pob1=1512,9 N

Mg(0,5)=

Rcy=-399,4 N

-75,6 Nm

Mg(0,75)=

-24,1 Nm

Ray=-907,6 N

Pob1=1512,9 N

Mg(0,75)=

Pob2=908,4 N Rcy=-399,4 N

-24,1 Nm

Mg(1)=0 Nm

Dane | Obliczenia i szkice | Wyniki 10

Określam moment gnący wypadkowy

Obliczam wartość momentu zastępczego gnącego według zależności:

M

g =

M

g

2 ( xy)

+

M

g

2 ( xz)

Mg1)=0 Nm

l [m] Mg(xy) Mg(xz) Mgz

0 0 0 0

0,25 -226,9 -137,9 265,52

0,5 -75,6 -424,4 431,08

0,75 -24,1 -762,8 763,18

1 0 0 0

Mg(2)=265,5 Nm Mg(3)=431,1 Nm Mg(4)=763,2 Nm Mg(5)=0 Nm

N=17 kW N=1500 obr/min

Obliczam moment skręcający występujący wzdłuż wału

N- moc przenoszona przez wał, kW

n - prędkość obrotowa, obr/min

Ms1=32,5 Nm Ms2=75,8 Nm Ms3=75,8 Nm Ms4=75,8 Nm Ms5=32,5 Nm

Ms1=32,5 Nm

Obliczam moment skręcający Ms'

Obliczanie współczynnika redukcyjnego.

go

Ms2=75,8 Nm

Ms3=75,8 Nm Ms4=75,8 Nm Ms5=32,5 Nm

Obliczanie wartości momentu zredukowanego.

'= Ms·0,45

l [m] Ms Ms'

0 32,47 14,61

0,25 75,76 34,09

0,5 75,76 34,09

0,75 75,76 34,09

1 32,47 14,61

Ms1'=14,6Nm Ms2'=34Nm Ms3'=34Nm Ms4'=34Nm Ms5'=14,6Nm

Dane | Obliczenia i szkice | Wyniki 11

Ms1'=14,6 Nm

Ms2'=34 Nm

Obliczam moment zastępczy Mz

Ms3'=34 Nm

) 2 '2

Ms4'=34 Nm Ms5'=14,6 Nm Mg1)=0 Nm Mg(2)=265,5 Nm Mg(3)=431,1 Nm

l [m] Ms' Mgz Mz

0 14,61 0 14,61

0,25 34 265,52 267,68

0,5 34 431,08 432,45

0,75 34 763,18 763,96

Mz1=14,61Nm Mz2=267,68Nm Mz3=432,45Nm M

Mg(4)=763,2 Nm

Mg(5)=0 Nm

1 14,61 0 14,61

z4=763,96Nm

Mz5=14,61Nm

Wyznaczam średnice wału w 7 przekrojach. Wartości momentu gnącego odczytuję z charakterystyki Mgz=f(l). W przypadku, gdy moment gnący wypadkowy jest równy 0 Mg(w)=0, to średnicę wyliczamy z następującego wzoru wytrzymałościowego, mamy do czynienia tylko ze skręcaniem.

W przypadku, gdy moment gnący jest wartością większą od 0 (występuj zarówno skręcanie i zginanie) to średnice wyliczamy następująco:

Średnice wynoszą:

x [m] Mz [Nm] dr [m]

0 12 0,030

0,2 220 0,035

0,4 300 0,040

0,6 562 0,045

0,7 725 0,050

0,9 310 0,045

1 580 0,040

d1=0,009m d2=0,023m d3=0,029m d4=0,033m d5=0,035m d6=0,037m d7=0,040m

Dane | Obliczenia i szkice | Wyniki 12

Wyznaczam maksymalną strzałkę ugięcia.

Obliczam moment fikcyjny, czyli ilorazy momentów gnących wypadkowych przez moment bezwładności przekroju. (Wykres piły Mf)

x

Mg

dr

M g

[m]

[Nm]

[m] I

0 0 0,03 0

0,1 110 0,035 23,33

0,2 220 0,035 46,67

0,3 315 0,035 66,82

0,4 384 0,04 47,75

0,5 442 0,04 54,96

0,6 580 0,045 45,02

0,7 725 0,05 36,93

0,8 600 0,045 46,58

0,9 320 0,045 24,84

1 12,03 0,04 1,5

Obliczam pola trójkątów i trapezów otrzymanych na wykresie piły.

a b h S

23,33 0,1 11,67

46,67 23,33 0,1 35

66,82 46,67 0,1 56,75

47,75 66,82 0,1 57,29

54,96 47,75 0,1 51,36

45,02 54,96 0,1 49,99

36,93 45,02 0,1 40,98

46,58 36,93 0,1 41,76

24,84 46,58 0,1 35,71

1,5 24,84 0,1 13,17

Obliczam środki ciężkości otrzymanych figur. Współrzędne środków ciężkości wynoszą dla trójkątów

2

zsc= 3 a,

dla trapezu

a ⋅ c2

+ b

zsc= 3

c + b

.

Dane | Obliczenia i szkice | Wyniki 13

Nr Obszaru a b h Odległość środka ciężkości

1 23,33 0,1 0,03

2 46,67 23,33 0,1 0,056

3 66,82 46,67 0,1 0,053

4 47,75 66,82 0,1 0,047

5 54,96 47,75 0,1 0,051

6 45,02 54,96 0,1 0,048

7 36,93 45,02 0,1 0,048

8 46,58 36,93 0,1 0,052

9 24,84 46,58 0,1 0,045

10 1,5 24,84 0,1 0,035

Podział belki w celu wyznaczenia reakcji fikcyjnych nastąpił w miejscach podpór. Obliczam reakcje RA i RC. Obliczeń dokonuję dla odległości do 0,5 m.

Obliczenia są wykonane metodą analityczną. Równania sił wypisuję dla lewej części układu.

∑ M ga = 0

− ,63 2 + 0 5,

− ,0 07 ⋅ S1 − 0 156,

⋅ Rc = 0

⋅ S 2 − ,0 253 ⋅ S3 − 0 347,

⋅ S 4 − ,0 451⋅ S5 + 0 5,

⋅ cR

0 5,

⋅ Rc = 62 3,

Rc = 124 6,

N

Obliczam maksymalny moment fikcyjny dla lewej części wału.

∑ M gA = 0

− ,0 07 ⋅ S1 − 0 156,

⋅ S2 − ,0 253 ⋅ S3 − 0 347,

⋅ S4 − ,0 451⋅ S5 + 0 5,

⋅ Rc

∑

M

gA

=

125 9,

⎡ N ⎤

⎢⎣ m ⎥⎦

Obliczam wartość strzałki ugięcia w tym miejscu:

125 9,

105 ⎢ N ⎥

⋅

⎡

⎤

f

M gA m ⎦⎣

m

mm

gA =

E

=

2 1,

⋅

⎡ N1011 ⎤

⎢⎣ m 2 ⎥⎦

= 0 00599,

= 5 99,

Dane | Obliczenia i szkice | Wyniki 12

Dobór łożysk

Dobór i obliczenie współczynników ft, fh, fn

Przyjmuję współczynnik temperatury ft=0,9 dla łożysk pracujących w temperaturze powyżej

100°C.

ft=0,9

Obliczam współczynnik trwałości, przyjmując liczbę godzin pracy łożyska =20000

Lh=20000

fh=3,42

Obliczam współczynnik obrotów:

n=1500obr/min

fn=0,28

Obliczam siły wzdłużne Fw i poprzeczne Fp działające na łożyska

Ray=-907,6 N

Dla podparcia w punkcie A:

( ) ( ) ( ) ( )

Raz=-551 N

Fpa

=

Ray

2 +

Raz

2

=

-907,6

2 +

−

551 6,

2

=

1061

N

Fpa=1061 N

Xa=1,

waF =0 brak siły osiowej w punkcie A

Obliczam stosunek siły wzdłużnej do poprzecznej w punkcie C

F_wa/F_pa = 0

ponieważ stosunek ten jest mniejszy od wartości e odczytanej z tabeli przyjmuję więc parametry: Xa=1, Ya=0 oraz V=1, ponieważ to wałek się obraca, zatem obciążenie zastępcze wynosi:

Fwa=0

Ya=0

V=1

Fa=1061 N

Dane | Obliczenia i szkice | Wyniki 13

Fa=1061 N

Obliczam nośność ruchową łożyska. Przyjmuję ft=0,9 dla łożysk pracujący w temp >2000C

fn=0,28

fh=3,42

ft=0,9

Ca=4211,6 N

Dla punktu A dobieram łożysko toczne stożkowe serii 303 o wymiarach:

d=30 mm, D=72 mm, B=19 mm

Łożysko dobrano zgodnie z normą 30306 PN-85/M-86220

Dla podparcia w punkcie C:

Rcy=-399,4 N Rcz=-145,8 N Rcx=266,8 N

Fpc=2823,4 N

Fwc=266,8N

Fpc=2823,4 N

Obliczam stosunek siły wzdłużnej do poprzecznej w punkcie D

Fwc=266,8N

ponieważ stosunek ten jest mniejsze od wartości e odczytanej z tabeli przyjmuję więc parametry: Xc=0,44 i V=1,2; ponieważ oprawa się obraca, zatem obciążenie zastępcze wynosi:

Fpc=2823,4 N

Fc=1490,8 N

Obliczam nośność ruchową łożyska

Fc=1490,8 N

fn=0,28

ft=0,9

Cc=5324,3N

Dla punktu C dobieram łożysko toczne stożkowe serii 322 o wymiarach:

d=40 mm, D=80 mm, B=23 mm

Łożysko dobrano zgodnie z normą 32208 PN-85/M-86220

Dane | Obliczenia i szkice | Wyniki 14

Obliczam współczynnik bezpieczeństwa zmęczeniowego e miejscu koła zębatego o zębach skośnych.

Stal St5: Rr=550Mpa, Qg=370Mpa, Qs=180Mpa, Zgo=240Mpa, Zso=130Mpa, Zgj=420Mpa, Zsj=280Mpa

Amplituda naprężeń wynosi:

Mgz=265,5 Nm

d=35 [mm]

σg=63,1 MPa

Ms=34 Nm

τs=2,41MPa

ρk=3mm

ρm.=0,65mm

ρ=ρm.+ ρk=0,65+3=3,65mm

Obliczam stosunki średnic czopów w badanym przekroju, koło zębate o zębach skośnych.

D = 114,

D=40

D = 40 =

ρ = 3,65 =

d

d=35

d

35

1,14

d

35

0,104

ρ = 0,104

ηk=0,54

Odczytanie z tablic wartości odpowiednich współczynników

-współczynnik wrażliwości materiału na działanie karbu ηk=0,54

-współczynnik stanu powierzchni dla zginania βp=1,08

-współczynnik stanu powierzchni dla skręcania βps=1,06

-współczynnik kształtu dla zginania αkg=1,6

-współczynnik kształtu dla skręcania αks=1,3

Obliczanie współczynnika karbu dla zginania

d

ηk=0,54 βp=1,08 βps=1,06 αkg=1,6 αks=1,3

βp=1,08

βps=1,06

βzg=1,32

αkg=1,6

dla skręcania

αks=1,3

βks=1,19

Dane | Obliczenia i szkice | Wyniki 15

Obliczenie współczynnika spiętrzenia naprężeń dla zginania

βp=1,08 βps=1,06 βzg=1,32 βks=1,19

βg=1,4

βs=1,25

Zgo=240Mpa, Zso=130Mpa, Zgj=420Mpa,

Odczytanie z tablic współczynnika wielkości przedmiotu dla zginania γg=1,45

dla skręcania γs=1,25

Obliczenie zmęczeniowego współczynnika bezpieczeństwa dla zginania

γs=1,25

γg=1,45

Zsj=280Mpa

βg=1,32 βs=1,19 γs=1,45 γg=1,25

Xzg=3,49

σag=64,7 MPa

τas=2,66 MPa

Xzs=81,6

Xzg=3,49

Całkowity współczynnik bezpieczeństwa wynosi

Xzs=81,6

Xz=3,48

X1=1,2

X2=1,1

Obliczenie wymaganego współczynnika bezpieczeństwa

Xzw=1,32

X3=1

X4=1

Xz=3,48

Xzw<Xz

1,32<3,48

Warunek został spełniony

---