SPRAWOZDANIE Z LABORATORIUM Z FIZYKI

ĆWICZENIE NR 2.

ANALIZA DRGAŃ MECHANICZNYCH W STRUNACH.

Grupa T - 13

SEKCJA VI

Marcin Cholewa

Stanisław Wawszczak

WSTĘP TEORETYCZNY.

Drgające ciało przekazuje część swojej energii otoczeniu. W następstwie tego cząsteczki ośrodka sąsiadujące z nim zostają wprawione w ruch. Poprzez oddziaływanie cząsteczek ośrodka ze sobą następuje propagacja fali mechanicznej. Gdy drgania cząsteczek ośrodka zachodzą w kierunku ruchu fali, to fale nazywamy podłużnymi. Gdy drgania rozchodzą się w płaszczyźnie prostopadłej do kierunku propagacji fali to fale nazywamy falami poprzecznymi. Mechaniczne fale podłużne rozchodzą się w każdym ośrodku materialnym, natomiast mechaniczne fale poprzeczne propagują się jedynie w ośrodkach o sprężystości postaci.

FALE POPRZECZNE.

Załóżmy, iż struna jest zamocowana w punktach O oraz O` i wykonuje drgania w płaszczyźnie XY. Falę o tak uporządkowanych drganiach nazywamy falą spolaryzowaną liniowo. Na element struny rozciągający się od punktu X₁ do X₂ z każdej strony działa jednakowa siła napinająca N. rozpatrzmy ruch pewnego elementu struny wytrąconego z położenia równowagi w kierunku osi Y. Składowa wypadkowej siły działającej na element struny w tym kierunku wynosi:

gdzie Θ₁ oraz Θ₂ oznaczają kąty nachylenia elementu struny względem osi X w punktach o współrzędnych x₁ oraz x₂.

FALE STOJĄCE.

Ponieważ rozpatrywana struna jest zamocowana na końcach, to fala propagująca w kierunku jej końca odbija się od przeszkody i propaguje w kierunku przeciwnym. Gdy długość L struny spełnia warunek:

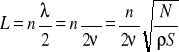
to w wyniku nałożenia fal biegnących w przeciwnych kierunkach powstaje tzw. fala stojąca określona równaniem: y=A_ycos(ωt+σ).

Powyższe równanie jest słuszne przy założeniu, iż amplituda fali nie zmienia się przy odbiciu.

Należy zwrócić uwagę, że w przypadku, gdy odbicie następuje od ośrodka znacznie gęstszego i o bardzo dużej masie, niemożliwe jest pobudzenie do drgań cząsteczek tego ośrodka przez falę nań padającą. W przypadku odbicia fali od ośrodka rzadszego na końcu struny musi wystąpić tzw. strzałka fali, czyli miejsce w którym drgania struny mają największą amplitudę.

PRZEBIEG ĆWICZENIA.

Analiza drgań metalowej struny poziomej.

1. Zmierzyliśmy 5-krotnie długość struny L oraz jej średnicę 2r.

2. Ustawiliśmy elektromagnes w połowie długości struny i włączyliśmy prąd w obwodzie elektromagnesu pobudzając do drgań strunę. Przesuwając szalkę z odważnikami o masie m na ramieniu dźwigni napinającej strunę tak dobraliśmy siłę napinającą, aby uzyskać wzbudzenie pierwszej harmonicznej (n=1) fali stojącej w strunie. Zanotowaliśmy masę odważników oraz położenie szalki na dźwigni.

3. Zmierzyliśmy rozkład amplitudy drgań struny wzdłuż fali stojącej.

4. Analogicznie do p.2 i3 pomiary przeprowadziliśmy przy wzbudzeniu drugiej (n=2) i trzeciej (n=3) harmonicznej fali stojącej. Za każdym razem elektromagnes ustawialiśmy na 1/2n długości struny.

OPRACOWANIE WYNIKÓW.

1. Przebieg zależności amplitudy drgań od położenia wzdłuż struny poziomej dla wszystkich badanych drgań harmonicznych. (WYKRES I)

2. Wartości średnie oraz odpowiadające im odchylenie standardowe długości i średnicy strun.

- wartości średnie długości i średnicy struny;

- odchylenia standardowe

	Długość L [mm]	Średnica 2r [mm]
1	1080	0,30
2	1082	0,29
3	1078	0,30
4	1081	0,28
5	1083	0,31
x	1080,80	0,296
	0,86	0,005

[mm]

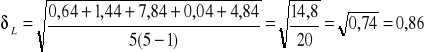
[mm]

[mm]

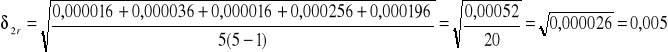
[mm]

[m]

[m]

3. Wartości sił napinających.

gdzie R - promień bloczka (R=3 cm), do którego przymocowana jest struna, w - odległość szalki od początku dźwigni, g - przyspieszenie grawitacyjne, m - masa odważników.

n=1 ;
[N]

n=2 ;
[N]

n=3 ;
[N]

4. Obliczenia niepewności wyznaczonych wartości T.

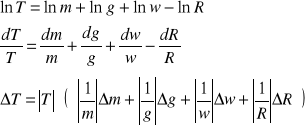
dla T₁:

[N]

dla T₂:

[N]

dla T₃:
[N]

T₁=19,21±1,49 [N]

T₂=3,45±0,31 [N]

T₃=0,00±0,00 [N]

5. Wykres ilustrujący zależność liczby obserwowanych połówek długości fali od odwrotności pierwiastka siły napinającej - WYKRES II.

6. Wyznaczanie parametrów kierunkowych prostej aproksymującej:

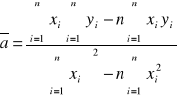
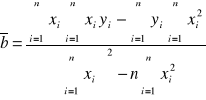
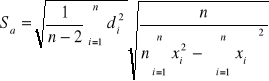
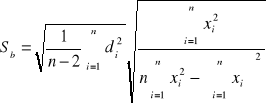
[N^1/2]

[1]

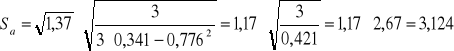
[N^1/2]

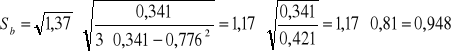
[1]

[1]

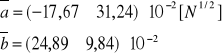
7. Wyznaczanie gęstości masy ρ struny.

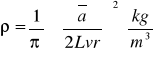
gdzie: r - promień struny,

L - długość struny,

v - częstotliwość wymuszonych drgań (v=50Hz),

a - parametr kierunkowy wyznaczony w p.6

2r=0,00029 [m]; L=1,080 [m]; v=50 [Hz]; a=-17,67 [N^1/2].

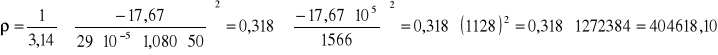
8. Wyznaczanie niepewności wyznaczonej wartości ρ.

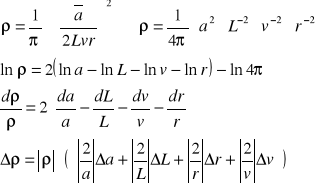
9. Wyznaczanie prędkości propagacji fal w strunie.

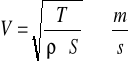
gdzie: T - wartość siły napinającej;

ρ - gęstość struny;

S - pole przekroju.

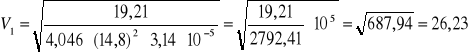
[m/s]

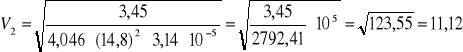
[m/s]

10. Obliczanie niepewności wartości V.

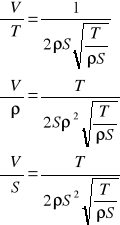
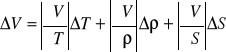
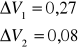
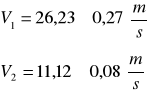
ZESTAWIENIE WYNIKÓW.

[m]

[m]

T₁=19,21±1,49 [N]

T₂=3,45±0,31 [N]

T₃=0,00±0,00 [N]

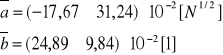
WNIOSKI.

W powyższym ćwiczeniu analizowaliśmy drgania mechaniczne w metalowej strunie poziomej.

Uzyskaliśmy wzbudzenie pierwszej, drugiej i trzeciej harmonicznej fali stojącej.

Z analizy wykresu zależności amplitudy drgań od położenia wzdłuż struny stwierdziliśmy, że są one bardzo podobne do sinusoidy, co świadczy o dobrze wykonanym ćwiczeniu.

Z analizy wykresu zależności liczby obserwowanych połówek fali od odwrotności pierwiastka siły napinającej strunę, stwierdzamy iż jest to zależność liniowa, bardzo zbliżona do prostej.

---