Podstawy elektroniki i techniki cyfrowej.
Ćwiczenie nr 9: Podstawy syntezy kombinacyjnych układów logicznych.
Kodery i dekodery.
Projekt alarmu.
Należy zaprojektować obwód spełniający funkcję: zadanie włączenia alarmu, kiedy otwarte są którekolwiek z drzwi, a kierowca siedzi na swoim miejscu. Wejścia oznaczamy: L - lewe drzwi, P - prawe drzwi, S - kierowca, a wyjście jako Y. Alarm pobudzany jest stanem wysokim na tym wyjściu.
a) przyjmujemy, że czujniki generują stan logiczny 1 (H) gdy drzwi są otwarte /
kierowca siedzi
Alarm ma być włączany w przypadku, gdy kierowca siedzi na miejscu, a którekolwiek z drzwi zostały otwarte. Na podstawie tych informacji tworzymy tabelę:
L |
P |
S |
Alarm |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
A = (~L ∧ P ∧ S) ∨ (L ∧ ~P ∧ S) ∨ (L ∧ P ∧ S)
Aby zminimalizować otrzymaną funkcję A użyjemy tablicy Karnaugha:
S \ LP |
00 |
01 |
11 |
10 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
1 |
Otrzymujemy znacznie prostszą postać funkcji:
A = (P ∧ S) ∨ (L ∧ S)
Stąd: A = S ∧ (P ∨ L)
Do zbudowania układu potrzebne będą więc tylko 2 bramki: AND i OR.
Gotowy układ wygląda następująco i działa zgodnie z założeniami:
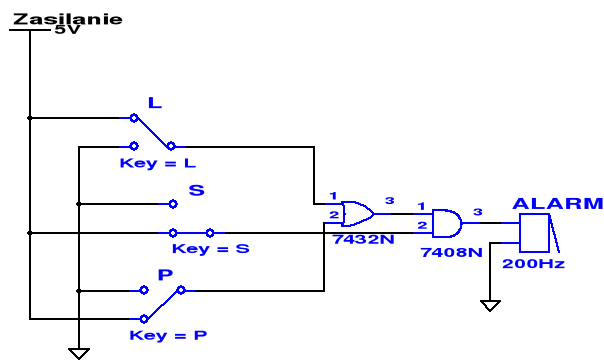
b) przyjmujemy, że czujniki generują stan logiczny 0 (L) gdy drzwi są otwarte /
kierowca siedzi
Ponownie dane o układzie gromadzimy w tablicy Karnaugha:
|
|
01 |
11 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
Funkcja wynikowa wygląda następująco: A = (~S ∧ ~L) ∨ (~P ∧ ~S)
A = ~S ∧ (~L ∧ ~P) A = ~S ∧ ~(L ∧ P)
Stąd: A = ~(S ∨ (L ∧ P))
Do budowy układu użyliśmy 2 bramek: AND i NOR:
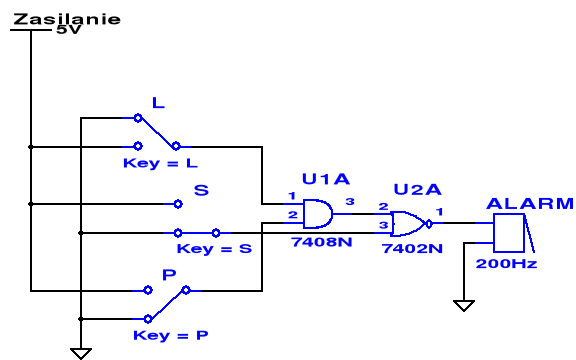
Transkoder kodu BCD na kod wskaźnika 7-segmentowego.
Naszym zadaniem jest zbudowanie układu sterującego 7-segmentowym wyświetlaczem.
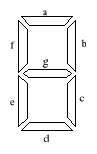
Wyświetlacz ma 7 wejść - każde odpowiada ze zapalenie kolejnego segmentu (a-g). Dany segment jest załączony, gdy na jego wejście
podany jest stan logiczny 0 (L).
Dla uproszczenia bieremy pod uwagę tylko liczby od 0 do 7.
Wtedy do reprezentacji binarnej każdej z liczb wystarczą tylko 3 bity.
W poniższej tabeli umieszczone są dane o stanie wszystkich segmentów w zależności
od syganłów podanych na wejścia A, B, C.
liczba |
segmenty wyświetlacza |
|||||||||
dec. |
kod BCD |
|
||||||||
|
A |
B |
C |
a |
b |
c |
d |
e |
f |
g |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
3 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
4 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
5 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
6 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
7 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Dla każdego segmentu wyznaczamy funkcję określającą jego stan przy użyciu tablic Karnaugha:
Segment „a”
C \ AB |
00 |
01 |
11 |
|
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
a= (~A ∧ ~B ∧ C) ∨ (A∧ ~B ∧ ~C) = ~B ∧ ((~A ∧ C) ∨ (A ∧ ~C))
Segment „b”
C \ AB |
00 |
01 |
|
10 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
b= (A ∧ B ∧ ~C) ∨ (A ∧ ~B ∧ C) = A ∧ ((B ∧ ~C) ∨ (~B ∧ C))
Segment „c”
C \ AB |
00 |
|
11 |
10 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
c= ~A ∧ B ∧ ~C = ~(A ∨ C) ∧ B
Segment „d”
C \ AB |
00 |
01 |
11 |
|
0 |
|
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
d= (~A ∧ ~B ∧ C) ∨ (A ∧ B ∧ C) ∨ (A ∧ ~B ∧ ~C) =
C ∧ (~(A ∨ B) ∨ (A ∧ B)) ∨ (A ∧ ~(B ∨ C))
Segment „e”
C \ AB |
00 |
01 |
11 |
|
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
e= C ∨ (A ∧ ~B)
Segment „f”
C \ AB |
00 |
01 |
11 |
10 |
0 |
|
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
f= (~A ∧ C) ∨ (~A ∧ B) ∨ (B ∧ C) = (~A ∧ (C ∨ B)) ∨ (B ∧ C)
Segment „g”
C \ AB |
|
01 |
11 |
10 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
g= (~A ∧ ~B) ∨ (A ∧ B ∧ C) = ~(A ∨ B) ∨ (A ∧ B ∧ C)
Mając te dane możemy już skonstruować układ sterujący wyświetlaczem:
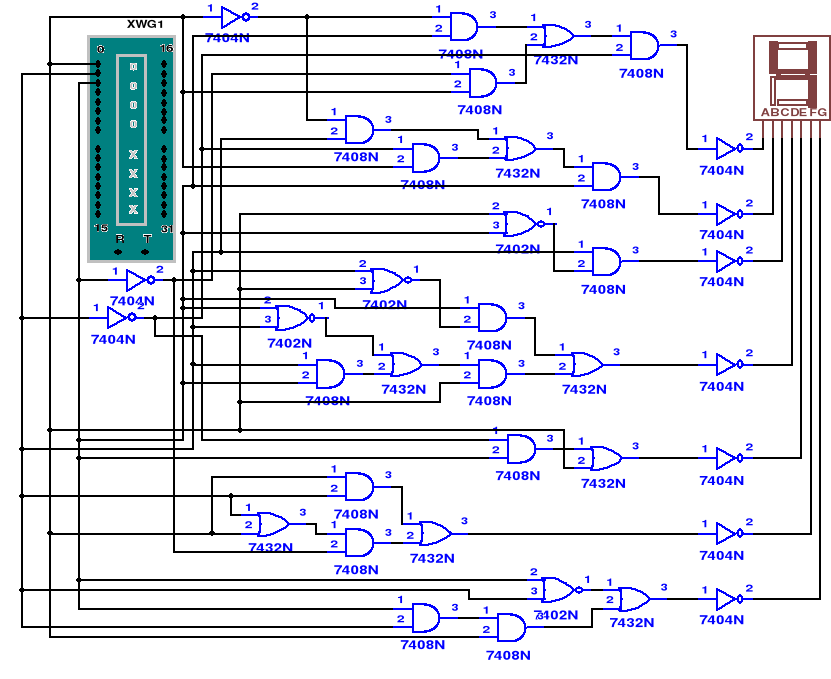
Liczby w kodzie BCD podajemy na 3 wejścia używając generatora słów. Na wyświetlaczu obserwujemy zmieniające się od 0 do 7 liczby.
strona 1/5
Wyszukiwarka