Def. Szereg liczbowy nazywamy zbieżnym, jeżeli ciąg sum częściowych jest zbieżny do granicy właściwej S.=lim Sn ( Szereg zbieżny posiada sumę, rozbieżny jej nie posiada )
Def. Równość dwóch szeregów. Uwaga!! Z równości szeregów wynika równość ich sum, ale nie na odwrót.
San=Sbn =Λan=bn
Def. Iloczynu przez liczbę. aSan=S(aan) gdzie a- stała
Def. Szereg S (an+bn) nazywamy sumą szeregów S an , S bn
Tw. Jeżeli szeregi S an; S bn są zbieżne, a ich sumy wynoszą odpow. S1 i S2 to suma S (an+ bn ) wynosi S1+S2 natomiast S a an= a S1. (Tw. To działa tylko w tą stronę)
Tw Warunek konieczny zbieżności szeregu: Jeżeli szereg San jest zbieżny, to lim an=0
Dowód:
an=Sn-Sn-1 ; lim an= lim (Sn-Sn-1) = lim Sn - lim Sn-1 = S-S=0
Szereg geometryczny:
Saqn-1 lub Saqk
1. Jeżeli a=0 to szer. zb. & S= 0
2. Jeżeli a≠0 to szer. geom.
-dla q<1 szer. geom. zb. i S=a/1-q
-dla q>1 szer. geom. rozb.
Szereg Dirchleta. S1/na , a∈R, dla α>1 sz zbieżny; dla a ≤1 sz rozbieżny.
Szereg naprzemienny Szereg Σ(-1)n+1an, gdzie an>0 dla n=1,2,3,… nazywamy szer naprzemiennym.
Tw. Jezeli ciąg sum częściowych szeregu o wyrazach nieujemnych jest ograniczony z góry, to szereg ten jest zbieżny.
Dowód:
Sn=a1+ a2+ a3+…+ an Λ an≥0, ciąg Sn jest ciągiem niemalejącym, ciąg ograniczony z góry z założenia. Każdy ciąg monotoniczny i ograniczony jest zbieżny ⇒ Sn -jest zbieżny.
Kryterium porównawcze:
Jeżeli wyrazy szeregów Σ an i Σ bn są nieujemne, a ponadto istnieje taka liczba naturalna n0 , że n> n0 i spełniona jest nierówność an≤ bn, to:
- ze zbieżności szer bn wynika zbieżność szeregu an
- z rozbieżności szeregu an wynika rozb szeregu bn
Dowód:
Sn=Σ an - chcemy pokazać, że jest zbieżny.
Sn = Sn0+Σak ≤ Sn0 +Σbk ≤ Sn0 + B;
k= n0 +1 ciąg sum częściowych Sn =Sn0 + B jest ograniczony stąd wynika zbieżność Σbk\n z założenia zbieżny i równy B.
Kryterium d'Alamberta:
Jeżeli istnieje granica właściwa lub niewłaściwa g=lim an+1/an, to szereg Σan o wyrazach dodatnich jest zbieżny, gdy g<1, natomiast rozb dla g>1.
Kryterium Cauchyego:
Jeżeli istnieje granica właściwa lub niewłaściwa g=lim n√an, to szereg o wyrazach nieujemnych jest zbieżny gdy g<1, natomiast rozb dla g>1.
Kryterium całkowe:
Niech funkcja f(x) będzie funkcją ciągłą, malejącą i dodatnią dla x≥ n0∈N wówczas war koniecznym i dostatecznym zbieżności takiego szeregu jest zbieżność całki n0∫∞ f(x)dx
Kryterium Leibniza:
Jeżeli ciąg {an} jest nierosnący oraz lim an=0, to szereg naprzemienny jest zbieżny.
[Ciąg nierosnący Λan+1≤an ]
Kryterium Weierstrassa:
Jeżeli Σan liczb. jest zbież i jeżeli![]()
spełniona jest nierówność fn(x)≤an to Σ funkcyjny jest zbieżny jednostajnie i bezwzględnie w zbiorze A. Σan nazywamy majorantą Σ funkcyjnego.
Dowód:
Σan jako zbieżny musi spełniać warunek:
![]()
![]()
![]()
![]()
- war. konieczny i dostateczny zb Σ funkcyjnego.
Def: Szereg Σan , nazywamy bezwzględnie zbieżnym
jeżeli jest zbieżny Σ złożony z bezwzględnych wartości. Jeżeli Σan jest zb. bezwzględnie, to jest zbieżny. (Σan )=Σ (an). Jeżeli Σ jest zbieżny to nazywamy go warunkowo zbieżnym.
Def. Iloczyn Caychy'ego szeregów:
Szereg Σan, gdzie an = Σ ak bn-k+1; n=1,2...- nazywamy iloczynem Cauchy'ego szeregów Σan i Σbn tzn:
(Σan ) (Σbn ) = Σan
(Σan ) (Σbn ) = Σan ak =Σak bn - k
Twierdzenie: Jeżeli szeregi Σan i Σbn s --> [Author:AS] ą zbieżne i chociaż jeden z nich jest bezwzględnie zbieżny, to ich iloczyn jest zbieżny.
Def. Ciąg funkcyjny:
Ciąg funkcyjny w zbiorze A jest to przyporządkowanie każdej liczbie naturalnej dokł. jednej określonej na tym zbiorze. Funkcję przyporządkowaną liczbie naturalnej n ozn. fn(x) natomiast cały ciąg będziemy oznaczać {fn (x) } który po napisaniu daje: (f1 (x) i f2 (x), ...). Jeżeli ciąg funkcyjny {fn(x)}jest określony w A, to dla każdego x0∈A do funkcji granicznej z ciągu funkcyjnego, otrzymamy konkretny ciąg liczbowy {fn(x0)}, który jest zbieżny lub rozbieżny.
Def. Zbieżność ciągu funkcyjnego do funkcji granicznej:
Ciąg funkcyjny {fn(x)} jest zbieżny w A do funkcji granicznej f(x), co zapisujemy limn→∞fn(x)-f(x) lub fn(x) ne→∞→ f(x) ⇔ Λε>0 Λx∈Α Vs Λn>s. fn(x)- f(x)<ε oprócz zbieżności ciągu funkc. mówimy o jego zbieżności jednostronnej, którą ozn. symbolem: Λfn(x) A⇒f(x) ⇔ Λε>0 Vδ Λx∈A fn(x)- f(x)<ε
Dla zb. zwykłej liczba δ ma istnieć dla każdego ε>0 i x∈A
Dla zb. jednostronnej ma mieć jednakową wartość dla całego zbioru A
Ze zbieżności jednostronnej wynika zbieżność zwykła
[fn(x) A⇒ f(x)] ⇒ [fn(x) e→ f(x)]
Tw. Granica jednostajnie zb. ciągu f. ciągłych jest f. ciągłą
Warunek Cauche'go:
Na to aby ciąg fn(x) był zbieżny jednostajnie w zbiorze A potrzeba i wystarcza aby Λε>0 Vr że Λn>r zachodzi [fn(x) - fr(x)]<ε
Tw. Całkowanie szeregu funkcyjnego:
Jeżeli Σfn(x) o wyrazach ciągłych w przedziale <a,b> jest w tym przedziale jednostajnie zbieżny to 0∫b[Σfn(x)]dx=Σ0∫bfn(x)dx.
Tw. Różniczkowanie szeregu funkcyjnego:
Jeżeli wyrazy sz. Funkcyjnego mają ciągłe pochodne f'n(x) w przedziale <a,b>, Σ funkcyjny Σfn(x) jest zbieżny w przedziale <a,b> a ponadto sz.Σf'n(x) jest jednostajnie zbieżny w przedziale <a,b> to:
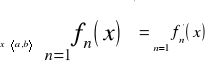
Def. Promień szeregu potęgowego:
Promieniem R zbieżności Σ potęgowego Σanxn nazywamy kres górny zbioru bezwzględnych wartości x dla Σ ten jest Σ zbieżnym.
Tw. Promień szeregu potęgowego:
Jeżeli istnieje granica:
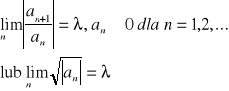
to promień zbieżności szeregu Σanxn wynosi:
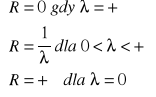
Tw. Całkowanie szeregu potęgowego:
Jeżeli x należy do wnętrza przedziału Σ pot. Σ anxn tzn. x∈(-R,R) to całka: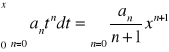
przy czym pr. zb. tego szer. jest taki jak szer. wyjściowego.
Dowód: Założenia o całkowaniu szeregu są spełnione dla:
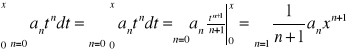
Tw. Różniczkowanie szeregu potęgowego:
Jeżeli x należy do wnętrza przedziału zb. Σ pot. Σ anxn to pochodna: ![]()
- promień zb. tego Σ jest taki sam jak Σ wyjściowego.
Uzasadnienie: zał. Tw. o różniczkowaniu Σ funkcyjnego są spełnione czyli możemy różniczkować wyraz po wyrazie:
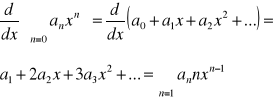
Szereg Taylora:
Niech f będzie funkcją, która ma w pewnym otoczeniu Q punktu x0 wszystkie pochodne, tzn. jest klasy C∞. Funkcję taką dla każdego x∈Q-{x0} i każdego n∈N możemy rozwinąć w Σ Taylora:
![]()
Tw. o reszcie Taylora:
Jeżeli istnieje liczba M.>0, że![]()
Spełniona jest nierówność:
![]()
czyli funkcja daje się rozwinąć w otoczeniu Q w Σ Taylora.
Dowód:
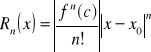
szacujemy moduł z reszty.
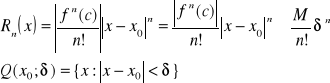
badamy zbieżność Σ z d'Alamberta:
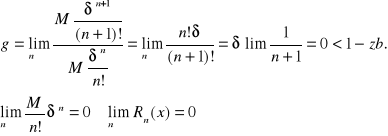
Szereg Fouriera:
Weźmy rodzinę funkcji:
![]()
Szereg funkcyjny postaci:
![]()
, gdzie an i bn są dowolnymi stałymi nazywamy szeregiem trygonometrycznym. Szereg ten ma okres T=2l.
Warunki Dirchleta:
Mówimy że funkcja f:<a,a+2l)→R ograniczona spełnia w przedziale <a;a+2l>Warunki Dirchleta jeżeli a) funkcja ta jest przedziałem monotoniczna: b) funkcja fest cuągła za wyjątkiem co najwyżej skończonej liczby punktów w których ma nieciągłość pierwszego rodzaju
Nieciągłość usuwalna Nieciągłość nieusuwalna
Lim f(x)= lim f(x)≠f(x0) Lim f(x)= lim f(x)
Χ→X0- Χ→X0+ Χ→X0- Χ→X0+
Twierdzenie: Trygonometryczny szereg Fouriera dla funkcji f. która działa w przedziale f;<a;a+2l>→R spełniająca warunki Dirchleta, jest zbieżny w każdym punkcie przedziału <a; a+2l> przy czym w dowolnym punkcie x0∈(a;a+2l) w którym f. f: fest ciągła suma szeregu wynosi f(x) natomiast w punktach x0∈(a;a+2l) w któryvh funkcja f jest nieciągła suma szeregu wynosi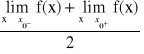
-śr. arytmet. granic jednostronnych
Na krańcach przedziału suma szer. wynosi 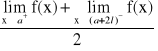
Wyszukiwarka