Wstęp teoretyczny
Szybkość reakcji jest funkcją stężenia poszczególnych reagentów A, B, C ... i jeżeli reakcja jest jednokierunkowa
(1) v = k [A]a [B]b [C]c ...
to współczynniki potęgowe a, b, c, są charakterystyczne dla reakcji i określają rząd reakcji względem danych reagentów. Suma współczynników potęgowych określa sumaryczny rząd reakcji. Poznanie rzędu reakcji ma istotne znaczenie w badaniach mechanizmów przemian chemicznych, toteż ich wyznaczenie w kinetyce chemicznej należy do podstawowych zadań.
Rzędu reakcji nie można mylić ze współczynnikami stechiometrycznymi reakcji i tzw. cząsteczkowością reakcji. Cząsteczkowość określa liczbę cząsteczek uczestniczących w elementarnej przemianie chemicznej, natomiast reakcja chemiczna zapisana w sposób sumaryczny za pomocą równania stechimetrycznego może przebiegać poprzez szereg przemian elementarnych, niekiedy w bardzo skomplikowany sposób. O kinetyce procesu decydują najpowolniejsze etapy, ale niekoniecznie tylko jeden z nich, dlatego też równanie kinetyczne (1) może przyjmować bardzo złożoną postać ze współczynnikami potęgowymi różniącymi się zasadniczo od współczynników stechiometrycznych. Tylko w przypadku prostych przemian, przebiegających jednoetapowo, sumaryczny rząd reakcji, cząsteczkowość i suma współczynników stechiometrycznych pokrywają się. Ponieważ liczba cząsteczek biorących udział w elementarnej przemianie jest z reguły mała (są to najczęściej dwie cząsteczki, rzadziej jedna i bardzo rzadko trzy), toteż i rzędy reakcji osiągają małe wartości. Analizę ograniczamy zwykle do reakcji o rzędowości mniejszej od 3. Warto podkreślić, że rząd reakcji może być ułamkowy, a także zerowy, co oczywiście nie oznacza, że w przemianie biorą udział ułamki cząsteczek, lub że reakcja przebiega w ogóle bez udziału substratu. Rząd reakcji można między innymi wyznaczyć metodą całkową. Metoda ta polega na pomiarze czasu, w ciągu którego przereagowuje określony ułamek substratu. Oznaczmy przez r ułamek nieprzereagowanego substratu:
.
Podstawiając wartości a1 - x i a2 - x do równania:
przekształceniu i uproszczeniu dochodzimy do wzoru:
Obliczanie wyników
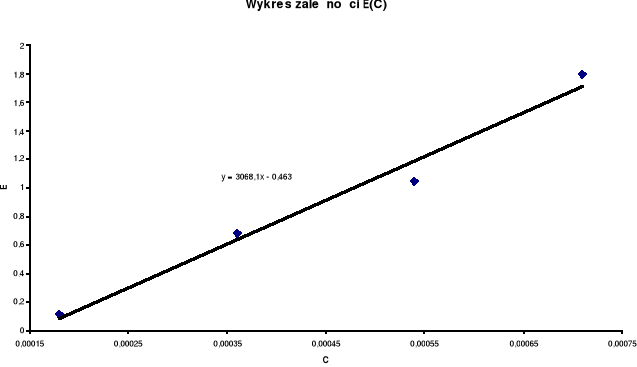
Stężenie jonów Fe3+ znaleziono z krzywej wzorcowej cechowania. W tabelach stężenie tych jonów oznaczono przez x. Stężenie substratu oznaczono przez c. Natomiast przez x' oznaczono liczby postępu reakcji.
Ilość cm3 r-ru wzorcowego Fe3+ 0,001 [mol/dm3 ] |
Stężenie jonów Fe3+ w r-rze do cechowania [mol/dm3 ] |
Ekstynk-cja |
Wartości E z linii regresji |
0,5 |
0,00018 |
0,11 |
0,17 |
1 |
0,00036 |
0,68 |
0,54 |
1,5 |
0,00054 |
1,05 |
1,28 |
2 |
0,00071 |
1,80 |
1,66 |
Wyniki pomiaru szybkości utleniania jonów Fe2+ przy stężeniu początkowym
c0 = 0.004 mol/dm3
t [s] |
180 |
480 |
780 |
1080 |
1380 |
1680 |
E |
0,21 |
0,405 |
0,575 |
0,74 |
0,87 |
1,20 |
x * 10-5 |
21,94 |
28,29 |
33,83 |
39,21 |
43,45 |
54,20 |
c * 104 |
37,69 |
37,47 |
35,38 |
34,39 |
33,62 |
31,66 |
1/c * 10-4 |
0,0265 |
0,0267 |
0,0283 |
0,0291 |
0,0297 |
0,0316 |
x' |
0,0549 |
0,0707 |
0,0846 |
0,0980 |
0,1086 |
0,1355 |
Wyniki pomiaru szybkości utlenienia jonów Fe2+ przy stężeniu początkowym
c0 = 0.0025 mol/dm3
t [s] |
180 |
480 |
780 |
1080 |
1380 |
1680 |
E |
0,08 |
0,12 |
0,175 |
0,225 |
0,27 |
0,315 |
x * 10-5 |
17,70 |
19,00 |
20,79 |
22,42 |
23,89 |
25,36 |
c * 104 |
23,26 |
23,02 |
22,80 |
22,47 |
22,25 |
21,92 |
1/c * 10-4 |
0,0430 |
0,0434 |
0,0439 |
0,0445 |
0,0449 |
0,0456 |
x' |
0,0708 |
0,0760 |
0,0832 |
0,0897 |
0,0956 |
0,1014 |
Na wykresie zależności 1/c od t spełniona jest bardzo dobrze liniowa zależność dla obu stężeń początkowych, przy czym proste są do siebie równoległe.
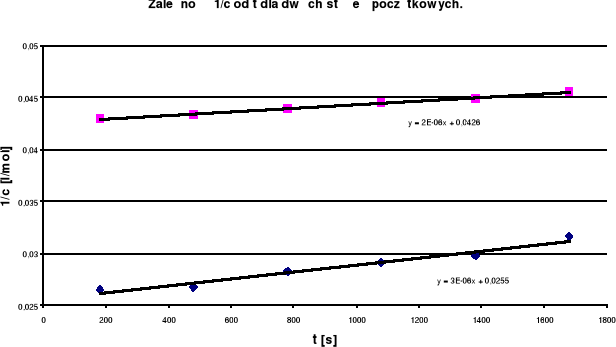
Z równań prostych wyznaczam k :
reakcja 2 rzędowa ![]()
z tego y = b + a x
- dla prostej y = 1,7E-0,6 x - 0,0426 k = 0,017![]()
- dla prostej y = 3,4E-06 x -0,0255 k = 0,034![]()
Do wyznaczenia rzędu reakcji zastosujemy metodę całkową. W tym celu sporządzamy wykresy zależności liczby postępu reakcji od czasu.
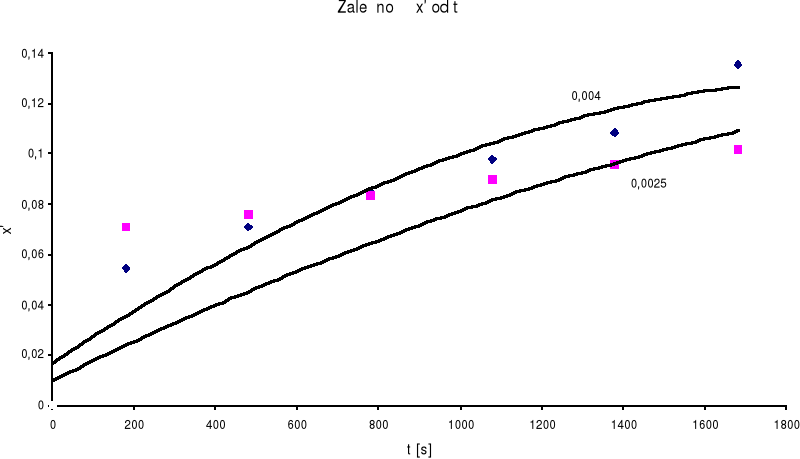
Z wykresu odczytujemy wartości t1 i t2 dla dowolnej wartości liczby postępu reakcji i wstawiamy do równania :
I tak dla x' = 0.0980 t1 = 1080 , a t2 =
a - stężenia początkowe
Stąd n =
Omówienie wyników :
Szybkość rozpatrywanej reakcji jest wprawdzie zależna również od stężenia jonów wodorowych, jednak w warunkach doświadczenia stężenie to można przyjąć jako stałe (duży nadmiar w stosunku do reagujących jonów Fe3+ i ClO3- ).
Zarówno metoda graficzna jak i całkowa potwierdzają, że jest to reakcja II rzędu. Wartość liczbowa n wynikająca z obliczeń jest wprawdzie nieco ............ od 2, jest to typowe dla tej metody; daje ona oszacowanie rzędu reakcji.
27.11.2000
Kordus Krzysztof
Wyznaczanie rzędu reakcji metodą całkową.
Wyniki:
Krzywa cechowania :
λmax. = 500nm
cm3 Fe3+ |
E |
0,5 |
0,11 |
1 |
0,68 |
1,5 |
1,05 |
2 |
1,80 |
Seria 1
t[s] |
E |
180 |
0,21 |
480 |
0,405 |
780 |
0,575 |
1080 |
0,74 |
1380 |
0,87 |
1680 |
1,2 |
Seria 2
t[s] |
E |
180 |
0,08 |
480 |
0,12 |
780 |
0,175 |
1080 |
0,225 |
1380 |
0,27 |
1680 |
0,315 |
Wyszukiwarka