LABORATORIUM FIZYKI I |
Ćwiczenie nr: 25 |
|||
|
Data: 17.10.08 |
|||
Wydział: SiMR |
Grupa: 2.3 |
Zespół: 4 |
Punktacja: |
Przygotowanie:
|
Nazwisko i Imię: Demidowski Tomasz |
|
|
||
Temat ćwiczenia: Zjawisko interferencji światła. Pierścienie Newtona, interferometr Michelsona.
|
|
Sprawozdanie:
|
||
Prowadzący:
|
|
Suma punktów:
|
||
4. Opracowanie wyników:
a) Pierwsza tabela przedstawia wyniki pomiarów średnic pierścieni Newtona oraz odpowiadający im rząd interferencji m powstałych w wyniku przepuszczenia światła monochromatycznego o długości fali l=589,3nm przez soczewkę płasko-wypukła umieszczona na płytce szklanej.
Światło o znanej długości fali l=589,3nm |
||
m |
rm [m] |
rm2 [m2] |
0 |
0,0006 |
0,00000036 |
1 |
0,001195 |
1,42803E-06 |
2 |
0,001635 |
2,67323E-06 |
3 |
0,00195 |
3,8025E-06 |
4 |
0,00225 |
5,0625E-06 |
5 |
0,0025 |
0,00000625 |
6 |
0,00281 |
7,8961E-06 |
7 |
0,00294 |
8,6436E-06 |
8 |
0,00303 |
9,1809E-06 |
9 |
0,003415 |
1,16622E-05 |
10 |
0,0037 |
0,00001369 |
11 |
0,003735 |
1,39502E-05 |
12 |
0,00389 |
1,51321E-05 |
13 |
0,003965 |
1,57212E-05 |
14 |
0,00418 |
1,74724E-05 |
Związek między promieniem Newtona RM rzędu m, promieniem krzywizny soczewki R długością fali i rzędem interferencji przedstawia wzór:
![]()
Na podstawie wyników pomiarów stworzyliśmy wykres rm2=f(![]()
).
Następnie korzystamy z metody sumy najmniejszych kwadratów podstawiając:
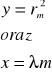
Na podstawie tych zależności program ORIGIN tworzy prostą y=Bx+A, która w najlepszy sposób pokrywa się z otrzymanymi punktami. Znając współczynniki A i B można wyznaczyć promień krzywizny soczewki:
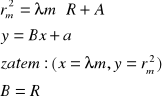
W naszym przypadku:
B=R=2,09948 [m]
b) Druga tabela przedstawia wyniki pomiarów średnic pierścieni Newtona powstałych w wyniku przepuszczenia światła białego przez filtr interferencyjny, w wyniku, czego uzyskuje się światło o nieznanej długości.
Światło o nieznanej długości fali |
||
m |
rm [mm] |
rm2 [mm2] |
0 |
0,000475 |
2,25625E-07 |
1 |
0,000325 |
1,05625E-07 |
2 |
0,000798 |
6,36006E-07 |
3 |
0,000885 |
7,83225E-07 |
4 |
0,007125 |
5,07656E-05 |
5 |
0,001253 |
1,56876E-06 |
6 |
0,001365 |
1,86323E-06 |
7 |
0,001408 |
1,98106E-06 |
8 |
0,00157 |
2,4649E-06 |
9 |
0,001658 |
2,74731E-06 |
10 |
0,001743 |
3,03631E-06 |
11 |
0,001823 |
3,32151E-06 |
12 |
0,001903 |
3,61951E-06 |
13 |
0,001985 |
3,94023E-06 |
14 |
0,002063 |
4,25391E-06 |
Na podstawie wyników pomiarów stworzyliśmy wykres rm2=f(![]()
) , gdzie R to promień krzywizny wyznaczony w poprzedniej części ćwiczenia.
Następnie korzystając z metody sumy najmniejszych kwadratów wyznaczyliśmy nieznana długość światła. W tym celu program ORIGIN wyszukuje prosta y=A+Bx, która najlepiej pokrywa się z punktami pomiarowymi. Oznaczamy
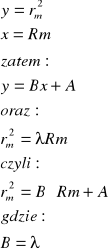
W naszym przypadku:
B=![]()
=5,83351E-7
Zatem długość nieznanej fali będzie wynosić ![]()
c) Interferometr Michelsona
Wyniki pomiarów:
d [mm] |
N |
2,5 |
0 |
2,7 |
71 |
2,9 |
136 |
3,1 |
201 |
3,3 |
263 |
3,5 |
327 |
3,7 |
390 |
3,9 |
453 |
4,1 |
517 |
4,3 |
581 |
4,5 |
645 |
Gdzie:
d - wskazanie przesunięcia zwierciadła na śrubie mikrometrycznej
n - liczba zmierzonych impulsów
W urządzeniu zastosowana dźwignie 1:10, zatem rzeczywiste przesunięcie zwierciadła będzie 10-krotnie mniejsze niż wskazanie śruby. Równocześnie przesunięcie zwierciadła o d powoduje zmianę różnicy dróg optycznych promieni interferujących o 2d.
Rzeczywiste wynik wyglądają, więc następująco
2d [m] |
N |
0,0005 |
0 |
0,00054 |
71 |
0,00058 |
136 |
0,00062 |
201 |
0,00066 |
263 |
0,0007 |
327 |
0,00074 |
390 |
0,00078 |
453 |
0,00082 |
517 |
0,00086 |
581 |
0,0009 |
645 |
Zależność na powstawanie maksimów jest następująca:
![]()
Przekształcamy powyższą zależność tak, aby mogła być wykorzystana w metodzie sumy najmniejszych kwadratów:
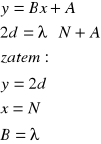
W naszym przypadku:
B=6,25012E-7=625,012E-9=625,012 [nm]
5. Rachunek błędów:
a) Podczas wykonywania pomiarów spotkaliśmy się z jednym typem błędu systematycznego, czyli błędu śruby mikrometrycznej związanego z dokładnością odczytu z podziałki:
![]()
Wartość wyliczonego promienia krzywizny soczewki także jest obarczona błędem, ponieważ wielkość ta była wyznaczana w sposób pośredni. Aby oszacować ten błąd trzeba wykorzystać metodę różniczki zupełnej.
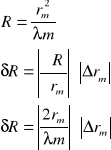
Zatem dla:
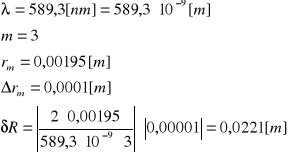
Równocześnie wartość R obarczona jest także pewnym błędem przypadkowym. Wartość tego błędu można odczytać z wykresu sporządzonego w programie ORIGIN. W naszym przypadku wynosi on
![]()
Korzystając z rozkładu T-Studenta, przyjmując:
N=15
R=2
K=15-2=13
![]()
=0,9
![]()
Zatem wartość błędu przypadkowego z uwzględnieniem rozkładu T-Studenta wynosi:
![]()
Jak widać![]()
zatem korzystam z prawa przenoszenia błędu.
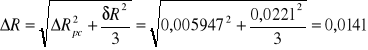
Wartość promienia krzywizny soczewki wynosi zatem:
![]()
b) W drugiej części ćwiczenia mieliśmy wyznaczyć wartość długości fali świetlnej, znając promień krzywizny soczewki oraz średnicę pierścienia Newtona.
W tych pomiarach występowa taki sam błąd systematyczny śruby mikrometrycznej:
![]()
W celu wyznaczenia długości fali użyliśmy wzoru fizycznego, zatem, czyli posłużyliśmy się metodą pośrednia, której błąd można oszacować korzystając z metody różniczki zupełnej z ta różnicą, że tym razem występują 2 zmienne, które mogą być obarczone błędem: promień krzywizny soczewki R oraz promień pierścienia Newtona ![]()
.

Zatem dla:
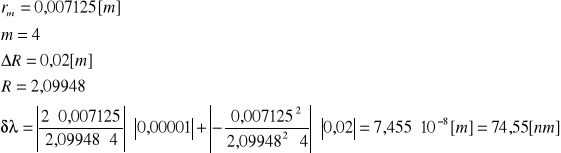
Równocześnie wartość ![]()
obarczona jest także błędem przypadkowym. Wartość tego błędu można odczytać z wykresu sporządzonego w programie ORIGIN w wyniku przeprowadzenia aproksymacji liniowej.
W naszym przypadku:
![]()
Korzystając z rozkładu T-Studenta, przyjmując:
N=15
R=2
K=15-2=13
![]()
=0,9
![]()
Zatem wartość błędu przypadkowego z uwzględnieniem rozkładu T-Studenta wynosi:
![]()
Ponieważ ![]()
zatem korzystam z metody przenoszenia błędu.
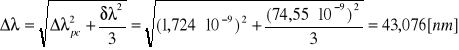
Ostateczna wartość długości nieznanej fali świetlnej wynosi:
![]()

Wyszukiwarka