Systemy ekspertowe

Temat: Wnioskowanie dedukcyjne

- naturalna dedukcja.

Prowadzący: dr Slavian Radev

Autor :Agnieszka Skarżyńska

Białystok 30-01-2004

Wnioskowanie - w węższym rozumieniu jest to dobieranie następstw dla zdań pewnych, już uznanych za prawdziwe. W szerszym rozumieniu jest to proces myślowy, w którym na podstawie zdań już uznanych (za prawdziwe) dochodzi się bądź do nowego zdania dotąd nie uznawanego, bądź do wzmocnienia pewności innego zdania w jakimś stopniu już uznanego. Wszelkie wnioskowania dzielą się na niezawodne i zawodne, czyli uprawdopodabniające. Do niezawodnych należy wnioskowanie dedukcyjne, a jego szczególną odmianą jest wnioskowanie sylogistyczne z dwóch przesłanek. Wśród różnych rodzajów wnioskowań zawodnych wyróżnia się wnioskowanie dedukcyjne, indukcyjne i przez analogię.

Wnioskowanie dedukcyjne polega na wyciąganiu wniosków z dostępnych przesłanek. Formalizacja tego sposobu rozumowania została zapoczątkowana przez Greków w trzecim wieku p.n.e. i podlegała doskonaleniu dzięki rozwojowi matematyki w ciągu ostatnich 2000 lat.

Wnioskowanie dedukcyjne jest charakterystyczne dla nauk dedukcyjnych. W tych naukach jest to jedyny uznany sposób wnioskowania. Nauki dedukcyjne to przede wszystkim teorie matematyczne. Dla nauk tych znamienne jest to, że przedstawiane są w formie systemów aksjomatycznych: z już uznanych zdań, czyli twierdzeń, wyprowadza się kolejne twierdzenia. Tak to wygląda na etapie przedstawienia systemu jako czegoś już gotowego. Proces znajdowania nowych twierdzeń i znajdowania dla nich przesłanek ma charakter twórczy i jak każdy proces twórczy nie ogranicza się do dających się opisać rodzajów rozumowań. Ważną rolę pełni w nim intuicja.

Dedukcja naturalna to bardzo intuicyjny i generujący ładne dowody system dowodzenia twierdzeń, bazowany na systemach Hilberta. Intencją jej jest jak najdalej idące przybliżenie logicznej teorii dowodu do rzeczywistej praktyki dowodowej w matematyce i innych naukach. Zauważono, że rachunki logiczne w postaci systemów aksjomatycznych z nielicznymi regułami bezpośrednio nie opisują sposobów wnioskowa­nia stosowanych w praktyce. Stąd powstał problem naturalności dedukcji. Jednym z systemów dedukcji naturalnej jest metoda dowodów założenio­wych.

(DEF. dowodu założeniowego) Dowód założeniowy jest ciągiem zdań. Te zdania to wiersze dowodowe. Zdanie, dla którego istnieje dowód to twier­dzenie. O tym, w jaki sposób buduje się dowód, mówią reguły tworzenia dowodu. Od tych reguł należy odróżnić reguły dołączania nowych wierszy dowodowych.

Wpierw omówione zostaną reguły tworzenia dowodu a następnie reguły dołączania nowych wierszy dowodowych.

REGUŁY TWORZENIA DOWODU

Podamy dwa sposoby tworzenia dowodu założeniowego, dowodu wprost i dowodu niewprost.

Przedmiot dowodu

Przedmiotem dowodu mogą być zdania. Zdanie, dla którego istnieje dowód założeniowy to twierdzenie. Dowodzić możemy również tego, że z ja­kichś danych zdań-przesłanek,

α₁, α₂, ...., α_n wynika logicznie zdanie-wniosek, α, czyli że α₁, α₂, ...., α_n |- α , co będziemy zwykle zapisywali:

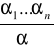
Druga możliwość jest sprowadzalna do pierwszej, a mianowicie dowód założeniowy dla

α₁, α₂, ...., α_n |- α istnieje tylko wtedy, gdy istnieje dowód założeniowy dla zdania α_{1 ^} α_{2 ^ ...^} α_n → α²³ . Pierwsza możliwość jest szczególnym wypadkiem drugiej, a mianowicie jest to sytuacja, gdy py­tamy o dowód z pustego zbioru przesłanek. Opis zasad konstrukcji dowodu można więc ograniczyć do sytuacji, gdy przedmiotem dowodu jest to, czy, α₁, α₂, ...., α_n |- α , czyli czy z α₁, α₂, ...., α_n wynika α .

Zasady dopisywania wierszy dowodowych

Dowód założeniowy jest ciągiem zdań. Poszczególne wyrazy tego ciągu, wiersze dowodowe, są dopisywane do dowodu zgodnie z określonymi za­sadami. Zasady te różnią się dla omówionych tu sposobów dowodzenia, dowodu niewprost i dowodu wprost. Wpierw podane zostaną te zasady dopisywania wierszy dowodowych, które są dla tych sposobów wspólne.

Niech przedmiotem dowodu będzie:

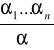
l. Jako wiersze dowodowe bierzemy wszystkie zdania α₁, α₂, ...., α_n , czyli -tak będziemy mówili - zdania znajdujące się nad kreską. Są to założenia dowodu założeniowego.

2. Jeżeli zdanie a, wyrażenie pod kreską, ma postać:

β₁ → ( β₂ → ( ... → ( β_m → β ) ... )),

to jako wiersze dowodowe możemy wziąć zdania β₁ , β₂ , ... β_m . Są to założenia dowodu założeniowego.

3. Jeżeli β jest twierdzeniem, to β może być dopisane do dowodu.

4. Niech

będzie regułą (pierwotną lub wtórną) dołączania nowych wierszy do­wodowych. Niech wpisując jednocześnie te same zdania za te same zmienne metaprzedmiotowe, występujące w Φ₁ , Φ_{2 ,} ... , Φ_m , ψ ze sche­matu Φ_i , otrzymamy zdanie β_i , l < i < m, a ze schematu ψ otrzymamy zdanie β. Jeżeli w dowodzie występują jako wiersze dowodowe zdania β₁ , β₂ , ... β_m, to jako kolejny wiersz dowodowy wolno dopisać zdanie β .

1. REGUŁY TWORZENIA DOWODU NIEWPROST

Jako założenie dowodu niewprost bierze się:

1. ^┐α

lub

2. jeśli α jest zdaniem β₁ → ( β₂ → ( ... → ( β_m → β ) ... )), to jako założenia dowodu niewprost można wziąć ^┐β.

3. Dowód kończy się, gdy dla pewnego γ otrzymuje się dwa wiersze do­wodowe, z których jeden to zdanie γ, a drugi to zdanie ^┐γ.

2. REGUŁY TWORZENIA DOWODU WPROST

2.1. Dowód kończy się, gdy jako wiersz dowodowy otrzymuje się wyrażenie znajdujące się pod kreską, czyli α

lub

2.2. jeśli α jest zdaniem β₁ → ( β₂ → ( ... → ( β_m → β ) ... )), to dowód kończy się, gdy jako wiersz dowodowy otrzymujemy zdanie β.

Zauważmy, że w każdym wypadku, gdy istnieje dowód wprost, to ist­nieje dowód niewprost. Do dowodu wprost wystarczy dopisać jako założenie

zdanie ^┐α lub ^┐β, co wolno uczynić zgodnie z zasadami tworzenia dowodu niewprost.

Obok wierszy dowodowych zaznacza się, czy zostały one przyjęte jako założenia, czy na podstawie reguł. W tym ostatnim wypadku zaznacza się użytą regułę i wiersze dowodowe, do których została zastosowana. Korzy­stać będziemy z następujących skrótów:

zał. - założenie

z.d.n. - założenie dowodu niewprost

sprzecz. - sprzeczność

Dowieść można, że wnioskowanie jest dedukcyjne wtedy i tylko wtedy, gdy ma dowód założeniowy niewprost.

Trudność praktyczną stwarzać mogą dowody w wypadku, gdy brak wierszy «nad kreską», a więc gdy mamy dowieść: ┤β a β nie jest implikacją, np. α v ^┐α . Ograniczając się do opisanych reguł tworzenia dowodu musimy przeprowadzać dowód niewprost.

REGUŁY DOŁĄCZANIA NOWYCH WIERSZY DOWODOWYCH

Reguły dołączania nowych wierszy dowodowych dzieli się na pierwotne i wtórne. Reguły pierwotne to reguły przyjęte bez dowodu. Na reguły pier­wotne nadają się reguły, które są intuicyjnie logiczne. Intuicyjność logicz­ności to kryterium o charakterze subiektywnym. Z formalnego punktu wi­dzenia chodzi zaś o takie i o tyle reguł, aby powstały system rachunku logicznego był niesprzeczny i pełny, czyli obejmował wszystkie i tylko te re­guły, które są logiczne (formalne i niezawodne): jeśli w modelu prawdziwe są przesłanki, to otrzymany zgodnie z nimi wniosek też jest w tym modelu prawdziwy. Regułami wtórnymi są wszystkie reguły udowodnione.

REGUŁY PIERWOTNE

(RO) Reguła odrywania

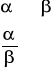
(DK) Reguła dołączania koniunkcji

(OK) Reguła opuszczania koniunkcji

(DA) Reguła dołączania alternatywy

(OA) Reguła opuszczania alternatywy

(DE) Reguła dołączania równoważności

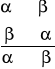
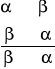
(OE) Reguła opuszczania równoważności

Bibliografia:

K Trzęsicki Elementy logiki i teorii mnogości

http://aragorn.pb.bialystok.pl/~radev/ai/se/zal/ready/jeglinski.htm

2

---