Mion (mezon μ) utworzony w górnych warstwach atmosfery przebywa do chwili rozpadu odległość 5 km z prędkością v=0.99c (gdzie c - prędkość światła).
Jak długi jest "czas życia" mionu mierzony przez nas, a jaki "czas życia" mierzony w jego własnym układzie odniesienia?
Jaką grubość atmosfery, mierzoną w jego własnym układzie odniesienia, przebędzie mion.
Dwa akceleratory dają cząstki poruszające się w przeciwne strony z prędkościami v1 = v2 = 0.9 c. Oblicz względną prędkość cząstek.
Zjonizowany atom, wyleciawszy z akceleratora z prędkością v = 0.8 c, wyemitował foton w kierunku swego ruchu. Obliczyć prędkość fotonu względem akceleratora.
Spoczywający kwadrat o boku a ustawiony jest tak, że jedna z jego przekątnych jest równoległa do osi x. Jaką figurę będzie widział obserwator jeżeli kwadrat zacznie się poruszać względem obserwatora z prędkością v równolegle do osi x? Oblicz obwód tej figury.
Udowodnić, że przy małych prędkościach (v/c << 1) relatywistyczny wzór na energię kinetyczną przechodzi w wyrażenie klasyczne.
Jakie powinno być napięcie elektryczne, aby - zgodnie z zasadami mechaniki klasycznej - poruszający się w tym polu elektron uzyskał prędkość światła? Jaką prędkość uzyska elektron w tym polu według zasad mechaniki relatywistycznej? Jak zmieni się masa elektronu? Masa spoczynkowa elektronu me=9.1*10-31kg, ładunek elektronu e=1.6*10-19C, prędkość światła c=3*108m/s. (wsk.: napięcie elektryczne U zmienia energię kinetyczną elektronu o eU.)
Oblicz energię wydzieloną w rozpadzie neutronu na proton i elektron. Masa spoczynkowa elektronu
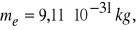
masa spoczynkowa protonu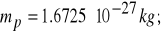
, masa spoczynkowa neutronu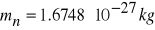
.
Wyszukiwarka
Podobne podstrony:
Elektronika 03, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
Elektronika 10, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza, Zadania z Fizyki
Elektronika 02, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
Elektronika 11, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
Elektronika 08, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza, Zadania z Fizyki
lista5MBMinna, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Elektronika 09, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
Elektronika 03, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
Fifyka komputerowa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
fiele25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
Pomia napięcia powierzchniowego, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, spr
fiele15, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
lista4elektronika(1), Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Sprawozdanie 81, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
Sprawozdanie nr12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fi
Sprawozdanie nr43 fizyka, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdan
Sprawozdanie 12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
LABORATORIUM, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Sprawozdanie 57c, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fiz
więcej podobnych podstron