Zadanie I 11

Określić promień cząsteczki tlenu O₂ przy założeniu, że ma ona ksztalt kulisty i wiedząc że wartość molowej współobjętości (objętości wyłączonej molowej) w równaniu stanu gazu rzeczywistego van der Waalsa jest równa b=32[
], zaś liczba Avogadra N_A=6,022*10²³ [
].

Dane: b=32[
], N_A=6,022*10²³ [mol^-1]; Obliczyć: r=
=?

1. Wyznaczanie objętości cząsteczki w kształcie kuli o średnicy d:

V_cz= 4/3π(
)³

2. Wyznaczanie objętości wyłączonej dla cząsteczki.
   Objętość wyłączona jest objętością w której środki cząsteczek nie mogą się poruszać ze względu na swoją wzajemną obecność i równa jest połowie objętości kuli
   o promieniu równym średnicy cząsteczki.

d V_w=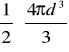
=

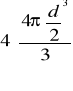
V_w=
=

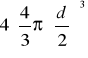
Objętość włączona zasobu ilości materii n=1[mol] cząsteczek (współobjętość molowa) równa jest iloczynowi liczby Avogadra N_A i objętości wyłączonej
cząsteczek V_w

b=N_AV_w[
]

3. Równanie stanu gazu rzeczywistego van der Waalsa odniesione do masowych gęstości zasobu określone jest związkiem:

(p+
)(ϑ-α)=RT

gdzie:

a - współczynnik kohezyjności masowej

α -współobjętość masowa (kowolumen),

Współczynnik kohezyjności masowej określony jest związkiem

a =

gdzie:

- współczynnik kohezyjności molowej

M - masa cząsteczkowa

Ciśnienie kohezyjne określone jest związkiem
, natomiast współobjętość masowa
jest równa:

α =

gdzie:

b - współobjętość molowa (objętość wyłączono molowa).

Zatem równanie van der Waalsa zapiszemy w postaci:

[p+
](ϑ-
)=RT

Relacja między masową a molową gęstością zasoby objętości określona jest związkiem

ϑ=

stąd:

(p+
)(
-
)=RT

Uwzględniając, iż:

[R] =

oraz:

MR = B

gdzie:

[B]=

po pomnożeniu przez M

Otrzymamy równanie stanu gazu rzeczywistego van der Waalsa odniesione do molowych gęstości zasobu

(p+
)( ϑ_n -b)=BT

4. Wyznaczanie promienia cząsteczki tlenu.

Dzieląc objętość wyłączoną molową cząsteczek b przez liczbę Avogarda N_A cząsteczek O₂ tlenu zawartych w 1 molu tego gazu

V_w= b/N_A

Otrzymamy objętość wyłączoną cząsteczki telu O₂ określoną związkiem:

V_w= 4[
π(
)³]

Porónując prawe strony powyższych dwóch zależności

b/N_A=
π(
)³

otrzymay promień cząsteczki telnu O₂, przy zależności, że ma ona kształt kulisty

r=
=

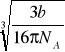
5. Rachunek mian:

[r] =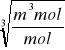
= m

6. Obliczenie wartości promienia cząsteczki tlenu.

r =
=
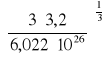
= 2,51445*10^-9 [m]

d= 5,0289*10^-9 [m] ≈ 5,03 [nm]

d

---