10. Metody optymalizacji globalnej

Optymalizacja funkcji jednej zmiennej

Dana jest funkcja:

x_m- minimum lokalne x^M-maksimum globalne

x_M- minimum globalne x_p-punkt przegięcia

Są to punkty ekstremalne funkcji f(x), które spełniają warunek konieczny istnienia minimum (maksimum) :

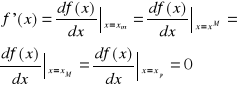
Punkt x_M będzie punktem minimum globalnego f(x) w [a, b], jeżeli:

Punkt x^M będzie punktem maksimum globalnego f(x) w [a, b] jeżeli:

Niech
. Warunkiem koniecznym istnienia punktów ekstremalnych x^* jest zależność :

Optymalizacja funkcji wielu zmiennych bez ograniczeń

Dana jest funkcja n- wymiarowa f(x),
. Zadanie optymalizacji:

Punkt x_M będzie punktem minimum globalnego f(x) w
,jeżeli:

Punkt x^M będzie punktem maksimum globalnego f(x) w
, jeżeli:

Warunkiem koniecznym istnienia punktów ekstremalnych
w zadaniu wielowymiarowej optymalizacji bez ograniczeń jest:

albo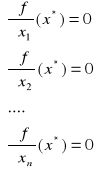

x_m

x_M

x^p

x^M

b

a

x

f(x)