Laboratorium :Algorytmy i struktury danych. |
|||
Temat: |
Rachunek macierzowy. |
||
Wykonał: |
Mariusz Daszkiewicz
|
Data:99-12-19 Gr.27 |
Ocena: |
1. Cel ćwiczenia:
Ćwiczenie ma na celu zapoznanie z komputerowa implementacją rachunku macierzowego.
Szczególną uwagę zwracać będziemy na implementację wyznaczania wyznacznika macierzy oraz macierzy odwrotnej.
2.1: Macierzą prostokątną - macierzą o wymiarach M x N nazywamy odwzorowanie
M x N R, gdzie R zbiór liczb rzeczywistych:
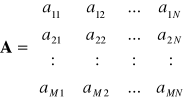
2.2: Wyznacznikiem macierzy kwadratowej A nazywamy pewną liczbę rzeczywistą przypisaną do niej detA.
![]()
gdzie:
- P(l1; l2; : : : ; ln) jest permutacją liczb l1; l2; : : : ; ln
- k jest liczba przestawień względem sekwencji początkowej
2.3: Macierz odwrotna:
Macierz odwrotna macierzy kwadratowej A o rozmiarach N x N jest, oznaczana przez A^1. Macierz A nazywamy odwracalną jeśli istnieje takie A^1 dla. którego:
A ^1A =I=AA^1
3.1: Zaimplementować procedury obliczające sumę, różnicę oraz iloczyn macierzy zadanych przez użytkownika(zakładamy, że wszelkie zmienne i stałe zostały wcześniej zadeklarowane):
3.1.1: Suma:
procedure suma;
begin
for i:=0 to n do
begin
for j:=0 to n do
begin
tab3[i,j]:=tab1[i,j]+tab2[i,j];
write(tab3[i,j],' ');
end;
writeln;
end;
end;
3.1.2: Różnica:
procedure roznica;
begin
for i:=0 to n do
begin
for j:=0 to n do
begin
tab3[i,j]:=tab1[i,j]-tab2[i,j];
write(tab3[i,j],' ');
end;
writeln;
end;
end;
3.1.3 : Iloczyn:
procedure iloczyn;
begin
b:=0;a:=0;s:=0;
for g:=0 to n do
begin
for i:=0 to n do
begin
k:=0;s:=0;
for j:=0 to n do
begin
k:=tab1[g,j]*tab2[j,i];
s:=s+k;
end;
tab3[a,b]:=s;
b:=b+1;
if b=(n+1) then b:=0;
end;
a:=a+1;
end;
for i:=0 to n do
begin
for j:=0 to n do
write(tab3[i,j],' ');
writeln;
end;
end;
3.2: Utworzyć schemat blokowy oraz zaimplementować procedurę wyznaczającą wyznacznik macierzy( zakładamy, że wszelkie zmienne i stałe zostały wcześniej zadeklarowane):
3.2.1: Schemat blokowy:
3.2.2: Wyznacznik macierzy:
procedure wyznacznik;
begin
s1:=1;s2:=1;c1:=0;c2:=0;
for i:=0 to n do
begin
for j:=0 to n do
begin
s1:=s1*tab1[j,((j+n-i)mod(n+1))];
s2:=s2*tab1[j,((n+1-j+i)mod(n+1))];
end;
c1:=c1+s1;
c2:=c2+s2;
s1:=1;s2:=1;
end;
w:=c1-c2;
writeln;
writeln('wyznacznik = ',w);}
end;
3.3: Utworzyć schemat blokowy i zaimplementować procedurę wyznaczającą macierz odwrotną( zakładamy, że wszystkie zmienne i stałe zostały zadeklarowane):
3.3.1: Schemat blokowy:
3.3.2: Macierz odwrotna:
procedure odwrotna;
begin
for i:=0 to n do
begin
r:=tab4[i,i];
for j:=i to n do
tab4[i,j]:=tab4[i,j]/r;
for j:=0 to n do
tab5[i,j]:=tab5[i,j]/r;
for k:=(i+1) to n do
begin
h:=tab4[k,i];
for l:=i to n do
tab4[k,l]:=tab4[k,l]+((-1)*h*(tab4[i,l]));
for l:=0 to n do
tab5[k,l]:=tab5[k,l]+((-1)*h*(tab5[i,l]));
end;
end;
writeln;
writeln('--------------------------------------------');
for i:=0 to n do
begin
for j:=0 to n do
begin
write(tab4[i,j]:2:2,' ')
end;
writeln;
end;
writeln;
for i:=0 to n do
begin
for j:=0 to n do
begin
write(tab5[i,j]:2:2,' ')
end;
writeln;
end;
writeln('------------------------------------------');
for p:=n downto 1 do
begin
for i:=p downto 1 do
begin
k:=trunc(tab4[i-1,p]);
v:=tab4[i-1,p]-k;
if(k<0) then
begin
k:=k*(-1);
tab4[i-1,p]:=tab4[i-1,p]*(-1);
end;
for j:=1 to k do
begin
tab4[i-1,p]:=tab4[i-1,p]-1;
for m:=0 to n do
tab5[i-1,m]:=tab5[i-1,m]-tab5[i,m];
end;
if(v<>0) then
begin
tab4[i-1,p]:=tab4[i-1,p]-v;
for m:=0 to n do
tab5[i-1,m]:=tab5[i-1,m]-v;
end;
end;
end;
writeln;
for i:=0 to n do
begin
for j:=0 to n do
begin
write(tab4[i,j]:2:2,' ')
end;
writeln;
end;
writeln;
for i:=0 to n do
begin
for j:=0 to n do
begin
write(tab5[i,j]:2:2,' ')
end;
writeln;
end;
writeln;}
readkey;
end;
4. Wnioski:
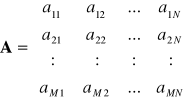
![]()
Wyszukiwarka
Podobne podstrony:
8419
8419
8419
więcej podobnych podstron