Obliczenia.
obliczam częstotliwość oraz okres drgań generatora wzorcowego
długość fali λ= 4 [cm]
V=![]()
λ=V⋅T => ![]()
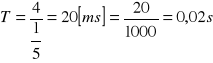
![]()
obliczam częstotliwość drgań dla każdej krzywej Lissajous oraz położenie skali
Wzór na częstotliwość drgań : ![]()
f0 - częstotliwość generatora wzorcowego
n1 - ilość pkt. styczności z osią y
n2 - ilość pkt. styczności z osią x
1. Położenie skali 1,11⋅100=111
![]()
2. Położenie skali 0,63⋅100=63
![]()
3. Położenie skali 1,70⋅100=170
![]()
4. Położenie skali 0,85⋅100=85
![]()
5. Położenie skali 0,85⋅100=85
![]()
6. Położenie skali 0,47⋅100=47
![]()
Obliczanie błędów.
1) Błąd częstości wzorcowej.
λ= 4[cm] ![]()
Δλ= ±0,2 T=0,02 s V=![]()
f = 50 [Hz]
![]()
![]()
![]()
![]()
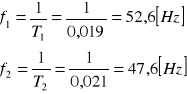
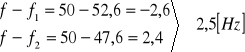
błąd częstości drgań generatora RC
1.
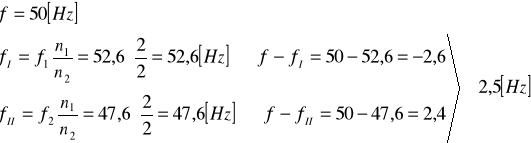
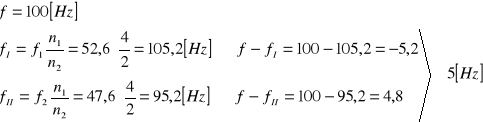
2.
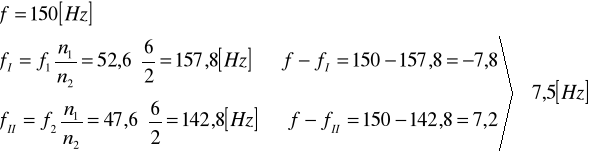
3.
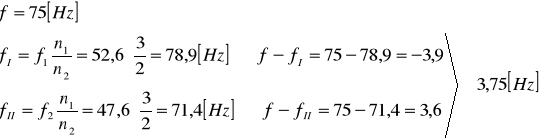
4.
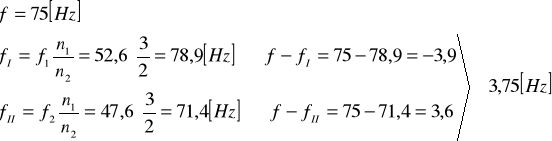
5.
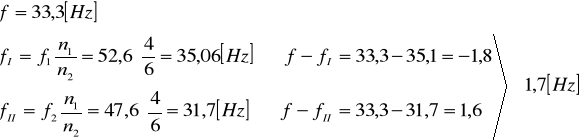
6.
IV. Wnioski:
Celem ćwiczenia jest zapoznanie się z zasadą pomiaru częstości drgań za pomocą oscyloskopu katodowego. W wyniku przeprowadzonego doświadczenia uzyskano figury Lissajous.
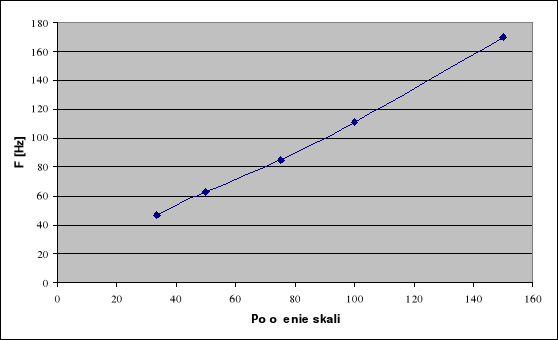
Powyższa metoda wyznaczania nieznanej częstości drgań jest metodą dość szybką i prostą w wykonaniu lecz nie jest to metoda zbyt dokładna. Występują tu błędy przy wyznaczaniu częstości. Błędy te nie są jednak znaczne, co można stwierdzić na podstawie wykresu. Występujące błędy są spowodowane m.in. złym odczytem ze skali milimetrowej ekranu, a co za tym idzie niedokładne wyznaczanie okresu i częstotliwości drgań generatora wzorcowego, a następnie pociąga to za sobą niedokładne wyznaczanie częstotliwości drgań dla każdej krzywej Lissajous. Błędów tych można by uniknąć, gdybyśmy dysponowali bardziej nowoczesnym oscyloskopem i generatorem, bowiem trudno było zatrzymać generator w celu przerysowania krzywych i wyznaczeniu ich parametrów.
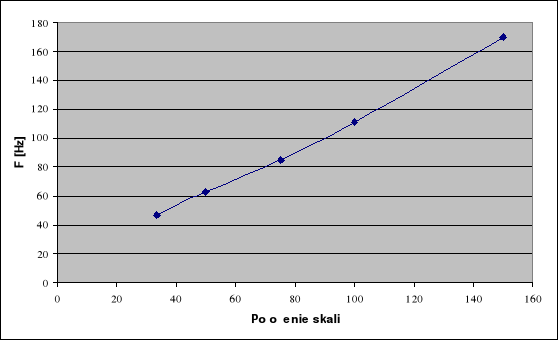
Wykres zależności częstości od liczb na skali generatora RC.
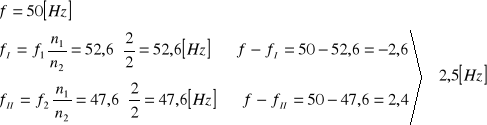
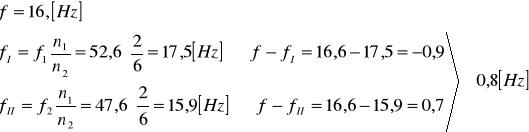
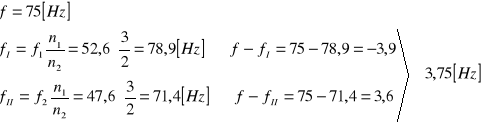
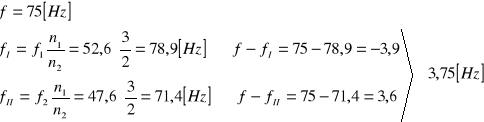
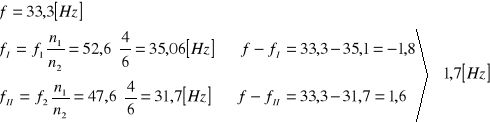
Wyszukiwarka
Podobne podstrony:
Drgania elektryczne, Sprawozdania - Fizyka
Drgania relaksacyjne 2, Sprawozdania - Fizyka
Pomiar częstotliwości drgań generatora przy użyciu oscyloskopu katodowego, Sprawozdania - Fizyka
Drgania relaksacyjne, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, sprawozd, Fizyka
Obliczenia Ogniwa, Sprawozdania - Fizyka
Drgania relaksacyjne3, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, sprawozd, Fizyka
Drgania obwodu LC, Politechnika Lubelska, Studia, Studia, Sprawozdanka, Fizyka 1, Bajcik.ver
obliczenia poprawione, Studia, Semestr 1, Fizyka, Sprawozdania, Sprawka, ćwiczenie 22 przyjęte
5 W DRGANIA RELAX MOJE , Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium,
OGNIWA (2), Sprawozdania - Fizyka
Ćwiczenie nr 50b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr50b
Mech- Badanie zależności współczynnika lepkości cieczy od te, Sprawozdania - Fizyka
Doświadczalne spr p. Malusa, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr70
Drgania tlumione wahadlo, Fizyka, FIZYKA, Fizyka ćwiczenia Miszta, Fizykaa, LabFiz1 od izki, LabFiz1
Sprawozdanie Fizyka ćwiczenie 4(M04)
ćw13 sprawozdania fizyka 3, Sprawozdanie
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
więcej podobnych podstron