Robert Maniura

Sprawozdanie z ćwiczenia nr B-8: Parachora.

1. Wstęp teoretyczny:

Rezultatem oddziaływań międzycząsteczkowych na granicy rozdziału fazy gazowej i ciekłej jest napięcie powierzchniowe cieczy. Wielkością fizyczną charakteryzującą powierzchnię rozdziału faz jest współczynnik napięcia powierzchniowego. Wartość liczbowa napięcia powierzchniowego jest określona wzorem:

gdzie: W - praca niezbędna do zwiększenia w procesie izotermicznym pola powierzchni rozdziału faz o S. Jednostką napięcia powierzchniowego w układzie SI jest niuton na metr (N/m).

Wartość napięcia powierzchniowego zależy w istotny sposób od rodzaju substancji i temperatury. Ze wzrostem temperatury napięcie powierzchniowe maleje (zależność ta jest zwykle liniowa), stając się równe zeru w temperaturze krytycznej.

Zdolność do zmniejszania napięcia powierzchniowego nazywa się aktywnością powierzchniową. Substancje wykazujące taką właściwość nazywa się powierzchniowo czynnymi lub powierzchniowo aktywnymi.

Molowa energia powierzchniowa  jest to energia napięcia powierzchniowego 1 mola cieczy pod postacią kuli. Pochodna molowej energii powierzchniowej powinna być stała dla wszystkich cieczy i niezależna od temperatury (Eötvös). Wówczas jest zajmowana najmniejsza swobodna powierzchnia:

gdzie: M- masa molowa [kg/mol]; d- gęstość [kg/m³]

Pochodna energii napięcia powierzchniowego wynosi:

gdzie: k- stała Eötvösa, równa 2,12.

W cieczach, w których występują wiązania wodorowe (asocjacja) wartość k jest mniejsza od 2,12.

Parachora łączy zależność między gęstością i napięciem powierzchniowym cieczy.

gdzie; c- stała dla danej substancji; d_c- gęstość cieczy [kg/m³]; d_p- gęstość pary [kg/m³]

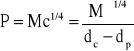
d_p jest mała w porównaniu z d_c - można ją ominąć. Wtedy:

gdzie: V- objętość molowa cieczy [m³/mol]

Parachora wykazuje właściwości addytywne. Do całkowitej wartości parachory swój wkład wnoszą poszczególne atomy, wiązania i ugrupowania atomów.

2. Opracowanie wyników:

Celem ćwiczenia jest wyznaczenie napięcia powierzchniowego czystej cieczy i sprawdzenie reguły addytywności parachory.

Pomiaru napięcia powierzchniowego dokonuję za pomocą stalagmometru. Pomiar polega na zmierzeniu liczby kropli, które wypływają z objętości zawartej między kreskami pomiarowymi stalagmometru dla badanej cieczy i wody. Napięcie powierzchniowe wyznacza się z odpowiedniego równania. Gęstość badanej cieczy wyznacza się za pomocą piknometru. Na podstawie znalezionego napięcia powierzchniowego oblicza się wartość parachory.

Gęstość metanolu wyznaczona metodą piknometryczną:

gdzie: d - gęstość metanolu [g/cm³]; m_s - masa piknometru wypełnionego metanolem [g]; m_w - masa piknometru wypełnionego wodą [g]; m₀ - masa pustego piknometru [g]; d_H2O - gęstość wody w temperaturze pomiaru [g/cm³] - w 18 °C wynosi 0,99843 g/cm³.

Gęstość metanolu wynosi 0,79469 g/cm³ = 794,69 kg/m³.

Błąd wyznaczenia gęstości metanolu obliczony metodą różniczki zupełnej:

gdzie: m_m - masa metanolu w piknometrze [kg]; m_w - masa wody w piknometrze [kg]; d_w - gęstość wody w temperaturze pomiaru [kg/m³];

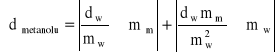
gdzie:  m_w = 0,1*10^-3 kg; m_m = 0,1*10^-3 kg; d_w = 998,43 kg/m³; m_w = 3,3314*10^-3 kg; m_m = 2,6516*10^-3 kg;

 d_b = 53,82 kg/m³

Gęstość metanolu wynosi 794,69 ± 53,82 kg/m³.

Napięcie powierzchniowe metanolu przedstawia następujący wzór:

gdzie: Z - ilość kropel; d - gęstość (kg/m³); σ - napięcie powierzchniowe (N/m); w - woda; m - metanol.

Do powyższego wzoru wstawiam następujące dane: Z_m = 69,14; Z_w = 28,14; σ_w = 72,75*10^-3 N/m; d_w = 998,43 kg/m³; d_m = 794,69 kg/m³

Błąd wyznaczonego napięcia powierzchniowego:

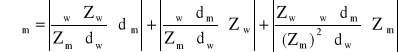
gdzie: Z_m = 69,14; Z_w = 28,14; σ_w = 72,75*10^-3 N/m; d_w = 998,43 kg/m³; d_m = 794,69 kg/m³;  Z_w = 1;  Z_m = 1;  d_m = 53,82 kg/m³.

σ_m  2,80*10^-3 N/m

Napięcie powierzchniowe wynosi σ_m = 23,57*10^-3±2,80*10^-3 N/m.

Molowa energia powierzchniowa dla metanolu w oparciu o znalezione napięcie powierzchniowe i gęstość:

gdzie: σ_m = 23,57*10^-3 N/m; M_m = 32,04*10^-3 kg/mol; d_m = 794,69 kg/m³

Po podstawieniu do równania:

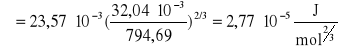
Błąd wyznaczenia molowej energii powierzchniowej:

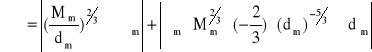
gdzie: M_m = 32,04*10^-3 kg/mol; σ_m = 23,57*10^-3 N/m; σ_m = 2,80*10^-3 N/m; d_m = 794,69 kg/m³;  d_m = 53,82 kg/m³

 = 0,20*10^-5 J/mol^2/3

Molowa energia powierzchniowa wynosi:  = 2,77*10^-5 ± 0,20*10^-5 J/mol^2/3.

Pochodna molowej energii powierzchniowej względem temperatury powinna być stała dla wszystkich cieczy i niezależna od temperatury.

W temperaturze krytycznej T_K napięcie powierzchniowe zanika całkowicie. Całkując powyższe równanie dostaje się zależność:

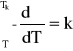
;  = k (T_k - T) gdzie: T_k - temperatura krytyczna metanolu = 513,15 K; T- temperatura pomiaru = 291,15 K;  - molowa energia powierzchniowa.

Ponieważ zanik napięcia powierzchniowego następuje w temperaturze o kilka stopni niższej od temperatury krytycznej lepiej jest spełniona zależność:

 = k(T_k - T - 6)

skąd stała k wynosi:

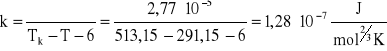
Błąd stałej równania Eötvösa:

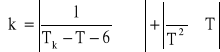
gdzie: T = 1 K;  = 0,20*10^-5; T_K = 513,15 K;  = 2,77*10^-5 J/mol^2/3; T = 291,15 K

Dk = 0,10*10^-7

Stała Eötvösa k = 1,28*10^-7±0,10*10^-7[J/(mol^2/3*K].

Obliczona wartość parachory na podstawie wyznaczonego napięcia powierzchniowego oraz gęstości metanolu:

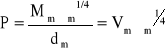
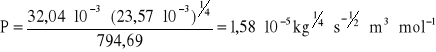
Błąd wyznaczenia parachory:

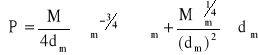
; M = 32,04*10^-3 kg/mol; σ_m = 23,57*10^-3 N/m; σ_m = 2,80*10^-3 N/m; d_m = 794,69 kg/m³; d_m = 53,82 kg/m³

P = 0,20*10^-5[kg^1/4 * s^-1/2 * m³ * mol^-1]

Wartość parachory P = 1,58*10^-5 ± 0,20*10^-5 [kg^1/4 * s^-1/2 * m³ * mol^-1].

Wartość parachory obliczona teoretycznie na podstawie addytywności. Cząsteczka metanolu zawiera:

• 1 atom węgla

• 3 atomy wodoru

• 1 grupa wodorotlenowa

P = 1*P_C + 3*P_H + 1*P_OH; gdzie: P_C =0,85 * 10^-6[kg^1/4 * s^-1/2 * m³ * mol^-1]; P_H = 3,04*10^-6[kg^1/4 * s^-1/2 * m³ * mol^-1]; P_OH = 5,74*10^-6[kg^1/4 * s^-1/2 * m³ * mol^-1];

P = 0,85*10^-6 + 3*3,04*10^-6 +5,74*10^-6 = 1,571*10^-5[kg^1/4 * s^-1/2 * m³ * mol^-1]

Zestawienie wyników pomiarów i obliczeń dla metanolu:

L.p.	Wielkość i jednostka	Wartość	Błąd
1	Masa molowa [kg/mol]	32,04*10^-3	---
2	Gęstość [kg/m^3]	794,69	53,82
3	Napięcie powierzchniowe [N/m]	23,57*10^-3	2,80*10^-3
4	Temp krytyczna [K]	513,15	---
5	Molowa energia powierzchniowa [J/mol^2/3]	2,77*10^-5	0,20*10^-5
6	Stała Eötvösa [J/(mol^2/3*K)]	1,28*10^-7	0,10*10^-7
7	Parachora wyznaczona [kg^1/4s^-1/2 m^3 mol^-1]	1,58*10^-5	0,20*10^-5
8	Parachora obliczona [kg^1/4s^-1/2 m^3 mol^-1]	1,571*10^-5	---

4. Wnioski:

Wyznaczona doświadczalnie wartość parachory jest w dobrej zgodności z wartością parachory wyznaczonej teoretycznie na podstawie parachor atomowych. Powstałe rozbieżności pomiędzy wynikami uzyskanymi doświadczalnie a wynikami uzyskanymi w obliczeniach teoretycznych mogły być spowodowane niedokładnościami związanymi z ważeniem podczas wyznaczania gęstości przy pomocy piknometru. Innym źródłem niedokładności mogły być błędy związane z liczeniem wypływających kropli, a także z niedokładnościami odmierzania objętości cieczy. Na podstawie uzyskanych wyników doświadczenia, i ich zgodności z wartością parachory wyznaczonej teoretycznie można potwierdzić, iż parachora jest wielkością addytywną, i można ją rozłożyć na składowe pochodzące od poszczególnych atomów, wiązań czy szczególnych ugrupowań atomowych.

5. Literatura:

Kazimierz Gumiński „Wykłady z chemii fizycznej”.

Witold Mizerski „Tablice chemiczne”.

Kalendarz chemiczny.

1

---