Michał Sobczak 13.10.05 r.

WTD I czwartek

Mechanika 14-17

Ćwiczenie nr 8

Cel ćwiczenia

Celem ćwiczenia jest określenie momentu bezwładności bryły metalowej. Dokonamy tego stosując metodę wahadła fizycznego. Polega ona na pomiarach okresu drgań wahadła (czyli bryły której moment bezwładności próbujemy zbadać), zawieszonego na poziomej, poprzecznej osi.

I. Wstęp teoretyczny

Moment bezwładności to miara bezwładności ciała w ruchu obrotowym. Im większy moment tym trudniej rozkręcić dane ciało.

gdzie:

• m - masa fragmentów ciała oddalonych o osi obrotu o długość r

• r - odległość fragmentów ciała od jego osi obrotu

Częstotliwość określa liczbę cykli zjawiska okresowego występujących w jednostce czasu. W układzie SI jednostką częstotliwości jest herc (Hz). Częstotliwość 1 herca odpowiada występowaniu jednego zdarzenia (cyklu) w ciągu 1 sekundy.

gdzie:

• T- okres,

• f - częstotliwość

Prędkość to wektorowa wielkość fizyczna wyrażająca zmianę położenia w czasie. Jej wartością jest szybkość. Jednostką prędkości w układzie SI to m/s

Izochronizm wahadła to niezależność okresu drgań wahadła od amplitudy drga tego wahadła.

Twierdzenie Steinera opisuje, w jaki sposób znaleźć moment bezwładności danej bryły względem danej osi, jeżeli znany jest moment bezwładności względem osi równoległej i przechodzącej przez środek bryły.

I = I₀ + md²

gdzie:

• I₀ - moment bezwładności względem osi przechodzącej przez środek masy

• I - moment bezwładności względem osi równoległej

• d - odległość między osiami

• m - masa bryły

I zasada dynamiki Newtona:

Jeżeli na ciało nie działa żadna siła lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym (po prostej ze stałą prędkością).

II zasada dynamiki Newtona:

Przyspieszenie z jakim porusza się ciało jest proporcjonalne do działającej siły i odwrotnie proporcjonalne do masy ciała. Kierunek i zwrot przyspieszenia jest zgodny z kierunkiem i zwrotem siły.

III zasada dynamiki Newtona

Jeśli ciało A działa na ciało B siłą F (akcja), to B działa na A siłą (reakcja) o takiej samej wartości i kierunku, lecz o przeciwnym zwrocie.

Schemat doświadczenia:

Na początek należy zmierzyć wartość wewnętrznego promienia bryły. Bryłę zawieszamy na osi tak, aby punkt podparcia znajdował się powyżej środka ciężkości bryły. Wahadło odchylamy o niewielki kąt od położenia spoczynku i puszczamy(wprawiamy w ruch drgający wahadłowy). Następnie mierzymy czas kilkudziesięciu pełnych wahnięć bryły. Pomiar ten należy powtórzyć trzykrotnie i obliczyć średni okres drgań. Mając te dane jesteśmy gotowi do obliczenia momentu bezwładności, rachunku błędów i zakończenia doświadczenia.

II. Obliczenia

Średni promień obręczy - 0,105 m

Czas jednego okresu - 0,9195 s

Przyspieszenie ziemskie:

Moment bezwładności:

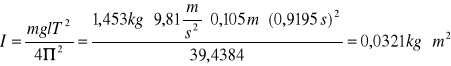
Rachunek błędu dla obręczy:

błąd bezwzględny:

błąd procentowy:

średni promień koła-oś1 - 0,016 m

czas jednego okresu - 1,1065 s

moment bezwładności:

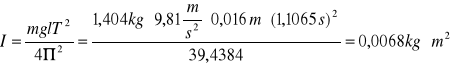
rachunek błędu dla koła-oś1:

błąd bezwzględny:

błąd procentowy:

średni promień koła-oś2 - 0,065 m

czas jednego okresu - 0,7436 s

moment bezwładności:

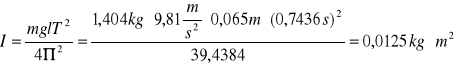
rachunek błędu dla koła-oś2:

błąd bezwzględny:

błąd procentowy:

III. Wnioski i spostrzeżenia

Wynik z błędem dla obręczy:

Wynik z błędem dla koła-oś1:

Wynik z błędem dla koła-oś2:

Cel ćwiczenia został osiągnięty. Momenty bezwładności brył (obręczy i koła) zostały określone. Pomiary zostały wykonane na tyle dokładnie na ile pozwala dokładność przyrządów mierniczych i ludzka percepcja. Błędy procentowe mieszczą się w przedziale 0,37-1,02% czyli stosunkowo niskim, prawie niezauważalnym. Wnioskować można, że przy podobnej masie przedmioty o różnym rozmieszczeniu masy i różnych osiach mają różne wyniki bezwładności. Im bliżej oś obrotu znajduje się środka ciężkości tym mniejszy jest moment bezwładności.

1