6. Teoria liczb

Teoria liczb jest dziedziną matematyki, zajmującą się badaniem własności liczb - początkowo tylko całkowitych, a obecnie algebraicznych, przestępnych, p-adycznych. W starożytności zajmowali się nią Pitagoras, Euklides, Eratostenes, Diofantos i wielu innych. Rozwój teorii liczb spowodowany został przez Pierre'a Fermata (1601-1665), autora słynnej hipotezy, zwanej Wielkim Twierdzeniem Fermata..

Badania w zakresie teorii liczb przyczyniły się do znacznego rozwoju wielu gałęzi matematyki: algebry, teorii funkcji zmiennej zespolonej, rachunku prawdopodobieństwa, geometrii algebraicznej i innych.

Najstarszym działem teorii liczb jest elementarna teoria liczb, w której nie stosuje się metod teorii funkcji analitycznych. Teoria liczb zajmuje się również rozwiązywaniem równań w dziedzinie liczb naturalnych, całkowitych (tzw. równania diofantyczne), wymiernych.

Podzielność w zbiorze liczb całkowitych

Niech a, b będą liczbami całkowitymi i a≠0 (a∈Z\{0},b∈Z).

Mówimy, że liczba a dzieli liczbę b (a jest dzielnikiem b, a jest czynnikiem b), jeżeli istnieje taka liczba całkowita c, że b=a⋅c, co oznacza się symbolem ab.

ab ⇔ ∃c∈Z b=a⋅c.

Podzielność jest relacją binarną w zbiorze liczb całkowitych Z.

Jeżeli a,b,c∈Z ∧ ca ∧ cb ⇒ c jest wspólnym dzielnikiem a i b.

Jeżeli a,b,c∈Z to zachodzą następujące własności relacji ab:

1. 1a, ponieważ a=1⋅a oraz a0, ponieważ 0=a⋅0;

2. aa, ponieważ a=a⋅1;

3. ab⇒ (-a)b ∧ a(-b);

4. ab∧ bc⇒ ac;

5. ab∧ ba⇒a=b∨a=-b;

6. ab⇒∀x∈Z abx;

7. ab⇒∀x∈Z\{0} axbx;

8. ab∧ ac⇒∀x,y∈Z a(bx+cy).

Definicja i własności liczb pierwszych

Liczbę naturalną p>1, której jedynymi dzielnikami w zbiorze N są 1 i p, nazywamy liczbą pierwszą. Liczby naturalne, które nie są liczbami pierwszymi nazywamy liczbami złożonymi.

Najmniejszy dodatni i różny od zera dzielnik liczby całkowitej jest liczbą pierwszą.

Istnieje nieskończenie wiele liczb pierwszych.

Liczba naturalna p>1 jest liczbą pierwszą wtedy i tylko wtedy, gdy dla dowolnych dwóch liczb naturalnych a i b zachodzi implikacja

p(a⋅b) ⇒ pa ∨ pb.

Twierdzenie o liczbach pierwszych

Niech funkcja π(x) oznacza liczbę liczb pierwszych nie większych od x. Wtedy prawdziwa jest zależność:

Z równości tej wynikają następujące zależności:

1. Dla x≥17
   

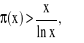
2. Dla x>1
   

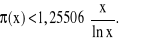
Podstawowe twierdzenie elementarnej teorii liczb

Każdą liczbę naturalną n>1 można przedstawić jako iloczyn naturalnych potęg liczb pierwszych:

Przedstawienie to zwane faktoryzacją jest jednoznaczne z dokładnością do uporządkowania czynników.

Największym wspólnym dzielnikiem (greatest common divisor) liczb całkowitych a i b jest dodatnia liczba naturalna d oznaczana NWD(a,b) lub gcd(a,b) taka, że

- d jest wspólnym dzielnikiem a i b

- ca ∧ cb⇒cd.

Przyjmuje się, że NWD(0,0)=0.

Liczby całkowite a i b nazywamy względnie pierwszymi jeżeli NWD(a,b)=1.

Najmniejszą wspólną wielokrotnością (least common multiple) liczb całkowitych a i b jest dodatnia liczba naturalna d oznaczana NWW(a,b) lub lcm(a,b) taka, że

- ad ∧ bd,

- ac ∧ bc⇒dc.

Dla dodatnich liczb całkowitych a i b zachodzi zależność:

Jeżeli liczby a i b przedstawimy w postaci

to

Funkcja Eulera φ

Dla danej liczby naturalnej n funkcja Eulera φ(n) określa liczbę liczb naturalnych nie większych od n i względnie pierwszych z n.

Własności funkcji Eulera φ:

Jeżeli p i q są liczbami pierwszymi to:

φ(p)=p-1; φ(p^k)=p^k-1(p-1);

φ(pq)=(p-1)(q-1).

Jeżeli a i b są względnie pierwsze to φ(a⋅b)=φ(a)⋅φ(b).

Dla liczb naturalnych n≥5 zachodzi nierówność:

Jeżeli

jest rozkładem liczby n na czynniki pierwsze to

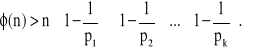
Jeżeli a, b są liczbami całkowitymi (a,b∈Z) i ponadto b≥1, to można określić dzielenie liczby a przez liczbę b, które w wyniku daje iloraz q oraz resztę r co zapisujemy:

a=q⋅b+r

przy czym 0≤r<b oraz q i r wyznaczone są jednoznacznie.

Stosuje się oznaczenia r=a mod b oraz q=a div b.

Jeżeli a,b∈Z ∧ b≥1 ⇒ a div b=a/b ∧ a mod b=a-b⋅a/b.

Algorytm Euklidesa do wyznaczania NWD(a,b)

Jeżeli a, b są liczbami naturalnymi i a≥b to zachodzi następująca własność NWD(a,b)=NWD(b,a mod b).

Pseudokod algorytmu:

while (b≠0) do

{

r:=a mod b;

a:=b;

b:=r;

}

return (a)

Rozwiązywanie równań diofantycznych postaci ax+by=c

Równanie a'x+b'y=c ma rozwiązanie w liczbach całkowitych wtedy i tylko wtedy, gdy NWD(a',b') dzieli c. Można więc to równanie podzielić przez NWD(a',b') doprowadzając do postaci:

ax+by=d.

Rozszerzony algorytm Euklidesa umożliwia rozwiązywanie równań postaci ax+by=d, w których d=NWD(a,b).

Pseudokod rozszerzonego algorytmu Euklidesa:

Ext_Euclid (a,b)

{

if (b=0)

then return (a,1,0);

(d',x',y'):=Ext_Euclid (b,a mod b)

(d,x,y):=(d',y',x'-a/by';

return (d,x,y):

}

Kongruencje

Niech n∈N⁺. W zbiorze Z określmy relacje oznaczaną ≡ (mod n) następująco:

a≡b (mod n) ⇔ n(a-b).

Własności relacji

1. a≡a (mod n),

2. a≡b (mod n) ⇒ b≡a (mod n),

3. a≡b (mod n) ∧ b≡c (mod n) ⇒ a≡c (mod n),

4. a≡b (mod n) ⇒ a mod n=b mod n,

5. a≡b (mod n) ∧ rn ⇒ a≡b (mod r),

6. a≡b (mod n) ∧ a≡b (mod m) ∧ NWD(n,m)=1⇒ a≡b (mod nm),

Relacja ta jest relacją równoważności w Z, więc dzieli zbiór Z na klasy abstrakcji:

[0]_{≡(mod n)}={z∈Zz mod n=0},

[1]_{≡(mod n)}={z∈Zz mod n=1},

[2]_{≡(mod n)}={z∈Zz mod n=2},

…

[n-1]_{≡(mod n)}={z∈Zz mod n=n-1}.

Zbiór Z_n={0,1,2,…,n-1} nazywamy zbiorem liczb całkowitych modulo n.

W zbiorze tym określone są działania dodawanie, odejmowanie i mnożenie wykonywane modulo.

Relacja mod n jest kongruencją w Z dla działań dodawania, odejmowania oraz mnożenia. Nazywamy ją więc kongruencją w Z.

---