Podstawą naszych obliczeń była funkcja wyrażona wzorem:

y= (x₁-A)² + (x₂+B)² + C

gdzie:

A= 9

B= 12

C= 89

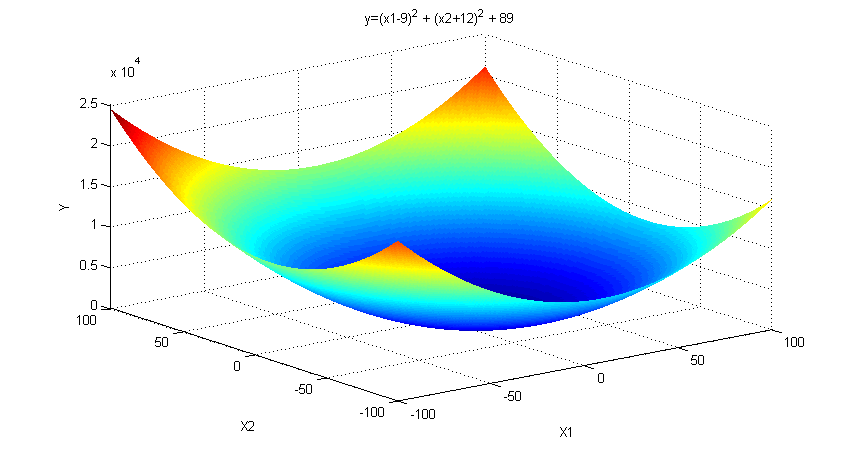
1. Wykres funkcji
   
   Aby stworzyć wykres funkcji, przyjęliśmy przedziały argumentów:
   x1=[-100:100]
   x2=[-100:100]
   
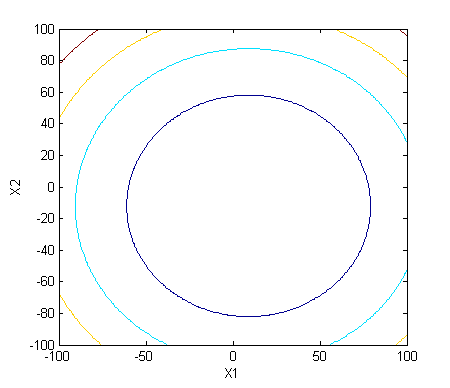
   Poniższy fragment kodu spowodował wyświetlenie 2 wykresów:
   -trójwymiarowego wykresu wywołanego funkcja surf
   -wykresu poziomicowego - funkcja contour

A=9;

B=12;

C=89;

n1=100;

n2=-100;

x1=[-n1:n1];

x2=[-n1:n1];

[X1,X2]=meshgrid(x1,x2);

y=(X1-A).^2+(X2+B).^2+C;

figure(1)

surf(X1,X2,y);

shading flat

grid

figure(2)
contour(X1,X2,y);

2. Znalezienie minimum funkcji.
   
   Do znalezienia minimum wykorzystaliśmy funkcję fminsearch:

fun = @ (X) (X(1)-A).^2+(X(2)+B).^2+C;

[min, fval] = fminsearch (fun, [-1, 1]);

min

fval

Wykonanie powyższego kodu spowodowało wyświetlenie współrzędnych:
min =

9.0000 -12.0000

oraz wartości minimum funkcji:

fval =

89.0000

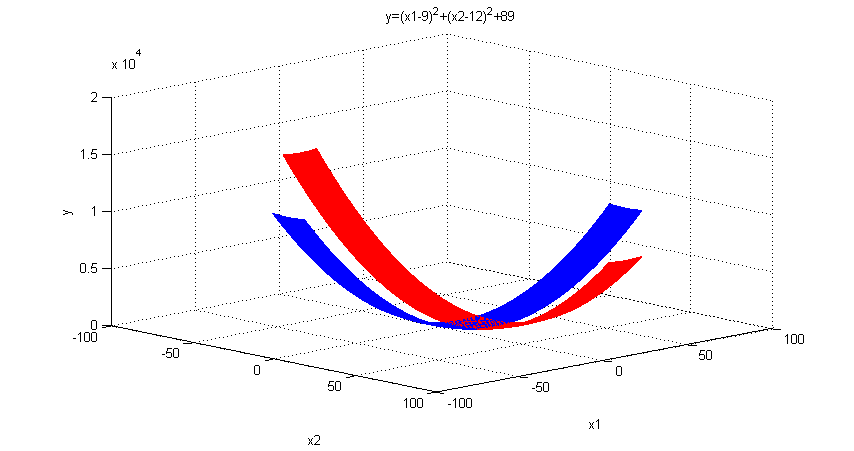
3. Przecięcie wykresu płaszczyznami

Celem tej części zadania było przecięcie wykresu funkcji w punkcie minimum 2 płaszczyznami prostopadłymi do siebie i płaszczyzny x1-x2. Wynikiem takiego działania są 2 przecinające się w punkcie minimum parabole. Przyjęliśmy tolerancję 10%


zb1=[A-10,A+10,n1,n2];

zb2=[n1,n2,B-10,B+10];

figure(3)

hold on

ezsurf('(x-9).^2+(y-12).^2+89',zb1);

ezsurf('(x-9).^2+(y-12).^2+89',zb2);

grid;

hold off