PRACA DOMOWA NR 9 Z MATEMATYKI (Logistyka, studia dzienne, I rok)

Zad. 1. Wyznaczyć granice funkcji, korzystając z reguły de L'Hospitala:

a)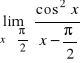
, b)
, c)
, d)
, e)
, f)
, g)
, h)
, i)
.

Wskazówka do zad. 1h), i): regułę de L'Hospitala należy w tych przykładach zastosować dwukrotnie

Zad. 2. Wyznaczyć równanie stycznej do wykresu funkcji
w punkcie o odciętej
.

Zad. 3. Wyznaczyć równanie stycznej do wykresu funkcji
, nachylonej do osi
pod kątem
.

Zad. 4. Wyznaczyć równanie stycznej do wykresu funkcji
, równoległej do prostej
.

Zad. 5. Wyznaczyć równanie stycznej do wykresu funkcji
, prostopadłej do prostej
.

Zad. 6. Wyznaczyć równanie stycznej do wykresu funkcji
w punkcie przecięcia tego wykresu z osią
.

Odpowiedzi do zadań:

Zad. 1: a)
, b)
, c)
, d)
, e)
, f)
, g)
, h)
, i)
;

Zad. 2:
;

Zad. 3: są dwie takie styczne:
,
;

Zad. 4:
;

Zad. 5:
;

Zad. 6:
.

---