Oblicz granicę:
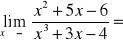
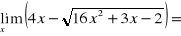
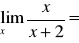
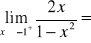
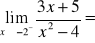
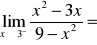
Oblicz granicę
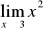
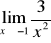
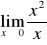
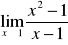
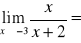
Dana jest funkcja
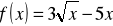
określ jej dziedzinę,
oblicz pochodną,
określ dziedzinę pochodnej.
Oblicz pochodną funkcji
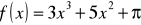
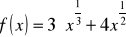
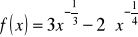
.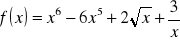
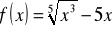
,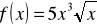
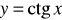
,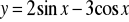
,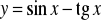
.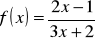
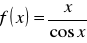
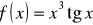
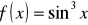
Wyznacz przedziały monotoniczności funkcji
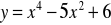
,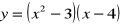
,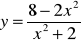
.Wyznacz ekstrema funkcji
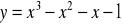
,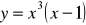
.Wyznacz kąt nachylenia do osi OX stycznej do krzywej
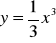
w punkcie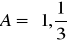
.Wyznacz współczynnik kierunkowy stycznej do krzywej
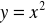
w punkcie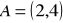
.Napisz równanie stycznej do paraboli
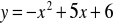
w punkcie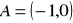
.Dana jest funkcja
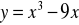
wyznacz dziedzinę funkcji,
oblicz miejsca zerowe,
wyznacz przedziały monotoniczności,
wyznacz ekstrema funkcji.
Dana jest funkcja
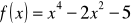
,wyznacz przedziały monotoniczności funkcji
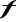
,znajdź ekstrema funkcji.
Zbadaj przebieg zmienności funkcji
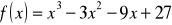
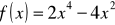
i naszkicuj jej wykres.
Z drutu długości 80 cm zrobiono ramkę w kształcie prostokąta. Jakie wymiary powinien mieć prostokąt, aby jego pole było maksymalne?
Podaj, jakie wymiary powinien mieć otwarty prostopadłościenny zbiornik o objętości 32 m3 i głębokości 2 m, aby pole powierzchni całkowitej tego zbiornika było minimalne.
Jakie wymiary powinien mieć prostokąt o danym obwodzie
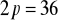
cm, aby walec który powstaje z obrotu tego prostokąta dookoła jednego z boków miał największą objętość?Naczynie w kształcie stożka ma tworzącą o długości równej l = 10 cm. Dobierz wysokość tego naczynia tak, aby jego pojemność była maksymalna.
Wyszukiwarka
Podobne podstrony:
Granica funkcji(1), Prywatne
lista7 granica, ciaglosc i pochodna funkcji
granica funkcji zadania 1 plus 2
Analiza matematyczna Wykłady, GRANICE FUNKCJI
Matematyka cw5 Granice funkcji Ciaglosc funkcji Asymptoty
twierdzenia o funkcjach z pochodnymi
Granice funkcji
granice funkcji ciaglosc funkcji (1)
Granica funkcji w punkcie
07 funkcje zmiennej rzeczywistej 3 2 granica funkcji
GRANICE FUNKCJI
8 Zadania do wykladu Granica funkcji Ciaglosc funkcji 1
Arkusz nr 3 (Granice funkcji)
2010 12 10(2) granica funkcji, ciągłość funkji, różniczkowalność, iloraz różnicowy
Analiza matematyczna. Wykłady GRANICE FUNKCJI
Granica funkcji, Granica funkcji
Kolokwium granice i funkcja
więcej podobnych podstron