PAWEŁ WETKLO

RAFAŁ KMIECIK

ĆWICZENIE 14

WYZNACZANIE STAŁEJ RÓWNOWAGI REAKCJI

I₂ + I^- = I^-₃

CEL ĆWICZENIA

Celem ćwiczenia jest ustalenie stałej równowagi reakcji:

I₂ + I^-
I^-₃

i wykazanie, że wielkość ta nie zależy od stężenia reagentów w roztworze.

WSTĘP

RÓWNOWAGA CHEMICZNA - mówimy, że układ znajduje się w stanie równowagi wtedy, gdy nie występują w nim przepływy masy i energii, parametry stanu zachowują w czasie wartości stałe, a stan ten nie ulega zmianie przy zmianie warunków zewnętrznych.

W chwili osiągnięcia równowagi chemicznej szybkość reakcji pierwotnej staje się równa szybkości reakcji odwrotnej. Z tego warunku wyprowadza się stałą równowagi chemicznej metodami kinetyki chemicznej. Większość reakcji prowadzi się w warunkach

T,p = const.

Przebiegowi izotermicznej i izobarycznej reakcji chemicznej typu
towarzyszy zmiana potencjału chemicznego układu, którą ogólnie można przedstawić równaniem

(1)

prod. substr.

gdyż w układzie znikają substraty (v_i<0), a na ich miejsce powstają stechiometryczne ilości produktów (v_i>0). Równanie to jest słuszne dla
= 1. Warunek równowagi, dla przemian izotermiczno - izobarycznych, przy braku pracy nieobjętościowej, brzmi
= 0. Wobec tego równanie (1) zapisujemy następująco

(2)

Potencjał chemiczny reagenta jest związany z jego aktywnością.

(3)

Podstawiając tę zależność do równania (2) oraz wprowadzając pojęcie aktywności w stanie równowagi a_i^* , otrzymujemy:

(4)

stąd:

(5)

gdzie

- potencjał standardowy reakcji chemicznych.

W warunkach T,p = const. wartość tej funkcji jest stała. Dlatego możemy napisać:

K_a(T,p)= π(a_i^*)^v
(6)

Pamiętając, że v_i >0 dla produktów reakcji i v_i <0 dla substratów reakcji, z równania (6) wynika, że w warunkach T,p=const, w stanie równowagi, stosunek iloczynu substratów, jest wielkością stałą.

Równanie (5) definiuje termodynamiczną stałą równowagi chemicznej. Jeżeli aktywność zamienimy stężeniem, co jest słuszne tylko przy spełnieniu określonych warunków, wtedy otrzymamy klasyczne prawo równowagi chemicznej nazywane prawem działania mas. Jeżeli wprowadzimy stężenie objętościowe c [mol/dm³], wtedy:

K_c(T,p)=π
(7)

WYKONANIE ĆWICZENIA

Reakcję jodu z jonem jodkowym prowadzi się w dwóch roztworach, które różnią się stężeniem jodu. Stan równowagi tej reakcji ustala się szybko. Stężenie jodu w mieszaninie reakcyjnej oznacza się za pomocą miareczkowania roztworem tiosiarczanu sodowego. W ten sposób oznacza się całkowite stężenie jodu (I₂ + I^-₃) w roztworze wodnym, zgodnie z równaniami reakcji:

2S₂O₃^2- + I₂ = S₄O₆^2-

oraz

2S₂O₃^2-+ I^-₃ = S₄O₆^2- + 3I^-

Jony I^-₃ są nietrwałe i rozpadają się w czasie miareczkowania. W celu obliczenia stałej równowagi należy znać stężenie wolnego I₂ i stężenie jonu trójjodowego I^-₃ w stanie równowagi. Należy więc w odpowiedni sposób oznaczyć stężenie jednego z tych reagentów.

Stężenie wolnego jodu w mieszaninie reakcyjnej można wyznaczyć wykorzystując prawo podziału Nernsta. W tym celu wodny roztwór, w którym zachodzi reakcja chemiczna wytrząsa się z czterochlorkiem węgla. Praktycznie tylko I₂ rozpuszcza się w CCl₄ i przechodzi do warstwy organicznej w takich ilościach, że stosunek jego stężeń w obu warstwach równa się współczynnikowi podziału. W układzie ustala się równowaga dwóch procesów: równowaga reakcji chemicznej w roztworze wodnym, oraz równowaga podziału I₂ pomiędzy wodę i CCl₄. Stężenie I₂ w CCl₄ w stanie równowagi obu procesów oznacza się również za pomocą miareczkowania roztworem Na₂S₂O₃. Znając współczynnik podziału I₂ pomiędzy CCl₄ i wodę, oraz stężenie I₂ w warstwie czterochlorku węgla oblicza się stężenie wolnego I₂ w warstwie wodnej. Na tej podstawie można obliczyć stężenia reagentów oraz stałą równowagi.

WYKONANIE POMIARÓW

Do dwóch rozdzielaczy o pojemności 250 cm³ wprowadziliśmy następujące odczynniki:

rozdzielacz 1: 20cm³ nasyconego roztworu I₂ w CCl₄,

100cm³ 0,1 m KI

rozdzielacz 2: 10cm³ nasyconego roztworu I₂ w CCl₄,

10cm³ CCl₄,

100cm³ 0,1 m KI.

Zawartość rozdzielaczy wytrząsaliśmy się w ciągu 15 minut i umieściliśmy w łapach statywów na 30 minut. Następnie kolejno w każdym rozdzielaczu oznaczaliśmy stężenie jodu w obu warstwach. W tym celu z każdej warstwy pobraliśmy 3 próbki po 5cm³ roztworu.

Próbkę pobraną z warstwy organicznej wprowadziliśmy do kolbki zawierającej 10cm³ 0,1 m KI i roztwór miareczkowaliśmy za pomącą 0,01 n Na₂S₂O₃. Pod koniec miareczkowania, gdy roztwór jest lekko żółty dodaliśmy kilka kropli roztworu skrobi i miareczkowaliśmy do całkowitego odbarwienia.

Próbkę pobraną z warstwy wodnej miareczkowaliśmy roztworem tiosiarczanu sodowego bezpośrednio. Wyniki miareczkowania zanotowaliśmy.

OBLICZENIA I WNIOSKI

• stężenie molowe jodu w warstwie czterochlorkowej jodu

gdzie
- ilość ml Na₂S₂O₃ zużyta do miareczkowania próbki pobranej z warstwy czterochlorkowej.

1. Rozdzielacz

c=0,5·18,3·(0,01·10^-3·1000)/5=0,0183 [molI₂/dm³]

2. Rozdzielacz

c=0,5·9,2·(0,01·10^-3·1000)/5=0,0092 [molI₂/dm³]

• suma stężeń molowych jodu I₂ i jonów I^-₃ w warstwie wodnej

I Rozdzielacz

c=0,5·14,4·(0,01·10^-3·1000)/5=0,0144 [mol(I₂+I^-₃)/dm³]

II Rozdzielacz

c=0,5·7,3·0,01·10^-3·1000/5=0,0073 [mol(I₂+I^-₃)/dm³]

• stężenie wolnego jodu I₂ w warstwie wodnej

I Rozdzielacz

c=0,01·0,0183=0,000183=0,183·10^-3

II Rozdzielacz

c=0,01·0,0092=0,000092=0,092·10^-3

• stężenie molowe jonów I^-₃ w warstwie wodnej

I Rozdzielacz

c=0,0144-0,000183=0,014217=14,217·10^-3

II Rozdzielacz

c= 0,0073-0,000092=0,007208=7,208·10^-3

• stężenie molowe jonów jodkowych I^- w warstwie wodnej

C_oI^- =0.1 mol/dm³

I Rozdzielacz

c=0,1-0,014217=0,085783=85,783·10^-3

II Rozdzielacz

c=0,1-0,007208=0,092792=92,792·10^-3

• stałą równowagi obliczamy ze wzoru:

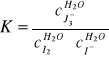
I Rozdzielacz

K=14,217·10^-3/(0,183·10^-3·85,783·10^-3)=905,6

II Rozdzielacz

K=7,208·10^-3/(0,092·10^-3·92,792·10^-3)=844,3

WNIOSKI

Stałe równowagi reakcji nie różnią się zbytnio od siebie, co świadczy, że stała równowagi jest wielkością charakterystyczną dla danej reakcji i jest niezależna od stężenia substancji reagujących (reagentów).

Niewielka różnica jest wynikiem użycia 10cm³ CCl₄ do reakcji zachodzącej w drugim rozdzielaczu.

TABELA WYNIKÓW

	ROZDZIELACZ I	ROZDZIELACZ II
n [ml/5ml próbki]	18,3	9,2
n [ml/5ml próbki]	14,4	7,3
c [mol/dm^3]	18,3·10^-3	9,2·10^-3
c [mol/dm^3]	14,4·10^-3	7,310^-3
c [mol/dm^3]	18,3·10^-5	9,2·10^-5
c [mol/dm^3]	14,217·10^-3	7,208·10^-3
c [mol/dm^3]	85,783·10^-3	92,792·10^-3
K	905,6	844,3

---