Na wiązkę elektronów w polu elektrycznym przechodzących przez obszar, w którym istnieje pole magnetyczne o indukcji B działa siła:
![]()
Siła ta skierowana prostopadle do kierunku wektora prędkości ![]()
i do wektora indukcji magnetycznej ![]()
.
W najprostszym przypadku ruch naładowanej cząstki odbywa się wzdłuż linii indukcji pola magnetycznego, przy takim ruchu cząstki kąt α zawarty między wektorem jej prędkości ![]()
i wektorem indukcji ![]()
równa się zero lub π, w wyniku czego siła Lorentza jest równa zero. Zatem na cząstkę nie działa pole magnetyczne.
W drugim przypadku rozpatrzmy ruch cząstki prostopadle do linii indukcji magnetycznej. W tym przypadku α=π/2 i siła Lorentza ma wartość ![]()
oraz skierowana jest prostopadle do wektorów ![]()
i ![]()
.
Cząstka zatem porusza się w płaszczyźnie prostopadłej do wektora indukcji magnetycznej, a siła Lorentza pełni rolę siły dośrodkowej:
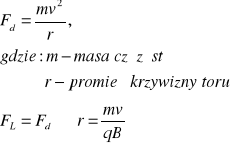
Z założenia pole jest jednorodne więc B=const., naładowana cząstka będzie się poruszać po okręgu, którego płaszczyzna jest prostopadła do pola magnetycznego. Kierunek obiegu cząstki zależy od znaku ładunku q cząstki:
![]()
w trzecim przypadku rozpatrzmy ruch naładowanej cząstki w polu magnetycznym gdy jej wektor ![]()
skierowany jest pod dowolnym kątem αdo wektora indukcji ![]()
. Rozłóżmy wektor v na dwie skłaowe:
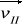
- składowa równoległa do wektora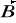
.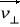
- składowa prostopadła do wektora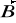
.
Prędkość ![]()
nie ulega zmianie w polu magnetycznym (patrz przypadek pierwszy). W wyniku posiadania przez cząstkę niezerowej składowej ![]()
cząstka powinna obiegać po okręgu, którego płaszczyzna jest prostopadła do wektora ![]()
, a promień ![]()
. Jak widzimy cząstka uczestniczy w dwóch ruchach jednocześnie w wyniku czego cząstka porusza się po linii śrubowej, której oś pokrywa się z linią indukcji pola magnetycznego, a skok wynosi
![]()
Pole elektryczne działa na cząstkę naładowaną z siłą ![]()
siła ta wytwarza przyspieszenie ![]()
. Rozważmy przypadek gdy do jednorodnego pola elektrycznego wprowadzamy cząstkę o masie m i ładunku q i puszczamy ją swobodnie. Ruch cząstki w tym polu jest podobny do ruchu ciała materialnego w ziemskim polu grawitacyjnym.
Rys.1. Ruch ładunku w polu elektrycznym
Stosujemy równanie ruchu jednostajnie przyspieszonego:
![]()
praca jaką wykonuje pole elektryczne o natężeniu E nad ładunkiem q na drodze ds. wynosi: ![]()
, ponieważ ![]()
. Jeśli różnica potencjałów wynosi U, to przy przesunięciu pola wykonuje pracę
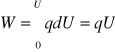
skutkiem działania pola jest wzrost prędkości cząstki do wartości ![]()
. Opisane zjawisko wykorzystuje się m.in. do wyznaczania ładunku właściwego elektronów. Podstawowym przyrządem służącym do tego celu jest lampa Browna. Elektrony wybiegające na wskutek termoemisji z katody lampy są poddawane działaniu pola elektrycznego pomiędzy katodą a anodą lampy.
Skutkiem działania pola elektrycznego jest wzrost prędkości elektronów od wartości v = 0 (przy katodzie), czyli energia elektryczna elektronu po dojściu do anody wynosi:
![]()
, czyli ![]()
Biegnący z taką prędkością elektron lub wiązka elektronów uderza w ekran lampy powodując pojawienie się plamki świetlnej. Plamka ta zostanie przesunięta o pewną wartość y, gdy wiązka elektronów przed uderzeniem w ekran przejdzie przez jednorodne pole magnetyczne. Natężenie pola magnetycznego wewnątrz cewek jest równe:

Znając wartość sił działających na wiązkę elektronów przechodzącą przez pole magnetyczne:
![]()
![]()
Wiedząc, że dla próżni B=μ0 H , ![]()
oraz ze wzoru [5]
wstawiając wartość prędkości v możemy napisać:
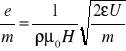
![]()
Promień krzywizny ruchu elektronów ![]()
wiąże się z wielkością odchylenia plamki y na ekranie lampy oraz z odległością l cewek odchylających od ekranu zależnością:
![]()
Podstawiając te wielkości ostatecznie otrzymamy:
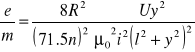
a po podstawieniu za R wartości związanych z układem pomiarowym stosowanym w laboratorium:
![]()
Wyszukiwarka