Wykonały: Szczecin 26.01.04 r.

Grażyna Graczyk

Anita Augustyniak

POLITECHNIKA SZCZECIŃSKA

ZAKŁAD CHEMII FIZYCZNEJ

Laboratorium studenckie

Sprawozdanie z wykonania ćwiczenia nr 9:

„Wyznaczanie ciepła parowania heksanu z pomiaru zależności prężności pary od temperatury.”

Wstęp:

W układzie dwufazowym ciecz-para cząsteczki w warstwie powierzchniowej lustra cieczy obdarzone do pokonania sił oddziaływania międzycząsteczkowego energią mogą opuścić ciecz przechodząc do wolnej przestrzeni nad powierzchnią gazową, wypełniającą pozostałą część zamkniętego naczynia. Intensywność tego procesu wzrasta ze wzrostem temperatury. W miarę wzrostu stężenia cząsteczek w fazie gazowej obserwuje się w coraz większym stopniu proces odwrotny, tj. przechodzenie pewnej ich liczby do fazy ciekłej. Jest to proces skraplania. W miarę upływu czasu szybkość parowania maleje, szybkość skraplania rośnie. Gdy szybkość parowania zrówna się z szybkością skraplania, ustali się stan równowagi dynamicznej. Równowagę tę charakteryzuje właściwa dla danej cieczy prężność pary nasyconej odpowiadająca danej temperaturze. Prężność pary nasyconej nie zależy od ilości substancji znajdującej się w poszczególnych fazach ani też od zajmowanych przez nią objętości. Jest ona głównie funkcją temperatury i stanowi miarę stężenia substancji w fazie gazowej. Przy ponownym ogrzaniu układu zamkniętego, rośnie temperatura i naruszony zostaje w nim stan równowagi. Wzrasta energia cząstek, rośnie szybkość parowania, maleje szybkość skraplania, wzrasta prężność pary nad roztworem. Ponownie ustala się stan równowagi na innym poziomie temperatury. Każdej temperaturze T odpowiada właściwa dla niej prężność pary nasyconej p. Gdy prężność pary nad cieczą w otwartym naczyniu stanie się równa ciśnieniu zewnętrznemu, wtedy parowanie zachodzi w całej masie cieczy, czyli ciecz wrze. Gdy ciśnienie zewnętrzne jest równe 1 Atm odpowiadająca mu temperatura nosi nazwę normalnej temperatury wrzenia. Krzywa będąca miejscem geometrycznym punktów, charakteryzujących stan równowagi między fazami ciekłą i gazową nosi nazwę krzywej parowania. Krzywa ta urywa się w punkcie krytycznym, gdzie zanika różnica między cieczą i parą, a powyżej istnieje tylko jedna faza.

Proces parowania wymaga dostarczenia do układu pewnej ilości energii na sposób ciepła, która w odniesieniu do 1 mola danej cieczy nosi nazwę molowego ciepła parowania H i jest zużywana na zwiększenie energii cząsteczek opuszczających ciecz (wewnętrzne ciepło parowania L_i ) oraz pracę A rozszerzenia układu od objętości molowej cieczy do objętości molowej pary przeciwko ciśnieniu zewnętrznemu p.

(1)

Molowe ciepło parowania jest sumą obydwu tych udziałów :

(2)

W dużym oddaleniu od punktu krytycznego V^(g)>> V^(c) i wzór drugi upraszcza się do postaci:

(3)

Ciepło parowania zmniejsza się ze wzrostem temperatury.

Proces parowania jest przemianą pierwszego rzędu (pierwszego rodzaju ) tj. taką, w której skokowo zmieniają się wartości pierwszych pochodnych potencjału termodynamicznego. Inne funkcje, np. entalpia molowa, entropia molowa, molowa energia wewnętrzna, molowa objętość i molowe ciepło właściwe w punkcie przemiany wykazują nieciągłość.

Relację między ciśnieniem równowagowym i temperaturą wyraża równanie Clausiussa-Clapeyrona:

(4)

Po scałkowaniu i zmianie logarytmów to równanie ma postać:

(5)

gdzie: H jest molowym ciepłem parowania cieczy.

Zestawienie danych uzyskanych w trakcie wykonywania doświadczenia

Ciśnienie atmosferyczne wynosi : p_atm. = 773 mm Hg.

T [C]	T [K]	1 / T =xi	h1 [mmHg]	h2 [mmHg]	h [mmHg]	p=patm -h	log p=yi	xiyi	xi^2
18,8	291,95	0,003425	689	83	606	167	2,222716	0,007613	1,17323E-05
22,9	296,05	0,003378	685	87	598	175	2,243038	0,007577	1,14096E-05
26,9	300,05	0,003333	682	91	591	182	2,260071	0,007532	1,11074E-05
29,8	302,95	0,003301	678	96	582	191	2,281033	0,007529	1,08958E-05
31,7	304,85	0,00328	670	107	563	210	2,322219	0,007618	1,07604E-05
35,5	308,65	0,00324	653	127	526	247	2,392697	0,007752	1,04971E-05
SUMA		0,019957					13,72178	0,045621	6,64025E-05

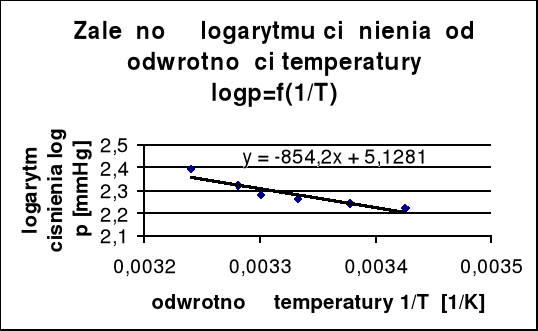
Obliczenie molowego ciepła parowania heksanu przy pomocy metody graficznej :

y = ax + b

gdzie:

Wybieramy dwa punkty z powyższego wykresu i przy pomocy ich współrzędnych położenia, korzystając z równania obliczamy współczynnik kierunkowy prostej :

współrzędne punktów : x₁ = 0,00325 ; y₁ = 2,352

x₂ = 0,00336 ; y₂ = 2,258

a = -854,545

[J/mol]=16,362 [KJ/mol]

Obliczenie współczynnika a metodą najmniejszych kwadratów :

Obliczenie molowego ciepła parowania heksanu przy pomocy metody najmniejszych kwadratów :

[J/mol] = 16,3554 [KJ/mol]

Wartość literaturowa dla ΔH_par=28850 [J/mol]=28,85 [KJ/mol]

Obliczenie odchylenia procentowego :

a). wartość wyznaczona metodą graficzną;

28,85 - 16,362 = 12.448

b). wartość wyznaczona metodą najmniejszych kwadratów:

28,85- 16,3554 = 12,4946

---