Rozwiązanie metodą superpozycji

Oznaczmy:

C - rzut prostokątny punktu A na odcinek OB

r = OA

l = AB

c = CB

y = AC

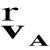
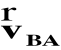
Wykorzystujemy twierdzenie mówiące, że prędkość w ruchu złożonym jest sumą wektorową prędkości unoszenia i prędkości względnej

Gdzie:

- wektor prędkości unoszenia (w tym przypadku wektor prędkości punktu A)

- wektor prędkości względnej (w tym przypadku wektor prędkości punktu B względem punktu A)

Ponadto wiemy, że

jest prostopadły do odcinka OA

jest prostopadły do odcinka AB, gdyż punkt B względem punktu A może wykonywać tylko ruch obrotowy

ma kierunek poziomy, gdyż prowadnice wodzika uniemożliwiają ruch w innych kierunkach

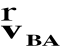
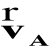
Sumujemy wektory:

Wiemy, że wartość wektora
wynosi

Ponadto wektor
tworzy z kierunkiem pionowym kąt α, gdyż jest prostopadły do odcinka OA, a odcinek OA tworzy kąt α z kierunkiem poziomym. Oznacza to, że kąt między wektorami
i
wynosi 90 - α.

Z kolei wektor
tworzy z kierunkiem pionowym kąt γ, gdyż jest prostopadły do odcinka AB, a odcinek AB tworzy kąt γ z kierunkiem poziomym. Oznacza to, że kąt między wektorami
i
wynosi 90 - γ. Kąt pomiędzy wektorami
i
będzie więc wynosił 180 - (90 - α) - (90 - γ) = 180 - 90 + α - 90 + γ = α + γ

Możemy więc zapisać, że:

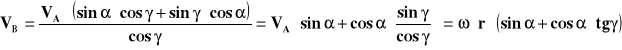
Do wyznaczenia pozostaje więc tangens kąta γ

=

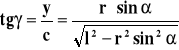
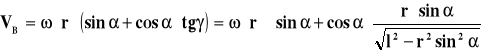
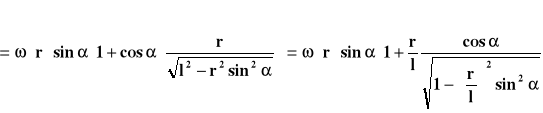
C