PD do Cw.2 z 24.02.2010

Zad.1

Sprawdzić czy spełniony jest warunek konieczny zbieżności szeregu.

Wyznaczyć ciąg sum częściowych i rozstrzygnąć z definicji czy szereg jest zbieżny i jaką ma sumę

odp.szereg zbieżny suma równa się

Zad.2

Korzystając z własności szeregu geometrycznego obliczyć sumę
. Odp

Zad.3

Z kryterium porównawczego zbadać zbieżność szeregów

a)
, b)
, c)

a) rozbieżny, b) zbieżny, c) zbieżny.

Zad.4

Z kryterium ilorazowego lub pierwiastkowego zbadać zbieżność szeregów

a)
, b)
, c)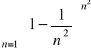

a) zbieżny, b) zbieżny, c) rozbieżny.

To jest praca minimum. Reszta zadań do samodzielnej pracy w zbiorach

Banaś J, Wędrychowicz S., Zbiór zadań z analizy matematycznej, rozdz.XV

Krysicki W, Włodarski L., Analiza matematyczna w zadaniach cz.I rozdz.III

---