Drgania nietłumione układu o jednym stopniu swobody wymuszone siłą harmonicznie zmienną

Równanie ruchu

stąd równanie różniczkowe drgań wymuszonych nietłumionych

Częstość kołowa drgań własnych masy
,

Rozwiązanie równania jest równe sumie rozwiązania ogólnego równania jednorodnego oraz rozwiązania szczególnego.

gdzie

Po podstawieniu wyrażenia x₁ do równania ruchu otrzymamy

wartość amplitudy drgań wymuszonych A

stąd

Zatem poszukiwanym rozwiązaniem szczególnym będzie

Rozwiązanie równania ruchu jest

Po podstawieniu warunków początkowych
otrzymamy wartości stałych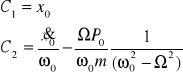

Podstawiając stałe do rozwiązania równania drgań wymuszonych otrzymujemy

Pierwsze dwa wyrazy przedstawiają drgania własne układu, wynikające z przyjętych warunków początkowych.

Wyraz trzeci przedstawia drgania o częstości własnej zależne od amplitudy i częstości własnej. Wyraz czwarty przedstawia drgania wymuszone o częstości siły wymuszającej.

WSPÓŁCZYNNIKI AMPLIFIKACJI (wzmocnienia amplitudy) - odniesione do przemieszczenia statycznego masy pod wpływem siły P₀

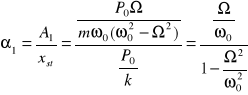
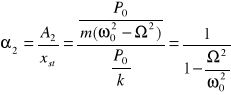
Wykresy zależności współczynników amplifikacji

(wzmocnienia amplitudy) funkcji ilorazu częstości drgań.

REZONANS

Rezonans w układach zachowawczych (bez tłumienia) o drganiach wymuszonych harmonicznie

Rezonans wystąpi wtedy gdy częstość kątowa drgań własnych równa jest częstości wymuszenia
zatem równanie ruchu drgajacego
gdzie
,

Rozwiązanie równania ruchu jest następujące (przy uwzględnieniu wartości początkowej)

jeśli
to zgodnioe z regułą de l'Hospitala zastępujemy licznik i mianownik ich pochodnymi względem Ω i obliczamy granicę przy

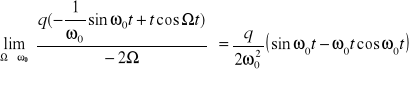
zatem rozwiązanie

Współrzędna x punktu drgającego wzrasta nieograniczenie z czasem co do wartości bezwzględnej co pokazano na rysunku

x

k

m

P(t)

x(t)

t