Konrad Dróżka Jean-Paul Armache

Ćwiczenie numer 105

Temat:

WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ STATYCZNĄ

Ocena:

Wyznaczanie modułu sztywności metodą statyczną.

1.Metoda pomiaru.

Prawo Hook'a dla odkształceń postaciowych wyraża się wzorem:

p = G tg γ

gdzie p to ciśnienie styczne do powierzchni, G - to moduł sztywności(sprężystości postaciowej) . Dla małych kątów(a o takie tutaj występują) możemy przyjąć że, tg γ ≈ γ.

Rysunek przedstawia odkształcenie postaciowe.

Prawu Hook'a podlega również pręt skręcany o niewielki kąt ϕ zewnętrznym momentem siły M, gdyż można go podzielić na analogiczne elementy.

M = D ϕ

Gdzie D jest to moment kierujący pręta o promieniu R i długości l wyrażony wzorem:

π • G •R ⁴

D = —————

2l

W ćwiczeniu używamy pręta w celu wyliczenia G. Jeden koniec pręta umieszczamy w nieruchomych widłach a drugi obciążamy ciężarem i•m•g gdzie k jest to liczba ciężarków o średniej masie m. Działamy wtedy momentem siły M równym:

M = i • m • g • r

Gdzie r to ramie siły skręcającej.

Przyrost kąta ϕ powinien być wprost proporcjonalny d masy ciężarków, a więc:

ϕ = a • i • m

dane doświadczalne pozwolą metodą najmniejszych kwadratów wyliczyć współczynnik a. Wzór na moduł sztywności otrzymujemy po porównaniu wzorów na M i G przy uwzględnieniu wzoru na D (pominięto tutaj liczbę ciężarków a masa będzie masą łączną wszystkich ciężarków).

2 l • g • r M 2 l • g • r 1

G = ———— • —— = ——— • — (1)

π•R ⁴ ϕ π•R ⁴ a

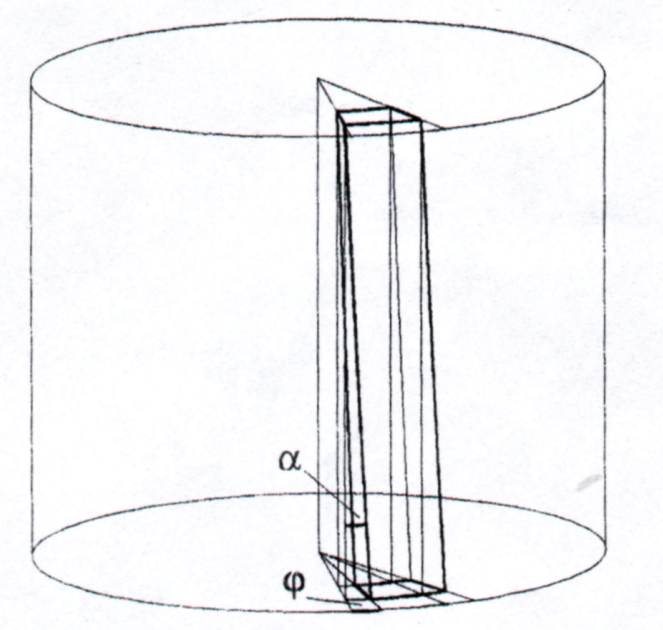
Istnieje różnica pomiędzy kątem skręcania drutu ϕ a kątem skręcania walca α (rysunek powyżej). Ponieważ oba te kąty oparte są na tym samym łuku zakreślonym przez dowolny punkt materialny możemy zapisać wzór, który je łączy:

α = (R / L) • ϕ

2.Tabele z wartościami wielkości mierzonych.

Masy ciężarków uzyskane za pomocą wagi technicznej:

Ciężarek 1	Ciężarek 2	Ciężarek 3	Ciężarek 4	Ciężarek 5	Ciężarek 6	Średnia masa
1003	1007,2	1015,2	1010,7	1004	1012	1008,68

Istnieje możliwość różnicy w promieniach na różnych odcinkach prętów więc mierzymy średnicę w 5 różnych miejscach:

TABELE DLA MATERIAŁU 1.

L.p.	1		2		3		4		5		Rśr	Błędy pomiaru
2R i [mm]	11	12		11		10		11,5		11,1		Średnicy [mm]	2 mm
R i [mm]	5,5	6		5,5		5		5,75		5,55		Promienia[mm]	1 mm

Długość pręta wynosi: l = 99,5 cm ± 1 cm

Średnica tarczy wynosi: 2r = 10,5 cm ± 0,2 cm

Tabela przedstawiająca zmiany kątów podczas obciążania kolejnymi ciężarkami(i - kolejna liczba ciężarków):

Liczba ciężarków	0	1	2	3	4	5	6	7
m i	0	1008,5	2017	3025,5	4034	5042,5	6051	7059,5
ϕ i [°]	0,1	1,1	2	3,4	4,3	5,4	6,3	7,1
ϕ i [rad]	0,0055 π	0,0061 π	0,0111 π	0,1888 π	0,0238 π	0,3 π	0,035 π	0,0394 π

y = 1,47968 e-5 x

TABELE DLA MATERIAŁU 2.

L.p.	1		2		3		4		5		Rśr	Błędy pomiaru
2R i [mm]	10	10,3		9,5		10,5		9,7		10		Średnicy [mm]	2 mm
R i [mm]	5	5,15		4,75		5,25		4,85		5		Promienia[mm]	1 mm

Długość pręta wynosi: l = 99,5 cm ± 1 cm

Średnica tarczy wynosi: 2r = 10,4 cm ± 0,2 cm

Liczba ciężarków	0	1	2	3	4	5	6	7
M. i	0	1008,5	2017	3025,5	4034	5042,5	6051	7059,5
ϕ i [°]	0	0,4	0,7	1	1,4	1,9	2,2	2,4
ϕ i [rad]	0 π	0,0022 π	0,0038 π	0,0055 π	0,0077 π	0,0105 π	0,0012 π	0,0133 π

y = 1,93522 e-6 x

TABELE DLA MATERIAŁU 3.

L.p.	1		2		3		4		5		Rśr	Błędy pomiaru
2R i [mm]	10,2	9,7		10,4		9,6		10,1		10		Średnicy [mm]	2 mm
R i [mm]	5,1	4,85		5,2		4,8		5,05		5		Promienia[mm]	1 mm

Długość pręta wynosi: l = 99,5 cm ± 1 cm

Średnica tarczy wynosi: 2r = 10,3 cm ± 0,2 cm

Liczba ciężarków	0	1	2	3	4	5	6
M. i	0	1008,5	2017	3025,5	4034	5042,5	6051
ϕ i [°]	0	1	2,2	3,4	4,6	5,7	6,9
ϕ i [rad]	0 π	0,0055 π	0,0122 π	0,0188 π	0,0255 π	0,0316 π	0,0383 π

y = 6,38855 e-6 x

3.Wykres przedstawiający zależność ϕ od m.

Wykres znajduje się na dołączonej kartce.

4.Obliczanie wartości modułu sztywności dla każdego materiału.

Obliczyliśmy współczynnik a używając metody najmniejszych kwadratów i średni błąd ich pomiaru.

Materiał 1: 4,7099 • e-3 [kg] ∆a = 0,0005 • e-2 [g]

Materiał 2: 6,1599 • e-4 [kg] ∆a = 0,0005 • e-3 [g]

Materiał 3: 2,0176 • e-3 [kg] ∆a = 0,0005 • e-3 [g]

Teraz korzystając ze wzoru na moduł sztywności (wzór 1) otrzymujemy:

dla materiału 1: G = 7,3 • e 7 [kg/m • s]

dla materiału 2: G = 8,4 • e 11 [kg/m • s]

dla materiału 3: G = 2,6 • e 11 [kg/m • s]

5.Rachunek błędów.

Błąd bezwzględny można obliczyć ze wzoru:

∆l ∆r 4∆R ∆a

∆G = G_obl • — • — • — • —

l r R a

6.Wynik końcowy.

Po obliczeniu błędu dla każdego materiału wynik końcowy możemy zapisać w postaci:

G = G_obl ± ∆G

A więc:

Materiał 1: G = 7,3 • e 7 [kg/m • s] ± 0,7 e 7 [kg/m • s]

Materiał 2: G = 8,4 • e 11 [kg/m • s] ± 0,9 • e 11 [kg/m • s]

Materiał 3: G = 2,6 • e 11 [kg/m • s] ± 0,3 • e 11 [kg/m • s]

7.Dyskusja na temat czynników powodujących błędy.

Głównym źródłem błędów jest niedokładność przy mierzeniu długości pręta. Wynika to w głównej mierze z tego , że nie było możliwości przyłożenia linijki do pręta gdyż przy jego końcu była tarcza z noniuszem. Kolejną przyczyną błędu może być utrudnione odczytywanie informacji z noniusza.

---