AKADEMIA GÓRNICZO - HUTNICZA W KRAKOWIE			Grupa B Rafał Szemraj
EAIiE	2001/2002		Rok II Semestr IV	Elektrotechnika		Rok B Grupa 8
Temat: Analiza podstawowych układów dyskretnych.
Data wykonania: 2002-04-29		Data zaliczenia:			Ocena:

1. Wstęp teoretyczny:

Dyskretyzację sygnałów ciągłych (próbkowanie tychże sygnałów w określonych przedziałach czasu) przeprowadza się przede wszystkim w celu umożliwienia analizy i badania przebiegów za pomocą urządzeń cyfrowych, które charakteryzują się względnie dużą dokładnością obliczeń a, przede wszystkim, bardzo dużą szybkością działania. Aby np. komputer (który wykonuje operacje na sygnałach binarnych) mógł przetworzyć określone dane muszą być one przekazane mu w formie cyfrowej. Dlatego też na wejście takiego urządzenia cyfrowego nie podaje się sygnału ciągłego w czasie, lecz odpowiednie jego wartości odczytane co pewien (z góry określony) przedział czasu. Taką operację nazywamy właśnie przekształcaniem dyskretnym.

W teoretycznych rozważaniach na temat sygnałów dyskretnych zastosowanie znalazło przekształcenie z, będące odpowiednikiem przekształcenia Laplace'a dla układów ciągłych.

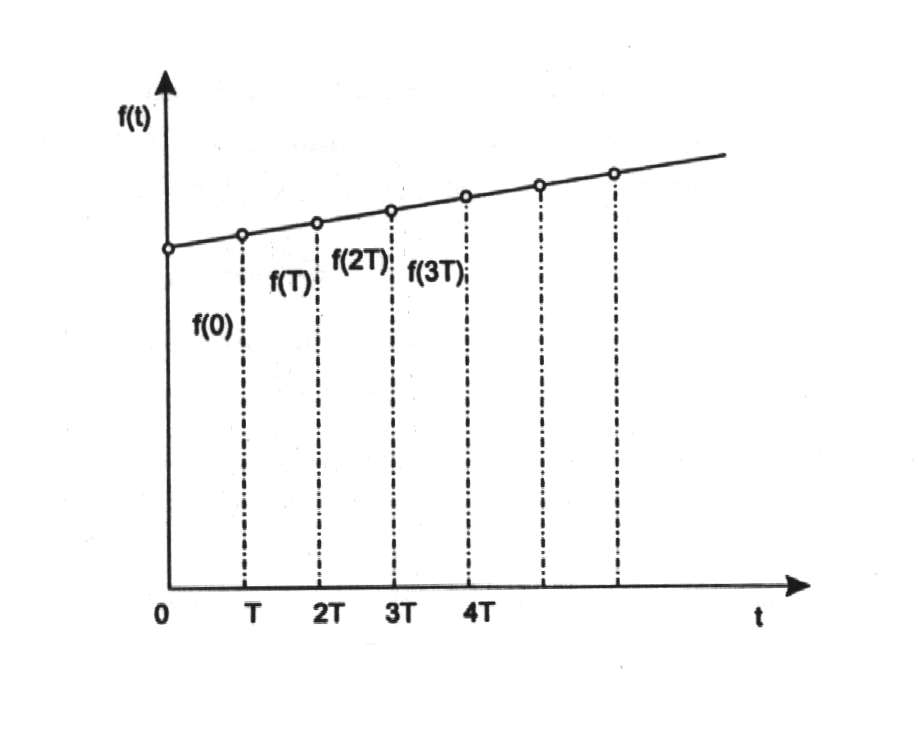
Rys1. Dyskretyzacja sygnału z okresem próbkowania T.

W układach dyskretnych nie analizuje się sygnału w całej dziedzinie czasu, ale uwagę poświęca się jedynie odpowiednim jego wartościom odczytywanym dla określonych wartości czasu. Wartości te „czytane” są dla
, gdzie T jest ustaloną liczbą dodatnią, nazywaną okresem próbkowania. Wtedy dla
mamy odpowiadające im wartości sygnału dla danej chwili czasu:
. Mając te wartości korzystając z przekształcenia z możemy przyporządkować danej funkcji f(t) funkcję zmiennej zespolonej z korzystając ze wzoru:

Gdy dokładnie przyjrzymy się temu wzorowi to zauważymy, z ma on formę szeregu potęgowego dla którego zachodzi zależność
, gdzie
jest promieniem zbieżności tego szeregu. F(z) jest transformatą funkcji f(t). Jeżeli funkcja f(t) jest nieciągła w punkcie nT, to zakładamy że:

i że ta granica istnieje dla każdego n.

Dla przekształcenia z występuje kilka własności. Oto parę z nich:

• Twierdzenie o wartości początkowej:
  

• Twierdzenie o wartości końcowej:
  

• Twierdzenie o zmianie skali na płaszczyźnie zmiennej zespolonej:

Jeśli
to

• Przekształcenie z jest przekształceniem liniowym.

Przykłady transformat najczęściej spotykanych przebiegów.

1. Transformata skoku jednostkowego:

Skok jednostkowy ma wartość równą 1 dla
tzn.

Zgodnie ze wzorem na przekształcenie z otrzymujemy:

Mamy więc szereg geometryczny o wyrazie początkowym równym 1 i
, a zgodnie ze wzorem na sumę wyrazów szeregu geometrycznego otrzymujemy transformatę z skoku jednostkowego w postaci wielomianu:

2. Transformata funkcji
   :
   

3. Transformata funkcji
   :
   

4. Transformata funkcji
   :
   

Transmitancja dyskretna i jej postacie:

Definicja: „Transmitancją dyskretną danego członu nazywamy stosunek dyskretnego sygnału wyjścia danego członu do dyskretnego sygnału podawanego na wejście danego obiektu.”

Postać dyskretna zero - biegunowa (DZP) transmitancji:

Dla tej postaci widoczne są bieguny i miejsca zerowe transmitancji co pozwala na szybką ocenę zachowania się danego układu i jego stabilności.

Postać dyskretna wymierna (DTF) transmitancji:

Postać ogólna transmitancji. Z takiej postaci łatwo przejść do postaci ułamków prostych a w dalszej kolejności do postaci funkcji w dziedzinie czasu (odwrotna przekształcenie z).

2. Badanie członu opóźniającego o transmitancji dyskretnej (Unit Delay):

Budowę powyższego schematu (tak jak zresztą pozostałych) oraz badanie jego działania przeprowadzono w SIMULINKU będącego integralną częścią programu MATLAB.

Powyższy schemat przedstawia sposób badania członu o transmitancji dyskretnej
(Unit Delay), który opóźnia sygnał wyjściowy w stosunku do wejściowego o jednostkę czasu. Kształ t przebiegu wyjściowego zależy od tego jak się ma stała próbkowania T do okresu „przesuwanego przebiegu”. Na poniższych wykresach pokazano przebieg sygnału wejściowego o okresie 2s, szerokości impulsu 1s i wysokości impulsu 1,5. Stała próbkowania wynosiła T = 1s.

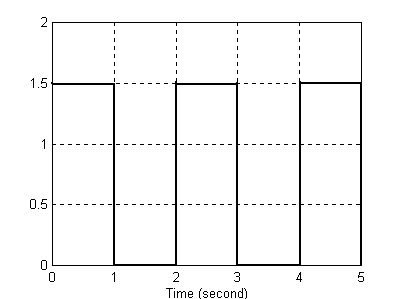
Sygnał wejściowy z generatora impulsów prostokątnych.

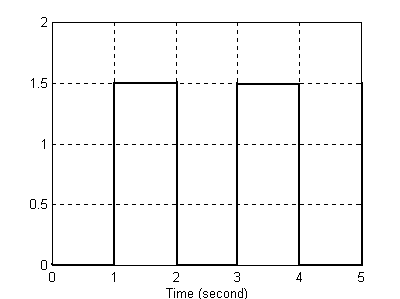
Sygnał wyjściowy z obiektu Unit Delay.

Widzimy, że sygnał został dokładnie opóźniony o 1 sekundę (przy czym kształt sygnału pozostał niezmieniony). Urządzenie „odczytało” wartość sygnału dla t = 0 i przesunęło go 0 1 s w prawo (opóźniło), po czym ta sama operacja została wykonana na sygnale wejściowym dla t = 1s,2s,3s,4s ...

W każdej chwili próbkowania czytana jest inna wartość niż chwilę przed - dzięki temu kształt przebiegu wyjściowego jest taki sam jak kształt wejścia.

Zobaczmy co się stanie gdy ten sam przebieg będziemy próbkowali ze stałą równą T = 2.

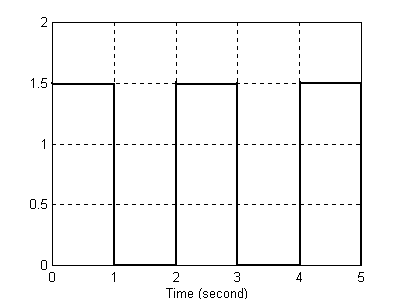
Wejście

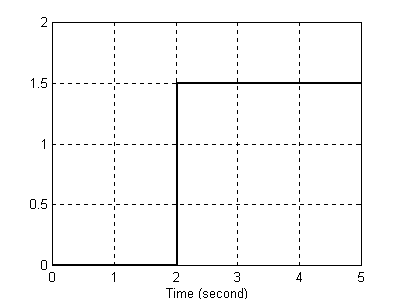
Wyjście

Widzimy, że teraz kształt sygnału wyjściowego jest całkiem inny niż sygnału wejściowego. Spróbujmy się przyjrzeć dlaczego: Obiekt próbkuje sygnał w chwili t = 0 i odczytuje wartość f(t) = 1,5 opóźniając ją zarazem o 2s (tyle ile wynosi stała T próbkowania w tym przypadku). Stąd mamy dla przebiegu wyjściowego f(t) = 0 dla t∈[0,2) i f(t) = 1,5 dla t∈[2,4). W następnym kroku zostaje spróbkowany sygnał wejściowy dla t = 2s czyli f(t) = 1,5. Tak samo będzie dla t = 4s, 6s, 8s, itp. Obiekt co 2 sekundy będzie od tego momentu próbkował tę samą wartość więc przesunięcie (opóźnienie) nie jest widoczne - sygnał od t = 2s ma tę samą wartość ( f(t) = 1,5 dla t ≥ 2. Dla takich nastawień układu sygnał wyjściowy ma postać skoku jednostkowego o amplitudzie równej amplitudzie sygnału wejściowego.

WNIOSEK: Dla powyższego układu dobór stałej próbkowania mniejszej lub równej okresowi przebiegu wejściowego powoduje dokładne odtworzenie kształtu sygnału wejściowego na wyjściu. Przy stałych większych niż okres układ „nie nadąża” za zmianami sygnału wejścia i, co za tym idzie, kształty sygnału wejściowego i wyjściowego są różne.

3. Badanie członu opisanego dyskretną transmitancją czynnikową (zero - biegunową).

W tym punkcie badaliśmy człon o transmitancji dyskretnej przedstawionej w ten sposób, że od razu widoczne są zera i bieguny danej transmitancji. Wykresy przedstawiają kształt sygnału wymuszenia (skok jednostkowy

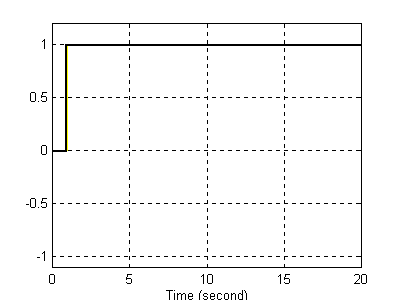
Wejście (skok jednostkowy).

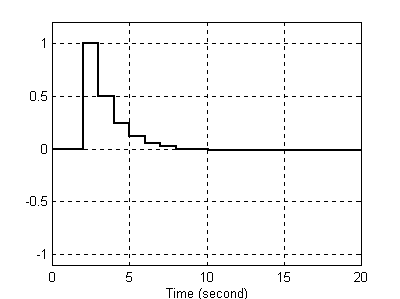
Sygnał wyjściowy

Kształt sygnału wyjściowego w dużej mierze zależy od wyrażenia znajdującego się w mianowniku w nawiasie (od jednego z biegunów transmitancji). Warto zauważyć, że gdy tym biegunem jest z = 1, to układ spełnia rolę członu opóźniającego jednostkowego (otrzymalibyśmy na wyjściu sygnał wejściowy opóźniony o jedną sekundę. W tym przypadku (dla bieguna z = 0,5) układ zachowuje się jak układ różniczkujący rzeczywisty z inercją. Sygnał też jest przesunięty o 1s (wpływ zerowego bieguna transmitancji). Opóźnienie (inercja) układu zależy od wartości wspomnianego bieguna (im biegun bliższy jest zeru np.: z = 0,1 tym różniczkowania przebiega szybciej; im biegun bliższy jedynki tym sygnał wolniej dąży do ustalenia.

4. Badanie odpowiedzi członu dyskretnego Discrete Transfer Fcn na wymuszenie skokiem jednostkowym.

Na wejście układu znowu podajemy skok jednostkowy. Wartość w liczniku transmitancji odpowiada jedynie za wzmocnienie układu. Przyjrzyjmy się odpowiedzi układu na skok jednostkowy:

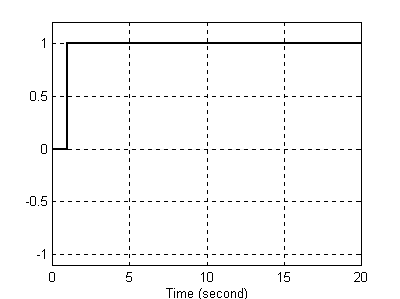
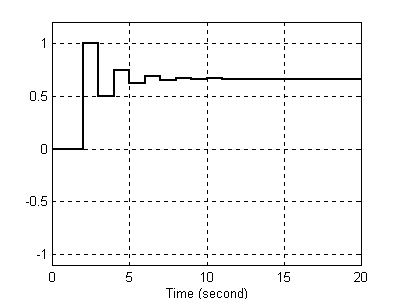
Postać sygnału wyjściowego.

Jak już wspomniałem od liczby w liczniku zależy jedynie wzmocnienie. Natomiast od wartości biegunów zależy kształt przebiegu wyjściowego. Dla z = -0,5 (na rysunku) widzimy powoli zanikające oscylacje i ustalenie się przebiegu. Dla bieguna równego z = -1 przebieg ma kształt oscylacji o stałej amplitudzie. Dla z < -1 oscylacje te są coraz większe (odpowiedź niestabilna). Inaczej jest dla dodatnich biegunów - dla wartości z∈(0,1) przebieg ulega całkowaniu (im biegun bardziej zbliżony do 1 tym całkowanie jest bardziej „łagodniejsze” i odpowiedź stabilizuje się. Dla z = 1 (typowy integrator) i z > 1 sygnał wejściowy jest całkowany bez ustalania się odpowiedzi.

5. Badanie działania dyskretnego członu całkującego Discrete-Time Integrator.

Badanie członu dyskretnego całkującego polegało na zbadaniu jego odpowiedzi na wymuszenie sygnałem impulsowym prostokątnym w zależności od różnych wartości stałej całkowania T. Poniższy rysunek pokazuje odpowiedź układu ze stałą T = 1.

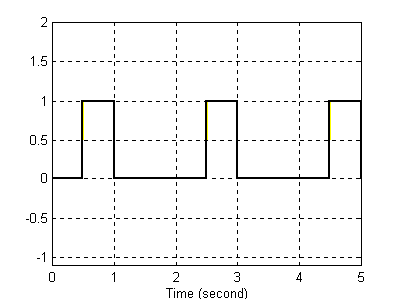
Sygnał wejściowy

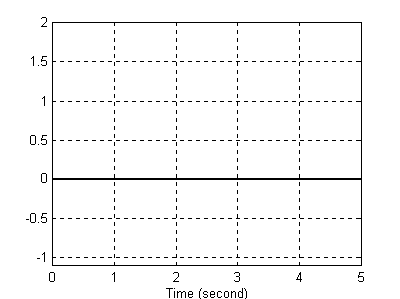
Odpowiedź integratora ze stałą T =1s.

Jak widać odpowiedzią na zadane wymuszenie integratora tego typu jest zerowa odpowiedź. Wynika to z tego, że dla t = 1s, 2s, 3s, 4s ..., a więc dla tych momentów w których integrator próbkuje sygnał wartość sygnału jest równa zero. Popatrzmy na odpowiedź na takie samo wymuszenie integratora ze stałą T = 0,1s

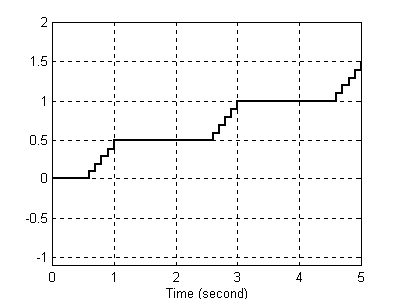
Odpowiedź integratora ze stałą T = 0,1s.

Jak zauważamy tu całkowanie odbywa się poprawnie. Dla pierwszych 0,5s nic się nie dzieje (wartość sygnału wejściowego w tym przedziale jest równa zero). Począwszy od 0,5s (skok sygnału wejściowego do wartości 1) następuje całkowanie sygnału wejścia co 0,1s (wartość stałej). Trwa to do zaniku impulsu na wejściu (co następuje dla chwili t = 1s). Widzimy, że integrator w tym momencie na swoim wyjściu utrzymuje sygnał na poziomie 0,5 (co odpowiada całce pojedynczego impulsu wejścia - polu pod impulsem 0,5*1 = 0,5). W momencie pojawienia się następnego impulsu następuje całkowanie do następnego poziomu (równego polu pod dwoma impulsami) itd. Dla wartości stałej z przedziału T∈(0,1) całkowanie odbywa się z dokładnością odwrotnie proporcjonalną do wartości tej stałej - im mniejsza stała, tym całkowanie odbywa się w małych odcinkach czasu i jest bardziej dokładniejsze.

6. Wnioski:

Jak widzimy w układach dyskretnych sama postać transmitancji nie daje nam ostatecznej informacji na temat kształtu odpowiedzi na dane wymuszenie. Duże znaczenie w każdym z powyższych układów ma stała próbkowania, której wartość znacznie wpływa na działanie poszczególnych członów. Dzięki zawartym w bibliotekach Simulinka elementom możliwe jest szybkie „skonstruowanie” interesującego nas układu i dokładna jego analiza.

	AKADEMIA GÓRNICZO - HUTNICZA W KRAKOWIE			Grupa B Rafał Szemraj
EAIiE	2001/2002		Rok II Semestr IV	Elektrotechnika		Rok B Grupa 8
Temat: Układ z ciągłym regulatorem cyfrowym.
Data wykonania: 2002-05-02		Data zaliczenia:			Ocena:

1. Badanie symulacyjne układu ciągłego z regulatorem cyfrowym.

Głównym celem ćwiczenia jest dobór regulatora cyfrowego w obwodzie elementu ciągłego według dwóch następujących kryteriów:

• Minimalny czas regulacji
  

• Zerowy uchyb regulacji
  

Na wejście powyższego układu podawany jest sygnał skoku jednostkowego
zatem sygnał wejściowy dyskretny ma postać:
, czyli
po zastosowaniu przekształcenia z. Występujący w układzie obiekt o transmitancji
to tzw. ekstrapolator zerowego rzędu (0-holder), który opóźnia sygnał i całkuje go. Obiekt umieszczony ze ekstrapolatorem to element ciągły o transmitancji
.

Aby wyznaczyć transmitancję dyskretną kaskadowego połączenia ekstrapolatora i obiektu regulacji należy najpierw przejść z dziedziny zespolonej s do dziedziny czasu (odwrotne przekształcenie Laplace'a) a potem zastosować na funkcji czasu przekształcenie z, czyli:

Wykonując działania po kolei mamy:

Po rozłożeniu pierwszego czynnika w nawiasie na ułamki proste mamy:

. Mamy więc teraz:

. Stosując odwrotne przekształcenie Laplace'a otrzymujemy:

Transformata Z powyższej funkcji ma postać:

Po podstawieniu za T_i = 1 i po wymnożeniu mamy postać transmitancji zastępczej dyskretnej obiektu:

Transmitancja dyskretna całego układu (z pętlą ujemnego sprzężenia zwrotnego) wynosi:

, gdzie
jest transmitancją dyskretną regulatora cyfrowego, której postaci teraz szukamy.

Przyjmując oznaczenia:
i
mamy:

Patrząc na postać transmitancji obiektu widzimy że jest on 2-go rzędu. Aby zapewnić minimalny i skończony czas regulacji musimy spełnić warunek:

Teraz zajmiemy się spełnieniem drugiego warunku, a więc zminimalizowaniem do zera uchybu dyskretnego:

Transm. uchybowa:

Zgodnie z twierdzeniem o wartości końcowej:

(warunek dla odchyłki ustalonej równej zero). Granica ta będzie równa zero jeżeli w liczniku transmitancji uchybowej pojawi się wyrażenie
. Stąd, przewidując postacie transmitancji:

i
mamy:

, a stąd:

Korzystając z wyliczonych współczynników i ze wzoru na transmitancję układu zamkniętego otrzymujemy, że:

2. Obserwacja graficzna działania układu z regulatorem o znalezionej transmitancji

Korzystając z bibliotek Simulinka poddano symulacji układ jak na rysunku poniżej:

Oto przebiegi jakie otrzymano:

Wejście (sygnał jednostkowy)

Odpowiedź układu z regulatorem na skok jednostkowy.

Jak widzimy zaprojektowany układ z regulatorem spełnia zadane na początku warunki - uchyb po ustaleniu się sygnału wynosi zero ( amplituda wyjścia i wejścia są równe ) a czas ustalania się odpowiedzi jest też względnie mały i wynosi 2s. Warte zauważenia jest brak oscylacji i przeregulowań w sygnale wyjściowym. Podany przykład szukania transmitancji regulatora jest przykładem na zastosowanie teorii sterowania w przypadkach układów, które mają za zadanie spełniać określone warunki. Znając te warunki a także posiadając odpowiednie wiadomości możemy znaleźć interesujące nas rozwiązanie a potem, np.: za pomocą Simulinka, sprawdzić jego działa

12

Obiekt

Ekstrapolator

ε^*(t)

Regulator

cyfrowy

ε(t)

Y(t)

X_Z(t)

_

H(s)

RC

G(s)

T_i

T_i

U^*(t)

y(nT_i)

---