WYTRZYMAŁOŚĆ MATERIAŁÓW (semestr II)

Podstawowe pojęcia i definicje

1. Określ główne zadania wytrzymałości materiałów.

• Zapewnienie bezpieczeństwa pracy elementów konstrukcyjnych poprzez sprawdzenie warunku wytrzymałościowego (określenie sił wewnętrznych)

• określenie stopnia odkształcenia rozpatrywanego elementu konstrukcyjnego, który stanowi miarę sztywności układu

• ustalenie, czy dwa poprzednie warunki mogą być równocześnie spełnione przy zastosowaniu mniejszych wymiarów elementów konstrukcyjnych (jest to związane z optymalizacją wykonania konstrukcji ze względu na jej ciężar własny i koszty zastosowanych elementów)

2. Zdefiniuj siłę skupioną oraz siłę ciągłą liniową, powierzchniową i objętościową

siły objętościowe - obciążenie odnoszące się do jednostki objętości ciała

siły powierzchniowe - obciążenie rozłożone jest na zadanej powierzchni ciała

siła skupiona - obciążenie, które działa na powierzchni bardzo małej w porównaniu z wymiarami rozpatrywanego elementu

siła ciągła liniowa - obciążenie rozłożone wzdłuż zadanej linii geometrycznej. Jego miarą jest iloraz przyłożonej siły do jednostki długości linii.

3. Podaj definicję układu statycznie wyznaczalnego.

Układ statycznie wyznaczalny (izostatyczny) jest to taki układ, w którym liczba niewiadomych statycznych (liczba reakcji) jest równa liczbie możliwych do ułożenia, niezależnych liniowo, równań równowagi, zapisanych w postaci analitycznej. S_N=0 (z układu równań równowagi można jednoznacznie określić wszystkie niewiadome statyczne)

4. Jaka jest różnica pomiędzy płytą, powłoką a tarczą.

tarcza - cienki krążek, którego obciążenie stanowią działające w jego płaszczyźnie promieniowe i osiowosymetryczne siły masowe oraz siły powierzchniowe na wewnętrznej i zewnętrznej powierzchni

powłoka - cienkościenny ustrój, którego jeden wymiar (grubość) jest mały w porównaniu z pozostałymi i którego powierzchnie skrajne są zakrzywione

płyta - cienkościenny ustrój, którego jeden wymiar (grubość) jest mały w porównaniu z pozostałymi i którego powierzchnia środkowa jest płaszczyzną

5. Podaj definicję materiału izotropowego i materiału jednorodnego.

jednorodny - żaden punkt nie jest wyróżniony

izotropowy - wykazujące jednakowe właściwości mechaniczne, niezależnie od kierunku działania sił

6. Na czym polega zasada myślowego przekroju?

Zasada polega na myślowym przecięciu ciała w rozpatrywanym miejscu. W celu określenia sił wewnętrznych odrzucamy jedną część przeciętego ciała, a następnie rozpatrujemy warunki równowagi pozostałej części. Po uwzględnieniu działających na nią sił zewnętrznych czynnych i biernych, siły wewnętrzne występujące w przekroju elementu mają charakter sił zewnętrznych.

7. Podaj definicję wektora głównego i momentu głównego układu sił.

Wektory:
zaczepione w punkcie A nazywamy wektorem głównym i momentem głównym układu sił (P₁...P_n) względem punktu A. Punkt A nazywamy środkiem redukcji.

8. Podaj definicję sił przekrojowych: siły poprzecznej, siły podłużnej i momentu zginającego, momentu skręcającego

siłą poprzeczną (tnącą) T w danym przekroju belki, nazywamy sumę składowych stycznych do przekroju, wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem

siłą podłużną (normalną) N w danym przekroju belki, nazywamy sumę składowych normalnych do przekroju, wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem

moment zginający (gnący) M_g w danym przekroju belki, nazywamy sumę momentów od wszystkich sił zewnętrznych, działających na część belki odciętą tym przekrojem

moment skręcający w danym przekroju poprzecznym pręta jest sumą algebraiczną momentów wszystkich par sił zewnętrznych, działających po jednej stronie tego przekroju i leżących w płaszczyznach prostopadłych do osi pręta

9. Podaj definicję naprężenia średniego i naprężenia w punkcie.

średnie wypadkowe naprężenie - wektor współ kierunkowy z działającą siłą ∆W na elementarne pole ∆A o wartości p_śr=∆W/∆A

naprężenie w punkcie - wektor współ kierunkowy z działającą siłą ∆W na elementarne pole ∆A→0 o wartości

10. Podaj definicję naprężenia normalnego i stycznego w punkcie.

naprężenia normalne - składowa wypadkowego naprężenia prostopadła do przekroju

naprężenia styczne - składowa działająca w płaszczyźnie przekroju

definiowanie naprężenia jako wektora w danym punkcie ciała jest dopuszczalne tylko wtedy, gdy myślowy przekrój traktujemy jako stały

11. Podaj zasadę de Saint-Venanta.

Jeżeli na niewielki obszar ciała działają kolejno statycznie równoważne obciążenia, to w odległości przewyższającej jego wymiary liniowe powstają praktycznie jednakowe stany naprężenia i odkształcenia

12. Podaj definicję prostych przypadków obciążenia: rozciągania/ściskania, skręcania, zginania i ścinania.

osiowym rozciąganiem lub ściskaniem pręta pryzmatycznego nazywamy przypadek jego obciążenia dwiema równymi siłami, posiadającymi przeciwne zwroty, przyłożonymi w końcowych przekrojach pręta i działającymi wzdłuż jego osi, jeśli siły te skierowane są na zewnątrz przekrojów końcowych jest to rozciąganie, w przypadku przeciwnym - ściskanie

zginanie proste - nazywamy przypadek odciążenia, przy którym płaszczyzna obciążenia, przechodząca przez oś wzdłużną pręta, przechodzi także przez jedną z głównych centralnych osi bezwładności pola przekroju poprzecznego

czystym ścinaniem nazywamy stan, gdy na wszystkie ściany myślowo wyciętego elementu prostopadłościennego działają tylko naprężenia styczne przeciwstawiające się ścinaniu, element pod wpływem działania naprężeń stycznych zmienia swoją początkową postać

czystym skręcaniem nazywamy przypadek gdy siły wewnętrzne w przekroju poprzecznym pręta sprowadzają się do wektora momentu prostopadłego do płaszczyzny tego przekroju

Charakterystyki geometryczne przekroju

13. Jak określamy środek ciężkości pola figury płaskiej?

gdzie M_y, M_x są momentami statycznymi figury względem osi i momentu odśrodkowego

14. Podaj definicję momentów bezwładności figury względem osi i momentu odśrodkowego.

moment bezwładności:
- iloczyn elementarnego pola i kwadratu jego odległości od obranej osi, a całkowanie obejmuje całe pole S przekroju pęta

moment odśrodkowy:
- każde elementarne pole mnożone przez iloczyn jego współrzędnych prostokątnych, a sumowanie (całkowanie) rozciąga się przez całe pole S przekroju

15. Kiedy odśrodkowy moment bezwładności jest równy zeru?

gdy jedna z osi układu jest osią symetrii

16. Co to jest promień bezwładności figury?

promień bezwładności - ramię, a jego wymiarem jest długość wyrażona w m lub cm. Promień bezwładności względem osi x, y definiuje się następującymi zależnościami:

17. Jak zmieniają się momenty bezwładności figury przy równoległym przesunięciu osi układu współrzędnych?

gdzie a, b - współrzędne przesunięcia;

S - pole figury

M_i - moment statyczny

18. Jak zmieniają się momenty bezwładności figury przy obrocie osi układu współrzędnych?

19. Zdefiniuj osie główne i osie centralne przekroju.

osie główne - ułożenie osi układu w miejscu, w którym moment odśrodkowy jest równy zero, a osiowe momenty bezwładności osiągają wartości ekstremalne

osie centralne - przechodzące przez środek ciężkości układu

20. Zdefiniuj główne momenty bezwładności przekroju.

główny moment bezwładności - moment bezwładności liczony względem osi głównych

21. Do czego służy konstrukcja koła Mohra momentów bezwładności? Narysuj koło Mohra momentów bezwładności, zaznacz i opisz punkty charakterystyczne.

Konstrukcja koła Mohra służy do graficznego wyznaczania kierunków i wartości głównych momentów bezwładności na podstawie znajomości osiowych.

Klasyfikacja obciążeń

22. Narysuj układ sił przekrojowych zredukowanych do momentu głównego i wektora głównego. Jak nazywają się składowe tych wektorów ?

23. Wymień przypadki obciążeń prostych elementów konstrukcyjnych.

• rozciąganie lub ściskanie

• zginanie

• skręcanie

• ścinanie

24. Wymień przypadki obciążeń złożonych elementów konstrukcyjnych.

• zginanie ukośne prętów prostych

• zginanie z rozciąganiem lub ściskaniem

• mimośrodowe ściskanie lub rozciąganie

• zginanie ze skręcaniem

• zginanie belek z udziałem sił poprzecznych

25. Jak nazywane są jednowymiarowe elementy konstrukcyjne poddane działaniu:
    rozciągania/ściskania, zginania, skręcania?

Rozciąganiu/ściskanie - pręt

zginanie - belka

skręcanie - wałek

Rozciąganie i ściskanie

26. Podaj definicję granicy proporcjonalności, granicy plastyczności, wytrzymałości doraźnej i wytrzymałości na rozerwanie, pokaż te wielkości na wykresie naprężenie-odkształcenie dowolnie wybranego materiału.

granica proporcjonalności - granica do której próbka zachowuje się zgodnie z prawem Hooke'a (wydłużenie jest wprost proporcjonalne do naprężenia)

granica plastyczności - wartość R_e, naprężenie rozciągające, po osiągnięciu, którego następuje wyraźny wzrost wydłużenia rozciąganej próbki bez wzrostu siły

wytrzymałość doraźna - naprężenie R_m, po wystąpieniu którego następuje zniszczenie pręta (występuje miejscowe zwężenie przekroju próbki)

wytrzymałość na rozerwanie - naprężenie R_u, jest to naprężenie rzeczywiste występujące w przekroju poprzecznym próbki bezpośrednio przed jej zerwaniem w miejscu szyjki utworzonej w części pomiarowej

27. Na czym polega wzmocnienie materiału występujące w próbie rozciągania?

28. Jaka jest różnica pomiędzy odkształceniem sprężystym i trwałym materiału?

odkształcenie sprężyste - gdy odkształcenie ciała zanika po usunięciu obciążenia tj. kształt i wymiary ciała powracają do stanu przed obciążeniem

odkształcenie trwałe (plastyczne) - ma charakter trwały tj. pierwotne wymiary i kształt ciała ulegają zmianie

29. Podaj definicję naprężenia dopuszczalnego.

naprężenie dopuszczalne - iloraz naprężenia niebezpiecznego dla danego materiału i współczynnika bezpieczeństwa n. Wartość naprężenia niebezpiecznego przyjmuje się zazwyczaj jako równe wytrzymałości na rozciąganie lub ściskanie albo jako równe wartości granicy plastyczności dla danego obciążenia.

30. Podaj prawo Hooke'a dla jednowymiarowego stanu naprężenia.

Wydłużenie Δl pręta pryzmatycznego jest wprost proporcjonalne do siły rozciągającej P i do długości początkowej l₀ pręta, a odwrotnie proporcjonalne do pola przekroju poprzecznego pręta S.

31. Podaj definicję wydłużenia bezwzględnego i wydłużenia względnego.

wydłużenie względne: przyrost długości pomiarowej próbki po jego zerwaniu (L_u - L₀) odniesionej do początkowej długości pomiarowej próbki L_0, wyrażone w procentach

wydłużenie bezwzględne: przyrost długości pomiarowej próbki po jego zerwaniu
(L_u - L₀)

32. Podaj definicję i jednostkę modułu Younga.

moduł Younga - współczynnik sprężystości wzdłużnej, iloraz naprężenia przez odpowiadające mu skrócenie jednostkowe (E=σ/ε[...]), charakteryzuje zdolność materiału do powstania odkształceń podłużnych, w kierunku linii działania siły. Jest stałą materiałową

33. Podaj prawo o skurczu poprzecznym.

Jednostkowe odkształcenie poprzeczne jest proporcjonalne do jednostkowego odkształcenia podłużnego, a współczynnikiem proporcjonalności jest liczba Poissona zależna od rodzaju materiału

34. Podaj definicję współczynnika Poissona oraz jego wymiar i orientacyjne wartości jakie on przyjmuje dla metalowych materiałów izotropowych.

współczynnik Poissona (υ) - bezwzględna wartość ilorazu jednostkowego odkształcenia poprzecznego i jednostkowego odkształcenia podłużnego. Wartość współczynnika Poissona dla materiałów izotropowych zawiera się w granicach
<0 ; 0,5>, jest podobnie jak moduł sprężystości podłużnej stałą materiałową

35. Na czym polega metoda superpozycji i w jakich przypadkach nie można tej zasady stosować?

Metoda superpozycji polega na rozbiciu danego złożonego układu obciążeń na układy proste, tak dobrane, aby suma tych układów dała rozpatrywany układ Z zasady superpozycji wynika, że jeżeli między przyczyną, a skutkiem zachodzi zależność liniowa, to wtedy można rozpatrywać skutki kilku przyczyn równocześnie występujących w postaci sumy skutków pojedynczo i oddzielnie działających przyczyn. Zasada superpozycji ma jednak ograniczenia stosowalności. Nie można jej stosować, gdy naprężenia przekraczają granicę proporcjonalności oraz gdy działanie jednych sił zmienia charakter działania innych.

36. Z jakiego warunku (dodatkowego równania) należy skorzystać przy rozwiązywaniu zadań statycznie niewyznaczalnych?

Dodatkowym warunkiem jest ułożenie równania współzależności odkształceń, pamiętając, że ich liczba musi być równa liczbie wielkości statycznie niewyznaczalnych

37. Podaj wzór na wydłużenie pręta podgrzanego o Δt ?

∆l=αl∆t

38. Podaj zasady wymiarowania przekroju poprzecznego (określania wymiarów przekroju) z uwzględnieniem warunku wytrzymałościowego i warunku sztywności w przypadku rozciągania/ściskania

Zginanie

39. Podaj definicję zginania prostego i zginania czystego.

zginanie proste - nazywamy przypadek odciążenia, przy którym płaszczyzna obciążenia, przechodząca przez oś wzdłużną pręta, przechodzi także przez jedną z głównych centralnych osi bezwładności pola przekroju poprzecznego

zginanie czyste zachodzi w wypadku, gdy w myślowym przekroju pręta istnieje tylko moment zginający M_g, którego wektor jest prostopadły do osi pręta, czyli leży w płaszczyźnie przekroju.

40. Określ podstawowe założenia teorii zginania prętów.

• przekroje poprzeczne, płaskie przed odkształceniem, pozostają płaskie po odkształceniu;

• włókna wzdłużne nie wywierają na siebie nacisku, wskutek czego znajdują się w jednowymiarowym stanie naprężenia;

• odkształcenia włókien równoległych do osi pręta i znajdujących się w płaszczyźnie równoległej do warstwy obojętnej nie zależą od ich położenia w tej płaszczyźnie. Wynika stąd, że naprężenia normalne w punktach przekroju, znajdujących się w tej samej odległości od warstwy obojętnej, są takie same.

Zginanie występuje, gdy obciążenie pręta stanowi układ sił przecinających jego oś i do tej osi prostopadłych. Zakładamy, że układ ten jest płaski. Składa się on z sił czynnych P₁, P₂...i sił biernych - reakcji R i H.

41. Co to jest warstwa obojętna, oś obojętna?

Warstwa obojętna - płaszczyzna, w której położone są włókna materiału belki nie ulegające zmianą długości. Stanowi ona jednocześnie miejsce geometryczne osi obojętnych przekrojów poprzecznych belki.

Oś obojętna - jest centralną osią przekroju prostopadłą do płaszczyzny zgięcia, jest prostą przecięcia się warstwy obojętnej z płaszczyzną pola przekroju poprzecznego belki.

42. Zapisz równania równowagi elementu belkowego o nieskończenie małej długości poddanego działaniu sił tnących i momentów zginających.

43. Określ wartość momentu zginającego działającego na nieskończenie mały element pola przekroju dS , znajdujący się w odległości x₂ od środka obrotu, w których określono wartość momentu zginającego σ.

44. Podaj związek różniczkowy wiążący intensywność obciążenia ciągłego z siłą poprzeczną.

Pochodna względem x funkcji siły poprzecznej równa jest ujemnej wartości funkcji natężenia obciążenia ciągłego

45. Podaj związek różniczkowy wiążący intensywność obciążenia ciągłego z momentem zginającym.

46. Podaj związek różniczkowy wiążący natężenie obciążenia ciągłego z momentem zginającym.

47. Podaj związek pomiędzy naprężeniem normalnym i krzywizną pręta w przypadku czystego zginania.

ς - promień krzywizny pręta

48. Podaj wzór na maksymalne naprężenie normalne występujące przy czystym zginaniu.

49. Podaj związek pomiędzy naprężeniem normalnym i momentem zginającym w przypadku czystego zginania.

Wartość naprężenia w danym włóknie jest proporcjonalna do momentu gnącego.

50. Narysuj wykres naprężeń normalnych przy zginaniu, podaj wzory na wartość naprężeń: w dowolnym włóknie , w włóknie skrajnym, zdefiniuj wskaźnik wytrzymałości przy zginaniu

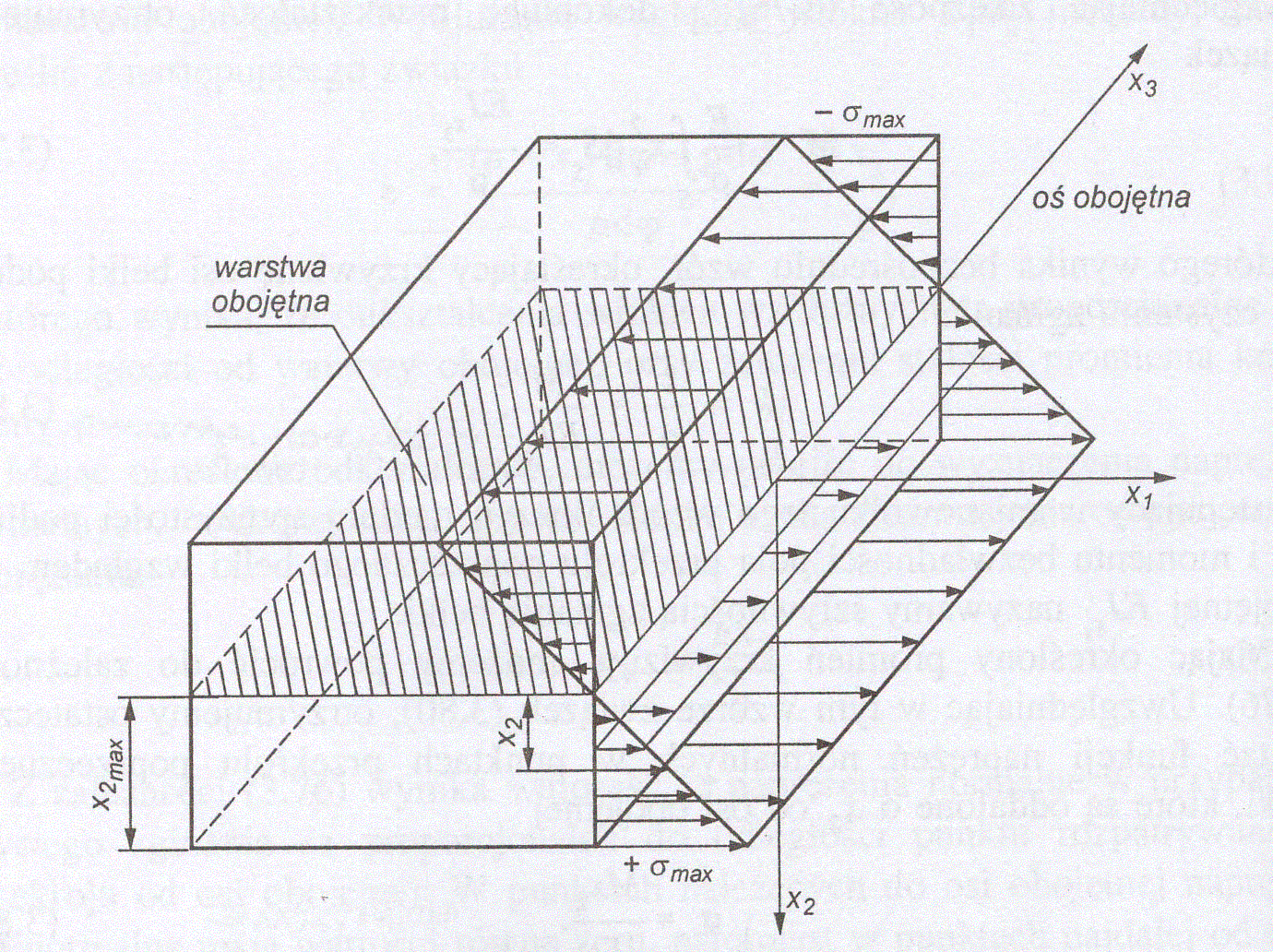
naprężenie:

- w dowolnym włóknie:

- maksymalne (w włóknie skrajnym)

wskaźnik wytrzymałości na zginanie:

51. Podaj zasady wymiarowania przekroju poprzecznego (określania wymiarów przekroju) z uwzględnieniem warunku wytrzymałościowego i warunku sztywności w przypadku zginania

Skręcanie

52. Podaj definicję siły przekrojowej - momentu skręcającego.

moment skręcający w danym przekroju poprzecznym pręta jest sumą algebraiczną momentów wszystkich par sił zewnętrznych, działających po jednej stronie tego przekroju i leżących w płaszczyznach prostopadłych do osi pręta

53. Określ podstawowe założenia teorii skręcania prętów.

• w przekrojach poprzecznych, prostopadłych do osi wałka, działają tylko naprężenia styczne

• przekroje poprzeczne wałka, płaskie przed odkształceniem, pozostają po odkształceniu przekrojami płaskimi

• promienie przekrojów poprzecznych wałka po odkształceniu pozostają odcinkami linii prostych

54. Podaj definicję kąta skręcenia i kąta odkształcenia postaciowego.

kątem skręcenia danego przekroju poprzecznego wałka (lub pręta) nazywamy względny kąt obrotu tego przekroju względem innego przekroju, który jest utwierdzony, bądź o którym zakładamy, że jest utwierdzony myślowo

kąt odkształcenia postaciowego:
(φ - kąt obrotu promienia, x - długość wałka), kąt o który pochyli się tworząca w wyniku skręcania

55. Określ wartość momentu skręcającego działającego na nieskończenie mały element pola przekroju dS , znajdujący się w odległości ρ od środka obrotu, w których określono wartość momentu skręcającego τ_ρ .

56. Narysuj wykres naprężeń stycznych przy skręcaniu, podaj wzory na wartość naprężeń: w dowolnym włóknie , w włóknie skrajnym, zdefiniuj wskaźnik wytrzymałości przy skręcaniu.

naprężenia:

• w dowolnym włóknie:
  

• w włóknie skrajnym:
  

wskaźnik wytrzymałości przy skręcaniu:
, gdzie: I₀ - moment bezwładności przekroju poprzecznego względem jego środka ciężkości, r_max - największa odległość tego punktów tego przekroju od jego środka

57. Podaj wzory na pracę i moc momentu skręcającego.

praca:
[kGm] (φ - kąt obrotu)

moc:
gdzie n - ilość obrotów

58. Podaj zasady wymiarowania przekroju poprzecznego (określania wymiarów przekroju) z uwzględnieniem warunku wytrzymałościowego i warunku sztywności w przypadku skręcania

Ścinanie

59. Podaj definicję stanu czystego ścinania, odkształcenia postaciowego.

czystym ścinaniem nazywamy stan, gdy na wszystkie ściany myślowo wyciętego elementu prostopadłościennego działają tylko naprężenia styczne przeciwstawiające się ścinaniu, element pod wpływem działania naprężeń stycznych zmienia swoją początkową postać

odkształcenie postaciowe występuje gdy objętość elementu pod wpływem obciążenia nie ulegnie zmianie, lecz zmieni się jego kształt

60. Podaj związek pomiędzy kątem odkształcenia postaciowego i jednostkowym wydłużeniem względnym w przypadku czystego ścinania

61. Podaj definicję modułu sprężystości postaciowej.

62. Podaj definicję prawa Hooke'a dla czystego ścinania

63. Jakie elementy konstrukcyjne poddane są naprężeniom ścinającym (ścinanie technologiczne) ?

• połączenia nitowane

• połączenia sworzniowe

• połączenia śrubowe

• połączenia spawane

64. Jakie rodzaje obciążenia występują w kolejnych etapach ścinania technologicznego?

• w stadium początkowym cięcia występuje ściskanie

• następnie ściskanie i rozrywanie

• ścinanie występuje w nieznacznym stopniu

65. Określ wartość średniego naprężenia ścinającego oraz średniego docisku działających na śrubę, nit w przypadku ścinania technologicznego.

średnie naprężenie ścinające:

średni docisk:

66. Podaj zasady wymiarowania przekroju poprzecznego (określania wymiarów przekroju) z uwzględnieniem warunku wytrzymałościowego i warunku sztywności w przypadku ścinania technologicznego.

Wytrzymałość złożona

67. Podaj definicję i narysuj schemat sił przekrojowych w przypadku zginania ukośnego, zginania z udziałem siły poprzecznej i zginania ze skręcaniem.

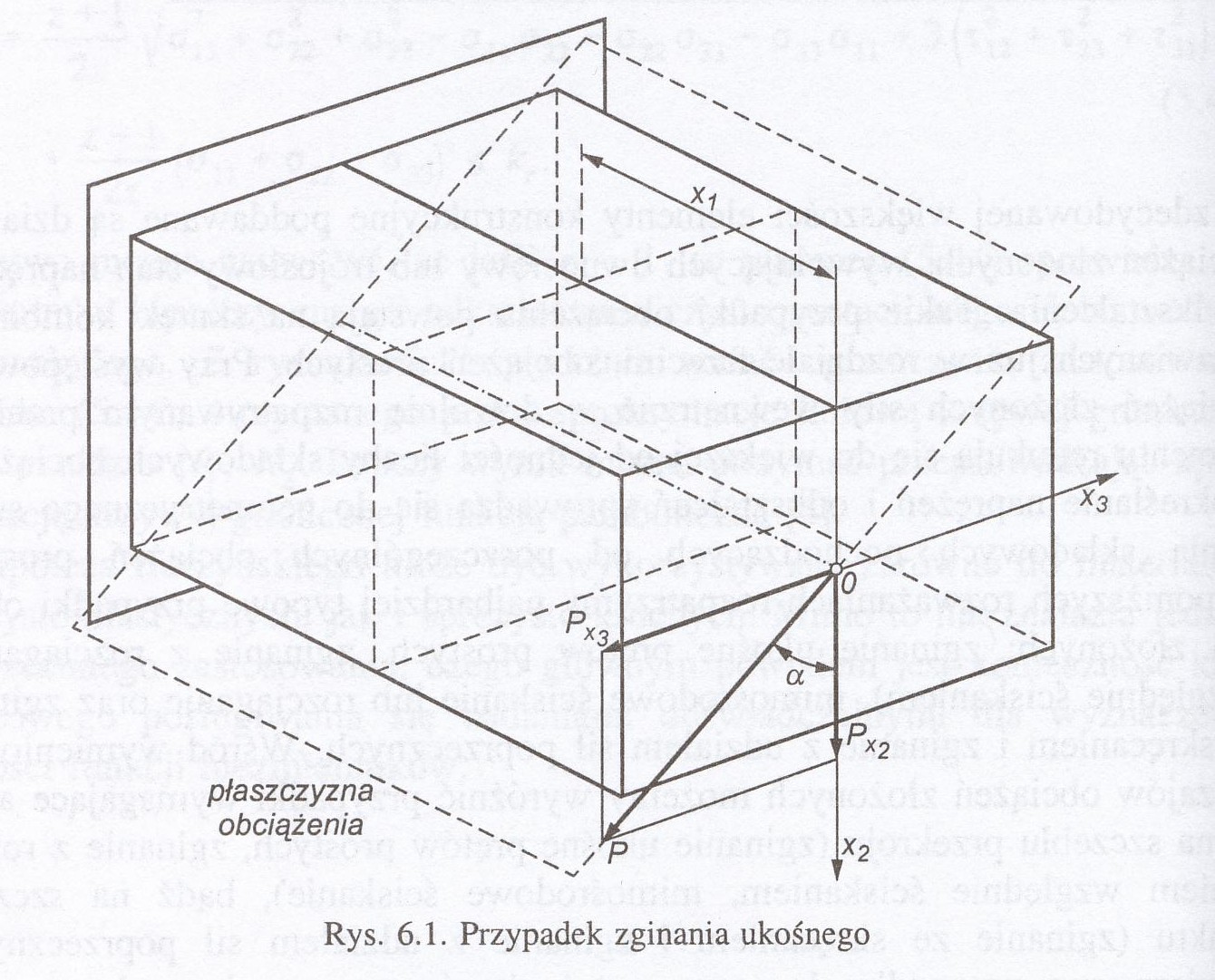
zginaniem ukośnym nazywamy przypadek obciążenia, przy którym płaszczyzna obciążenia, przechodząca przez oś wzdłużną pręta, nie przechodzi przez żadną z centralnych osi bezwładności pola przekroju poprzecznego

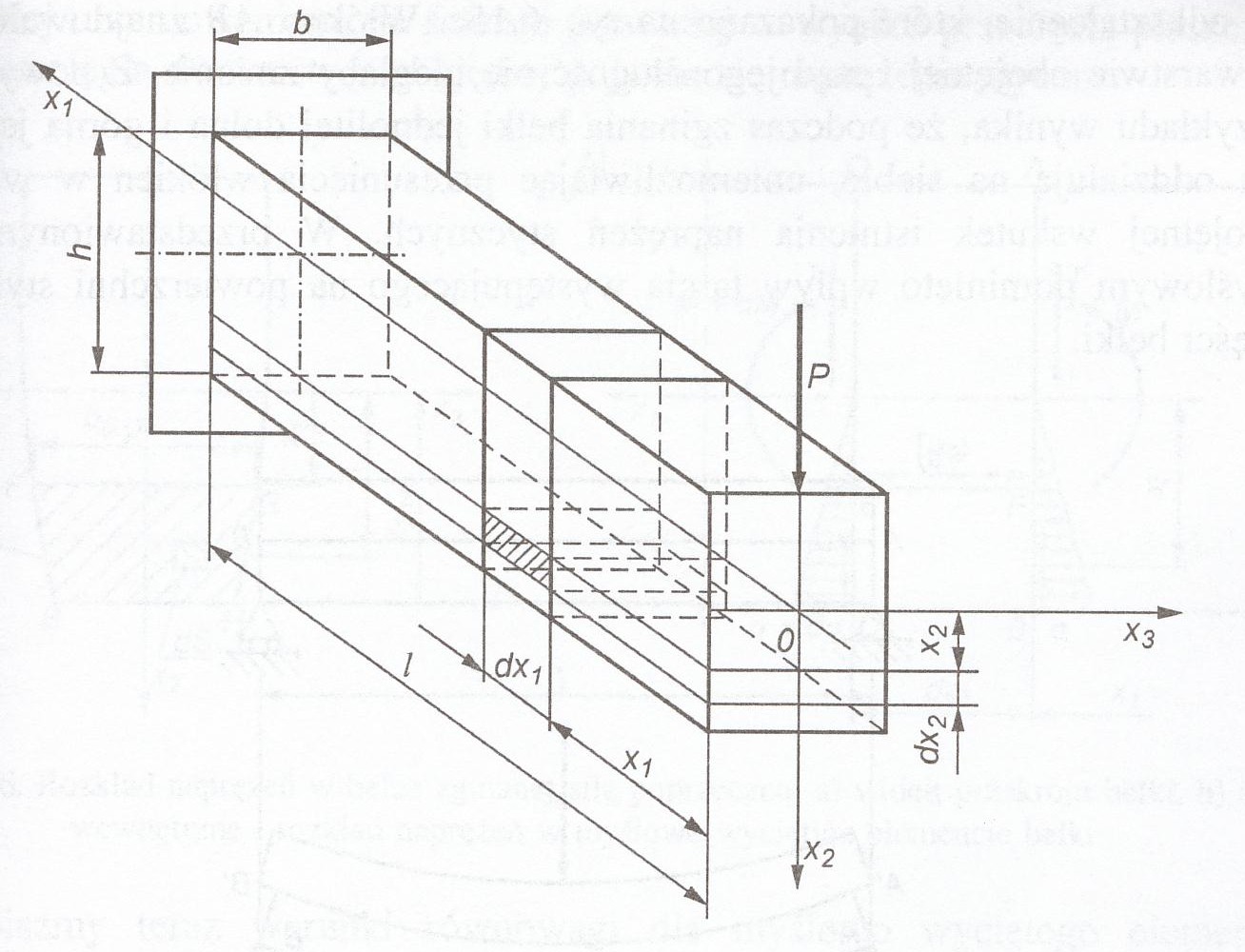
zginaniem z udziałem siły poprzecznej nazywamy przypadek, przy którym obciążenie stanowi moment zginający i siły poprzeczne

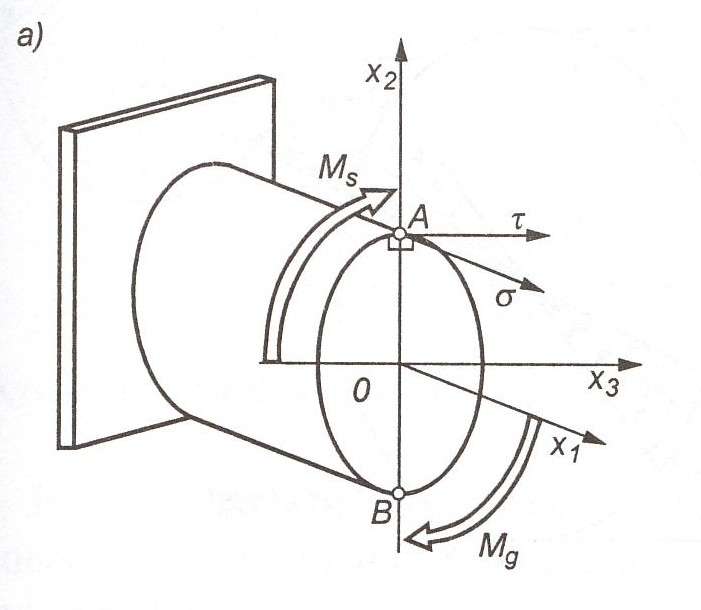
zginaniem ze skręcaniem nazywamy przypadek jednoczesnego wystąpienia zginania i skręcania.

68. Jak jest różnica pomiędzy zginaniem z rozciąganiem/ściskaniem a mimośrodowym rozciąganiem/ściskaniem?

zginanie z rozciąganiem lub ściskaniem występuje w przypadku, gdy siła skupiona przyłożona została w przekroju swobodnym pręta działa w płaszczyźnie przekroju i jest przesunięta względem środka ciężkości pola poprzecznego przekroju

mimośrodowe ściskanie lub rozciąganie występuje wówczas, gdy pręt obciążony jest siłą równoległą do jego osi, ale jednocześnie płaszczyzna obciążenia nie przechodzi przez żadną z dwóch głównych centralnych osi bezwładności przekroju

69. Określ wartości składowych momentu zginającego w ogólnym przypadku mimośrodowego ściskania, zginania ukośnego.

mimośrodowe ściskanie:

zginanie ukośne:

70. Wyprowadź wzór na naprężenie normalne w dowolnym punkcie przekroju obciążonego momentem
    (przypadek zginania ukośnego).

71. Wyprowadź wzór określający:

• kąt nachylenia osi obojętnej do osi układu współrzędnych

• równanie osi obojętnej

w przekroju obciążonym momentem
(przypadek zginania ukośnego).

kąt nachylenia osi obojętnej (β):

równanie osi obojętnej:

72. Wyprowadź wzór na naprężenie normalne w dowolnym punkcie przekroju w przypadku mimośrodowego ściskania.

gdzie B jest punktem przyłożenia siły P.

73. Co to jest rdzeń przekroju, podaj warunek z którego można wyznaczyć położenie rdzenia przekroju.

rdzeń przekroju - obszar, wewnątrz którego należy umieścić siłę P, aby powstały w pręcie naprężenia wyłączne jednego znaku. Przy odpowiednim doborze współrzędnych punktu przyłożenia siły P oś obojętna przejdzie stycznie do konturu przekroju i wtedy w każdym punkcie przekroju naprężenia będą jednego znaku.

74. Wyprowadź wzór określający równanie osi obojętnej w przypadku mimośrodowego ściskania.

75. Narysuj wykres zredukowanych naprężeń normalnych jako sumy naprężeń od zginania i ściskania w przypadku mimośrodowego rozciągania/ściskania podaj odpowiednie wzory, przyjąć punkt zaczepienia siły normalnej na osi głównej centralnej przekroju.

76. Podaj ogólny wzór na wartość zredukowanych naprężeń normalnych w ogólnym przypadku mimośrodowego ściskania.

77. Narysuj wykresy naprężeń normalnych i stycznych oraz określ punkty najbardziej wytężony przekroju w przypadku zginania ze skręcaniem.

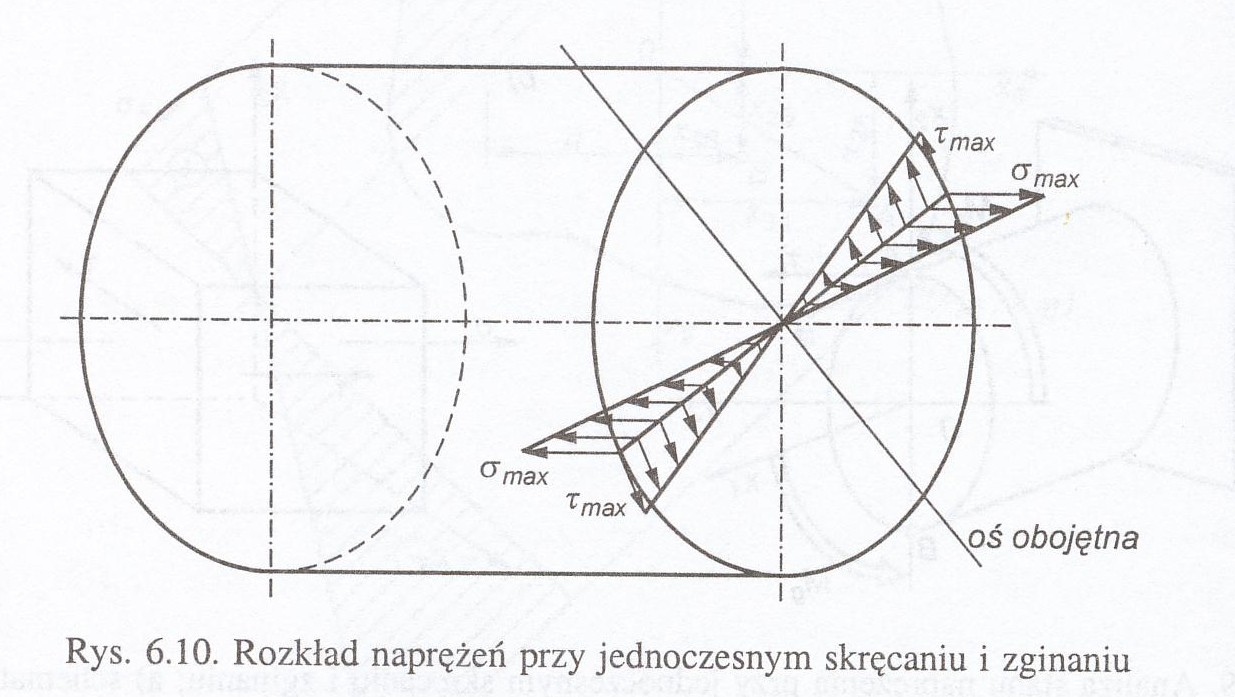
Największą wartość wytężenia otrzymujemy dla punktu przekroju, w którym naprężenia osiągają największe wartości.

78. W przypadku zginania ze skręcaniem podaj warunek wytrzymałościowy, wg hipotezy energii właściwej odkształcenia czysto postaciowego, z uwzględnieniem składowych ogólnych naprężenia.

79. W przypadku zginania ze skręcaniem podaj warunek wytrzymałościowy hipotezy największych naprężeń stycznych, zapisany w składowych głównych i ogólnych naprężenia.

80. W przypadku zginania ze skręcaniem podaj warunek wytrzymałościowy hipotezy energii odkształcenia czysto postaciowego, zapisany w składowych ogólnych naprężenia.

(pyt 78)

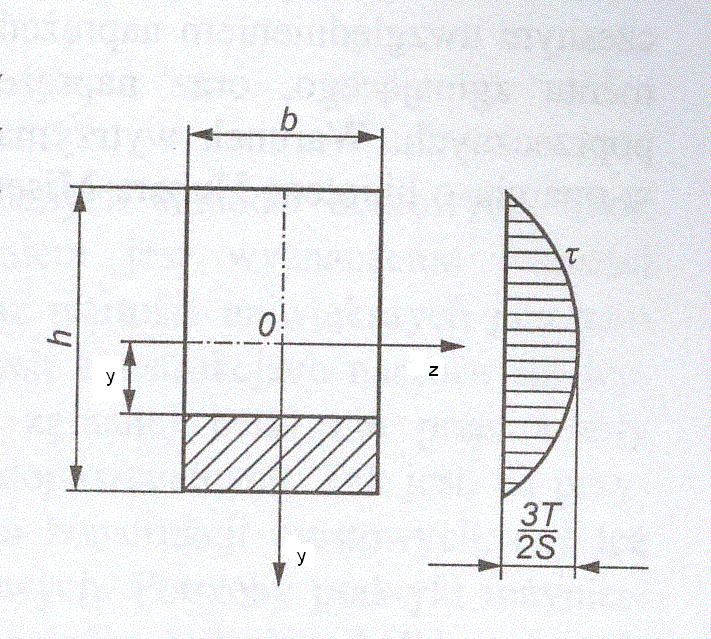
81. Podaj wzór Żurawskiego, określający wielkość naprężenia stycznego dowolnego przekroju obciążonego siłą poprzeczną T, wielkości występujące we wzorze wyjaśnij na rysunku.

82. 
    
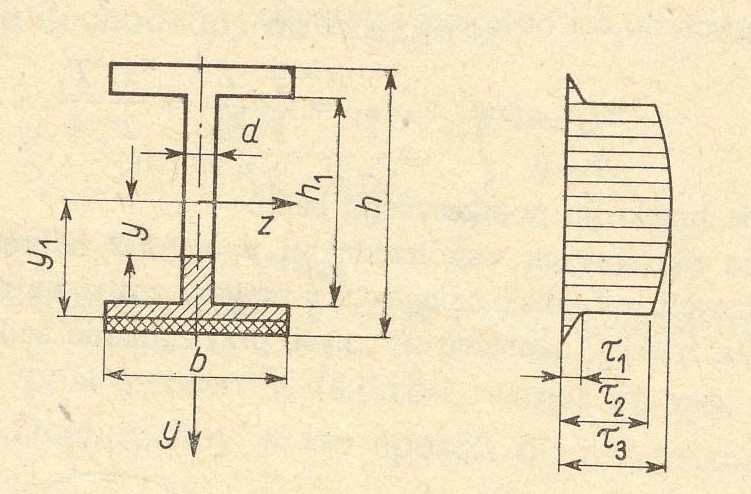
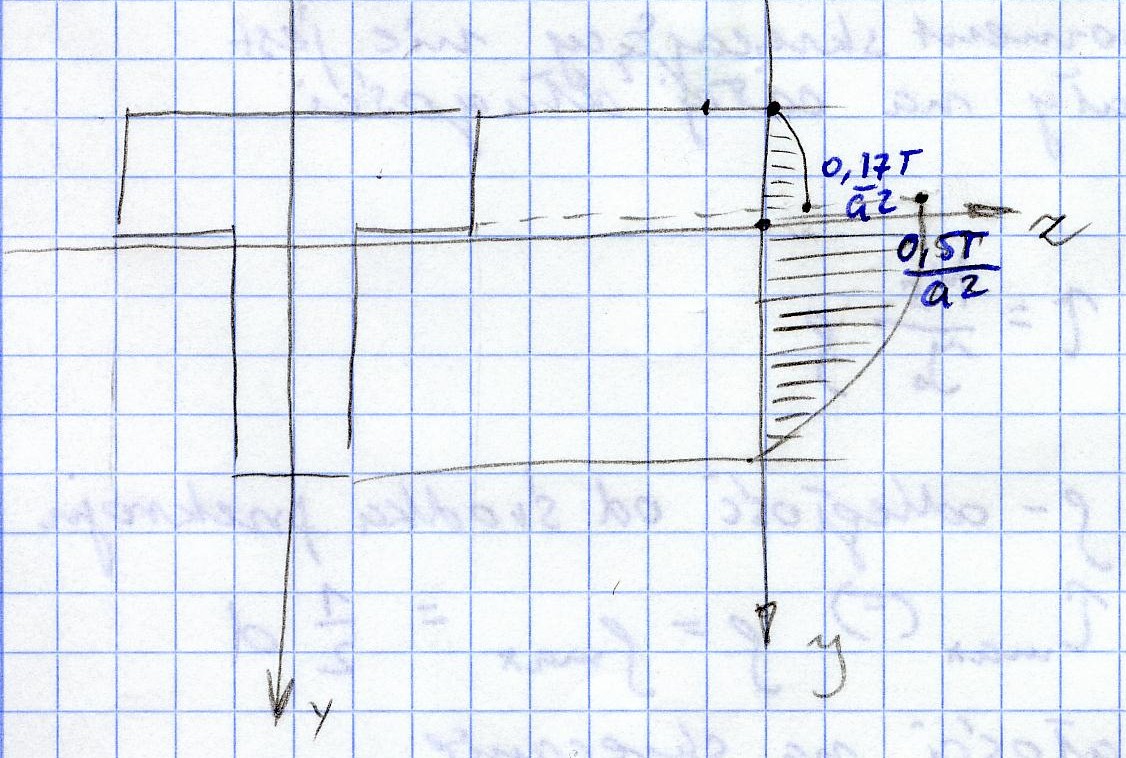
    Narysuj wykresy naprężeń stycznych przekroju teowego i dwuteowego, obciążonego siłą poprzeczną T.

Jednowymiarowy, dwuwymiarowy stan naprężenia i odkształcenia

83. Narysuj płaski element prostokątny poddany jednowymiarowemu stanowi obciążenia

• zapisz równania równowagi sił dla dowolnego przekroju nachylonego pod kątem α do kierunków głównych oraz wyznacz wartość naprężenia normalnego i stycznego w tym przekroju.

• 
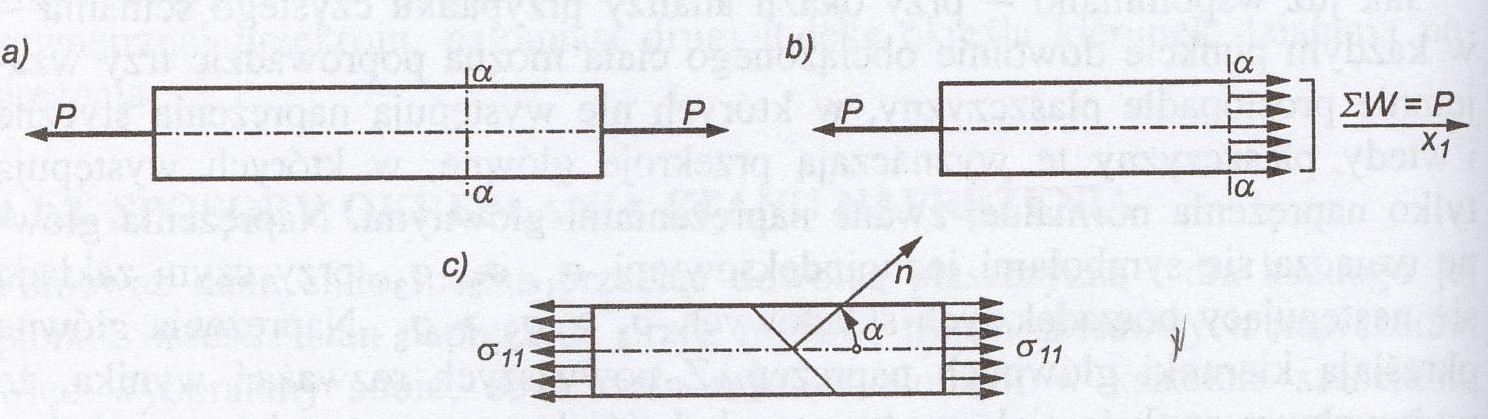
  pod jakim kątem jest nachylona płaszczyzna największego naprężenia stycznego, jaka jest wartość naprężeń normalnych i stycznych w tej płaszczyźnie

Przekrój ukośny:

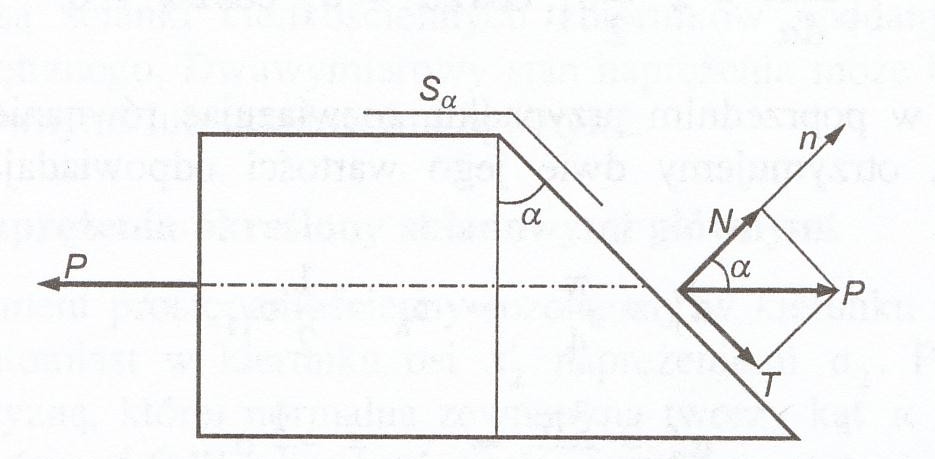
N = Pcosα

T = Psinα

naprężenie normalne:

naprężenie styczne:

84. Narysuj płaski element prostokątny, którego boki są obciążone składowymi głównym obciążenia (dwuwymiarowy stan obciążenia):

• zapisz równania równowagi sił dla dowolnego przekroju nachylonego pod kątem α do kierunków głównych oraz wyznacz wartość naprężenia normalnego i stycznego w tym przekroju.

• pod jakim kątem jest nachylona płaszczyzna największego naprężenia stycznego, jaka jest wartość naprężeń normalnych i stycznych w tej płaszczyźnie

równania równowagi:

naprężenie normalne:

naprężenie styczne:

maksymalne naprężenie styczne:

naprężenie normalne dla α=π/4:

85. Narysuj płaski element prostokątny, którego boki są obciążone składowymi ogólnymi obciążenia (dwuwymiarowy stan obciążenia):

• zapisz równania równowagi sił działających na przekrój nachylony pod kątem α do kierunków głównych, wyznacz wartość naprężenia normalnego i stycznego w tym przekroju

• podaj definicję wartości i kierunków naprężeń głównych

równania równowagi:

naprężenie normalne:

naprężenie styczne:

kierunki naprężeń głównych określa zależność :

wartości naprężeń głównych definiowane są jako:

86. Do czego służy konstrukcja koła Mohra stanu naprężenia. Narysuj koło Mohra dla dwuwymiarowego stanu naprężenia, zaznacz i opisz punkty charakterystyczne, jaki jest dodatni zwrot naprężenia stycznego.

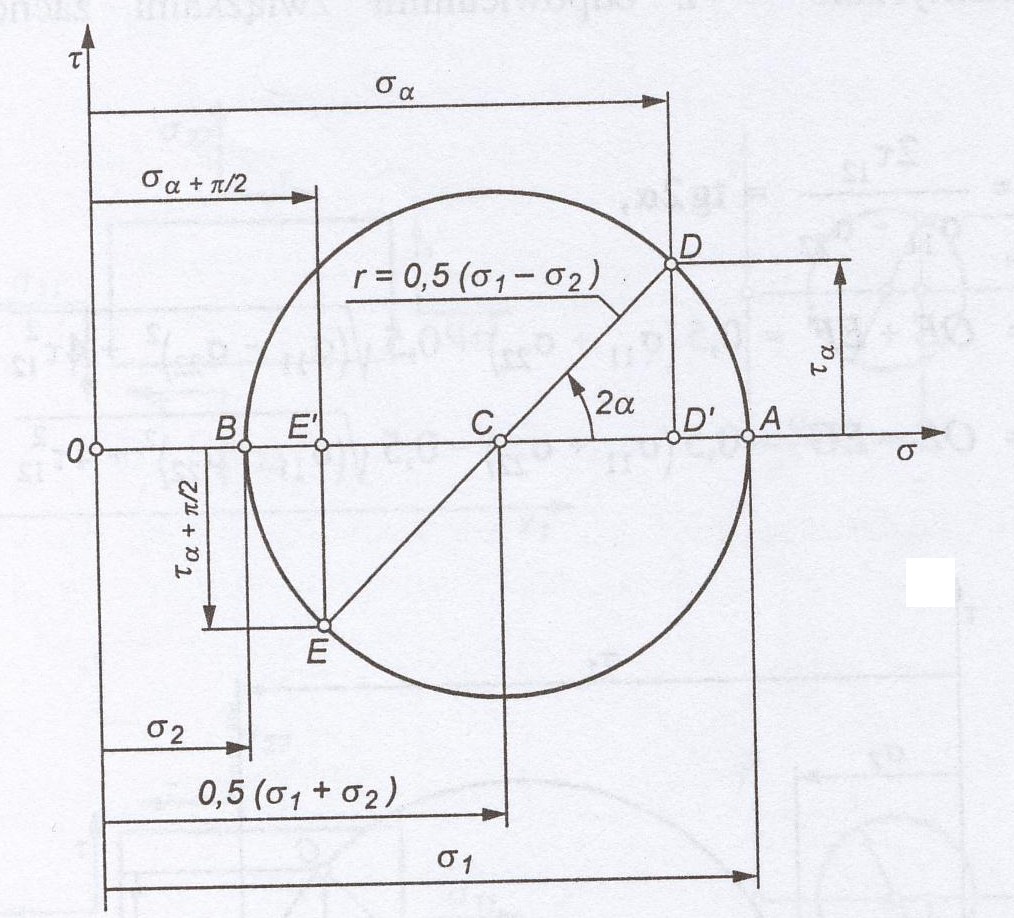
Konstrukcja Mohra służy do wykreślnego zilustrowania zależności między składowymi naprężenia w dowolnie wybranym przekroju.

87. Zapisz związki określające jednostkowe odkształcenie w kierunku osi układu współrzędnych w przypadku dwuwymiarowego stanu naprężenia.

odkształcenie w kierunku osi x:

odkształcenie w kierunku osi y:

Trójwymiarowy stan naprężenia i odkształcenia

88. Narysuj wektor naprężenia i jego składowe w ogólnym przypadku położenia wektora, nazwij składowe wektora naprężenia Jakie płaszczyzny (przekroje) nazywamy głównymi?

89. Na ściankach elementarnego sześcianu zaznacz wektory naprężeń normalnych i stycznych, zapisz macierz składowych stanu naprężenia w punkcie dla trójwymiarowego stanu naprężenia, zapisz związki naprężeń stycznych wynikające z zasady wzajemności naprężeń stycznych.

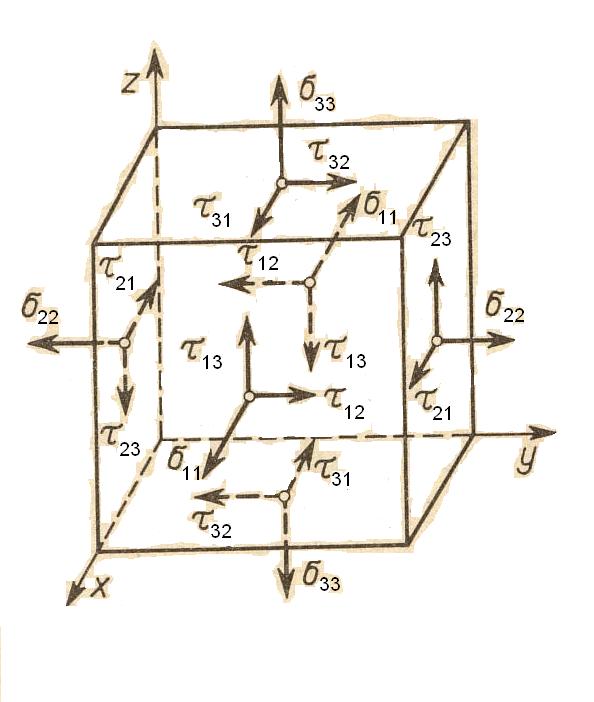
Stan naprężenia:

90. Na ściankach elementarnego sześcianu zaznacz wektory naprężeń głównych, zapisz macierz składowych stanu naprężenia w punkcie dla stanu trójwymiarowego stanu naprężenia wyrażonego w składowych głównych.

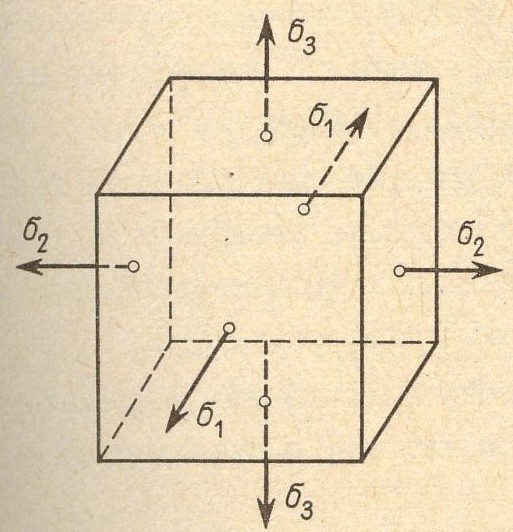
91. Zapisz uogólnione prawo Hooke'a wyrażone w ogólnych składowych naprężenia, dla przypadków dwuwymiarowego i trójwymiarowego stanu naprężenia.

dwuwymiarowy stan naprężenia:

trójwymiarowy stan naprężenia:

92. Zapisz uogólnione prawo Hooke'a wyrażone w składowych głównych naprężenia, dla przypadków dwuwymiarowego i trójwymiarowego stanu naprężenia.

dwuwymiarowy stan naprężenia:

trójwymiarowy stan naprężenia:

93. Zapisz wzór na jednostkową zmianę objętości ciała izotropowego:

1. wyrażoną w składowych stanu odkształcenia:
   

2. wyrażoną w składowych stanu naprężenia:
   

Energia odkształcenia sprężystego

94. Podaj definicję energii właściwej odkształcenia sprężystego, energii odkształcenia czysto objętościowego i energii odkształcenia czysto postaciowego.

energii właściwej odkształcenia sprężystego - energia nagromadzona w materiale w wyniku odkształceń sprężystych, wywołanych działaniem sił wewnętrznych odniesiona do objętości rozpatrywanego elementu

energii odkształcenia czysto objętościowego - część energii odkształcenia sprężystego, która zostaje zużyta na wywołanie zmiany objętości ciała

energii odkształcenia czysto postaciowego - część energii odkształcenia sprężystego, która zostaje zużyta na wywołanie zmiany postaci ciała

95. Zakładając, że elementarny sześcian jest obciążony tylko naprężeniem
    , określ wielkość pracy, którą wykona siła
    powodująca wydłużenie sześcianu, w kierunku osi Ox₁ o długość λ₁₁.

96. Podaj wzór na energią właściwą odkształcenia sprężystego elementarnego sześcianu obciążonego tylko naprężeniem
    .

97. Zakładając, że elementarny sześcian jest obciążony tylko naprężeniem
    , określ wielkość pracy, którą wykona siła
    powodująca odkształcenie postaciowe elementarnego sześcianu określone kątem γ₂₃.

98. Podaj wzór na energią właściwą odkształcenia sprężystego elementarnego sześcianu obciążonego tylko naprężeniem
    .

99. Podaj wzór na całkowitą energię właściwą odkształcenia sprężystego:

1. jako funkcję składowych ogólnych stanu naprężenia i odkształcenia

2. jako funkcję tylko składowych ogólnych stanu naprężenia.

100. Podaj wzór na całkowitą energię właściwą odkształcenia sprężystego:

1. jako funkcję składowych głównych stanu naprężenia i odkształcenia

2. jako funkcję tylko składowych głównych stanu naprężenia.

101. Zdefiniuj pojęcie średniego naprężenia normalnego, jakie są odkształcenia elementarnego sześcianu poddanego obciążeniom o wartości średniego naprężenia normalnego, wyprowadź wzór na jednostkową zmianę objętości ciała izotropowego przy takim obciążeniu.

średnie naprężenie normalne:

odkształcenie poddane obciążeniom o wartości średniego naprężenia normalnego:

zmiana objętości ciała izotropowego:

102. Podaj wzór na energię właściwą odkształcenia czysto objętościowego:

1. wyrażoną w składowych ogólnych stanu naprężenia

2. wyrażoną w składowych głównych stanu naprężenia

103. Podaj wzór na energię właściwą odkształcenia czysto postaciowego:

1. wyrażoną w składowych ogólnych stanu naprężenia

2. wyrażoną w składowych głównych stanu naprężenia

Hipotezy wytężenia materiału

104. Podaj definicje wytężenia materiału i stanu niebezpiecznego, określ ogólne kryterium pojawienia się stanu niebezpiecznego materiału.

wytężenie materiału w punkcie elementu konstrukcyjnego rozumiemy stan fizykalny materiału, wywołany obciążeniem, określający stopień narażenia go na pojawienie się stanu niebezpiecznego

stan niebezpieczny materiału - utrata jego spójności lub pojawienie się w nim odkształceń trwałych. Może być określony przez wytrzymałość materiału R_m lub przez granicę plastyczności R_e lub przez umowną granicę plastyczności R₀₂

105. Zdefiniuj pojęcie naprężenia zredukowanego i naprężenia dopuszczalnego, podaj sformułowanie warunku wytrzymałościowego uwzględniający wymienione wielkości.

naprężenie zredukowane definiuje się jako funkcję wytężenia, odpowiadającą stanowi naprężenia panującemu w próbce rozciąganej, gdy naprężenia w tej próbce osiągają wartość naprężeń niebezpiecznych:

kryterium pojawienia się stany niebezpiecznego:

naprężenie dopuszczalne:
gdzie n - współczynnik bezpieczeństwa

warunek wytrzymałościowy:

106. Określ warunek stanu niebezpiecznego wg hipotezy największego naprężenia normalnego oraz zgodnie z tą hipotezą sformułuj warunek wytrzymałościowy dla stanu trójwymiarowego określonego składowymi głównymi stanu naprężenia.

(Miarą wytężenia materiału jest największe naprężenie normalne)

warunek stanu niebezpiecznego:

warunek wytrzymałościowy:

• rozciąganie:

• ściskanie:

107. Określ warunek stanu niebezpiecznego wg hipotezy największego odkształcenia jednostkowego oraz zgodnie z tą hipotezą sformułuj warunek wytrzymałościowy dla stanu trójwymiarowego określonego składowymi głównymi stanu naprężenia.

(Wartość największego odkształcenia jednostkowego dla danego złożonego stanu naprężenia nie może przekroczyć wartości dopuszczalnego odkształcenia jednostkowego, określonej na podstawie próby jednoosiowego rozciągania)

warunek stanu niebezpiecznego:

warunek wytrzymałościowy:

108. Określ warunek stanu niebezpiecznego wg hipotezy największych naprężeń stycznych oraz zgodnie z tą hipotezą sformułuj warunek wytrzymałościowy dla stanu trójwymiarowego określonego składowymi głównymi stanu naprężenia.

(Miarą wytężenia materiału jest największe naprężenie styczne)

warunek stanu niebezpiecznego:

warunek wytrzymałościowy:

109. Określ warunek stanu niebezpiecznego wg hipotezy energii właściwej odkształcenia sprężystego oraz zgodnie z tą hipotezą sformułuj warunek wytrzymałościowy dla stanu trójwymiarowego określonego składowymi głównymi stanu naprężenia.

(Miarą wytężenia materiału jest całkowita energia właściwa odkształcenia sprężystego)

warunek stanu niebezpiecznego:

warunek wytrzymałościowy:

110. Określ warunek stanu niebezpiecznego wg hipotezy energii odkształcenia czysto postaciowego oraz zgodnie z tą hipotezą sformułuj warunek wytrzymałościowy:

(Miarą wytężenia materiału jest energia sprężysta odkształcenia czysto postaciowego)

1. dla trójwymiarowego stanu naprężenia:

warunek stanu niebezpiecznego:

warunek wytrzymałościowy:

• określonego składowymi ogólnymi stanu naprężenia:

• określonego składowymi głównymi stanu naprężenia:

1. dla dwuwymiarowego stanu naprężenia:

• dla przypadku rozciągania ze skręcaniem
  :

• dla przypadku czystego ścinania
  :

111. Przedstaw schematycznie wykresy rozciągania (σ-ε) dla materiałów sprężysto-kruchego i sprężysto-plastycznego.

112. Jakie hipotezy wytrzymałościowe stosujemy w przypadku materiałów sprężysto-plastycznych a jakie przypadku materiałów sprężysto-kruchych?

Zarówno w przypadku materiałów sprężysto-plastycznych i sprężysto-kruchych może być wykorzystywana hipoteza Burzańskiego. Mimo to nie znalazła ona powszechnego zastosowania, czego głównym powodem jest konieczność każdorazowego posługiwania się badaniami doświadczalnymi dla wyznaczenia wartości funkcji niezmienników.

materiały sprężysto-kruche:

• hipoteza największego odkształcenia jednostkowego

materiały sprężysto-plastycznych:

• hipoteza największego naprężenia stycznego

• hipoteza energii odkształcenia czysto postaciowego

---