nr ćw. 108	data	Dariusz Jafra	Wydział Elektryczny	Semestr II	grupa I-2 1930-2100
prowadzący mgr K.Łapsa					przygotowanie	wykonanie	ocena końcowa

Temat: Wyznaczanie modułu Younga metodą ugięcia

Wiadomo że gdy na podłużny pręt działa siła prostopadle do jego długości, doznaje on ugięcia, a wielkość tzw. strzałki ugięcia S jest zawsze proporcjonalna do siły F, a także zależy od wymiarów geometrycznych pręta, sposobu jego mocowania i rodzaju materiału z którego jest on wykonany. Pręt na rysunku pod działaniem siły ugina się w ten sposób że górne warstwy pręta są rozciągane a dolne ściskane. W środku wysokości istnieje warstwa, której długość nie ulega zmianie. Przekroje prostopadłe pręta, przy braku obciążenia są wzajemnie równoległe, tworzą natomiast kąt
po przyłożeniu siły.

Na rysunku obok zaznaczyłem rozpatrywane przekroje przez 1 i 2 oraz kąt
między 1 i 2 (1' jest równoległym przesunięciem przekroju 1 do linii przecięcia warstwy neutralnej N z przekrojem 2).

Jeśli zacznę rozpatrywać element pręta o długości
, grubości
i szerokości b znajdujący się w odległości x od krawędzi zamocowanej i na wysokości y powyżej warstwy środkowej to na skutek ugięcia belki badana warstwa ulega ugięciu o
.

Zgodnie z prawem Hooke'a wydłużenie jest proporcjonalne do siły i długości początkowej oraz odwrotnie proporcjonalne do powierzchni przekroju

gdzie E - moduł Younga,
- siła rozciągająca badaną warstwę elementarną.

Taka sama siła, lecz przeciwnie skierowana, działa na warstwę elementarną położoną symetrycznie poniżej warstwy neutralnej N.

Moment siły
względem warstwy N wynosi

Całkowity moment M sił działających na wszystkie warstwy zawarte między przekrojami 1 i 2 obliczam całkując powyższe równanie względem y po całej grubości

(1)

Jeśli oznaczę

(2)

to równanie (1) mogę napisać w postaci

(3)

Równanie to otrzymałem rozpatrując odkształcenie pręta, którego bezpośrednią przyczyną jest siła F przyłożona do jego końca. Moment tej siły względem przekroju 2 wynosi lub zaniedbując wielkość
jako małą w porównaniu z x

(4)

Kąt
jest zawarty między stycznymi do pręta w punktach, gdzie przekroje 1 i 2 przecinają górną powierzchnię. Na podstawie rysunku mogę napisać następujący związek

Wstawiając powyższe równanie do wzoru (3) i porównując wzory (3) i (4) otrzymuję elementarną strzałkę ugięcia

Całkowitą strzałkę ugięcia otrzymuję całkując powyższe równanie po całej długości pręta

Po scałkowaniu, wyrażenie na całkowitą strzałkę ugięcia przyjmuje postać

Wartość współczynnika H zależy od kształtu i rozmiarów geometrycznych pręta. Gdy przekrój jest prostokątem o wysokości h i szerokości b, to całkowanie równania (2) prowadzi do wyniku

Całkowanie podobnego wyrażenia dla przekroju kołowego daje

Podstawiając wartości współczynników H otrzymuję odpowiednio dla obu przekrojów strzałki ugięcia

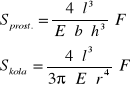
Otrzymane powyżej wzory odnoszą się do pręta jednostronnie obciążonego i jednym końcem umocowanego. Równania te mogę łatwo dostosować do sytuacji, gdy pręt jest swobodnie oparty dwoma końcami i obciążony w środku.

Zachowuje się on wtedy tak, jak gdyby był zamocowany w środku, a na jego końce działały siły
skierowane ku górze. Siła
działa wtedy na pręt o długości
.

Po uwzględnieniu tych warunków w poprzednich wzorach uzyskuję wzory na strzałki ugięcia prętów

dwustronnie podpartych

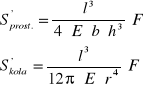
A z tych wzorów mogę już łatwo obliczyć moduł Younga. Po wykonaniu prostego przekształcenia mam moduł Younga dla przekroju prostokątnego

i dla przekroju kołowego

.

Przebieg doświadczenia

1. Zmierzyć wymiary poprzeczne pręta.

2. Zmierzyć odległości między krawędziami podpierającymi i wyznaczyć środek pręta.

3. Wypoziomować katetometr i przy jego pomocy wyznaczyć położenie górnej krawędzi pręta

nieobciążonego
.

4. Obciążając kolejno środek pręta ciężarkami (wg kolejności 1+2+3+4+5) odczytywać położenie

górnej krawędzi pręta.

5. Powtórzyć pomiary strzałki ugięcia przy zmniejszaniu obciążenia.

6. Narysować wykres strzałki ugięcia w funkcji obciążenia S=S(F).

7. Odczytać z wykresu strzałki ugięcia dla obciążeń 300g i 1600g Przeprowadzić obliczenia modułu

Younga dla tych obciążeń dla dwóch prętów.

8. Obliczyć wartości średnie modułu Younga E i oszacować błędy
.

Pomiary:

-Tabela pomiaru wymiar*w belek:

	Pr*t mosi*żny [mm]	Pr*t aluminiowy [mm]	P*askownik aluminiowy a [mm] b [mm]
1	7,86	7,9	7,86	7,84
2	7,85	7,9	7,86	7,84
3	7,84	7,88	7,88	7,86
4	7,86	7,9	7,88	7,86
5	7,88	7,92	7,86	7,86
6	7,86	7,9	7,88	7,86
7	7,87	7,88	7,9	7,88
8	7,86	7,9	7,9	7,88
9	7,88	7,88	7,9	7,88
10	7,88	7,92	7,9	7,88
srednia	7,864	7,898	7,882	7,864

-Tabela z pomiarmi strza*ek ugi*cia do wyznaczenia modu*u Younga dla

p*askownika aluminiowego:

m [kg]	s [mm]	Δs [mm]	a [mm]	b [mm]		E [N/m^2]		E*r [N/m^2]	ΔE*r [N/m^2]	EK [N/m^2]
0	627,48	0	7,864		7,882
0,2	627,05	0,43	7,864		7,882		8,135E+10
0,4	626,64	0,84	7,864		7,882		8,329E+10
0,5	626,37	1,11	7,864		7,882		7,878E+10
0,7	625,83	1,65	7,864		7,882		7,42E+10
0,9	625,42	2,06	7,864		7,882		7,641E+10
1	625,17	2,31	7,864		7,882		7,572E+10
1,2	624,68	2,8	7,864		7,882		7,496E+10
1,4	624,23	3,25	7,864		7,882		7,534E+10
1,5	624,02	3,46	7,864		7,882		7,582E+10
1,7	623,49	3,99	7,864		7,882		7,452E+10
1,9	623,23	4,25	7,864		7,882		7,819E+10	7,343E+10	4,361E+09	(7,34±0,34)E10
1,7	623,51	4,37	7,864		7,882		6,804E+10
1,5	624,03	3,85	7,864		7,882		6,814E+10
1,4	624,23	3,65	7,864		7,882		6,709E+10
1,2	624,66	3,22	7,864		7,882		6,518E+10
1	625,16	2,72	7,864		7,882		6,43E+10
0,9	625,41	2,47	7,864		7,882		6,373E+10
0,7	626,12	1,76	7,864		7,882		6,956E+10
0,5	626,69	1,19	7,864		7,882		7,349E+10
0,4	626,94	0,94	7,864		7,882		7,443E+10
0,2	627,44	0,44	7,864		7,882		7,95E+10
	627,88	0	7,864		7,882

-Tabela z pomiarmi strza*ek ugi*cia do wyznaczenia modu*u Younga dla

p*askownika aluminiowego:

m [kg]	s [mm]	Δs [mm]	r [mm]	E [N/m^2]	E*r [N/m^2]	ΔE*r [N/m^2]	EK [N/m^2]
0	626,16	0	7,864
0,2	625,52	0,64	7,864	5,84E+09
0,4	624,95	1,21	7,864	6,18E+09
0,5	624,59	1,57	7,864	5,95E+09
0,7	623,98	2,18	7,864	6E+09
0,9	623,49	2,67	7,864	6,3E+09
1	623,12	3,04	7,864	6,15E+09
1,2	622,62	3,54	7,864	6,34E+09
1,4	622,11	4,05	7,864	6,46E+09
1,5	621,85	4,31	7,864	6,51E+09
1,7	621,32	4,84	7,864	6,57E+09	6,44E+09	2,93E+08	(6,4±0.3)E+9
1,9	620,86	5,3	7,864	6,7E+09
1,7	621,42	4,87	7,864	6,53E+09
1,5	621,54	4,75	7,864	5,9E+09
1,4	622,25	4,04	7,864	6,48E+09
1,2	622,99	3,3	7,864	6,8E+09
1	623,41	2,88	7,864	6,49E+09
0,9	623,75	2,54	7,864	6,62E+09
0,7	624,19	2,1	7,864	6,23E+09
0,5	624,95	1,34	7,864	6,98E+09
0,4	625,21	1,08	7,864	6,92E+09
0,2	625,78	0,51	7,864	7,33E+09
0	626,29	0	7,864

-Opis tabel

m - masa obci*żnik*w zawieszanych na belce

s - odleg*o*ć punktu pomiarowego od punktu odniesienia

Δs - strza*ka ugi*cia ( r*żnica s-pocz*tkowego i s z danego pomiaru)

a,b,r- *rednie warto*ci wymiar*w belek

E - modu* Younga dla danego pomiaru

*) dla p*askownika aluminiowego

*) dla pr*ta mosi*żnego

`

E_*r - *rednia wrto*ć modu*u Younga dla wszystkich pomiar*w

ΔE_*r - odchlenie standardowe *redniej

-Odleg*o*ć mi*dzy podporami:

l = (650 ± 1 ) [mm]

Wnioski:

Wyniki przeprowadzonych pomiar*w s*