AKADEMIA GÓRNICZO - HUTNICZA im. Stanisława Staszica w Krakowie
Wydział: Inżynierii Mechanicznej i Robotyki
TEORIA STEROWANIA
Prowadzący: dr inż. Dariusz Grzybek
Student: Łukasz Kafel	Kierunek: Mechatronika	Ocena:
				Grupa: 25
				Numer indeksu: 215426

TEMAT ĆWICZENIA:

Badanie sterowalności i obserwowalności układów Nasze zadanie polegało na zbadaniu poniższego układu:

gdzie: Uw - napięcie wejściowe, Ul - napięcie wyjściowe

1. Modelowanie powyższego układu w środowisku MATLAB - SIMULINK

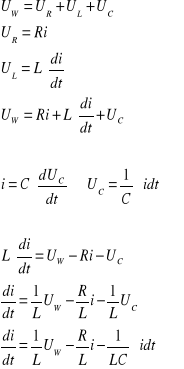
Poniżej przedstawiono układ zamodelowany w MATLAB - SIMULINKu

Wynik działania przy wymuszeniu skokiem jednostkowym

2. Modelowanie w przestrzeni stanów

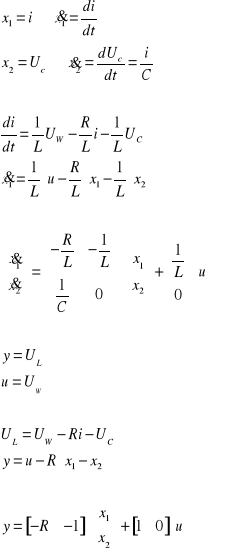
Po zbudowaniu następującego M-pliku:

A=[-10 -1;1 0]

B=[1;0]

C=[-10 -1]

D=[1]

Qs=ctrb(A,B)

rank(A)

rank(Qs)

Otrzymaliśmy następujący wynik:

Qs =

1 -10

0 1

ans =

2

ans =

2

Ponieważ rząd macierzy sterowania i macierzy sterowalności są sobie równe obiekt jest sterowalny

3. Badanie obiektu za pomocą STATE - SPACE

Otrzymaliśmy następujący wynik:

Wynik jest identyczny, model w przestrzeni stanów jest więc prawidłowy

4. Badanie obserwowalności układu

Stworzyliśmy następujący M-plik

A=[-10 -1;1 0]

B=[1;0]

C=[-10 -1]

D=[1]

Qo=obsv(A,C)

rank(A)

rank(Qo)

Wynikiem jest następujący:

A =

-10 -1

1 0

B =

1

0

C =

-10 -1

D =

1

Qo =

-10 -1

99 10

ans =

2

ans =

2

Ponieważ rząd macierzy sterowalności i obserwowalności są sobie równe układ jest obserwowalny

W drugim przypadku mamy co następuje:

A=[-10 -1;1 0]

B=[1;0]

C=[0 1]

D=[1]

Qo=obsv(A,C)

rank(A)

rank(Qo)

Wynikiem jest następujący:

Qo =

0 1

1 0

ans =

2

ans =

2

Podobnie rząd macierzy sterowalności i obserwowalności są sobie równe układ jest obserwowalny.

7

---