- 1 -

GEOMETRIA ANTENY PODŚWIETLANEJ

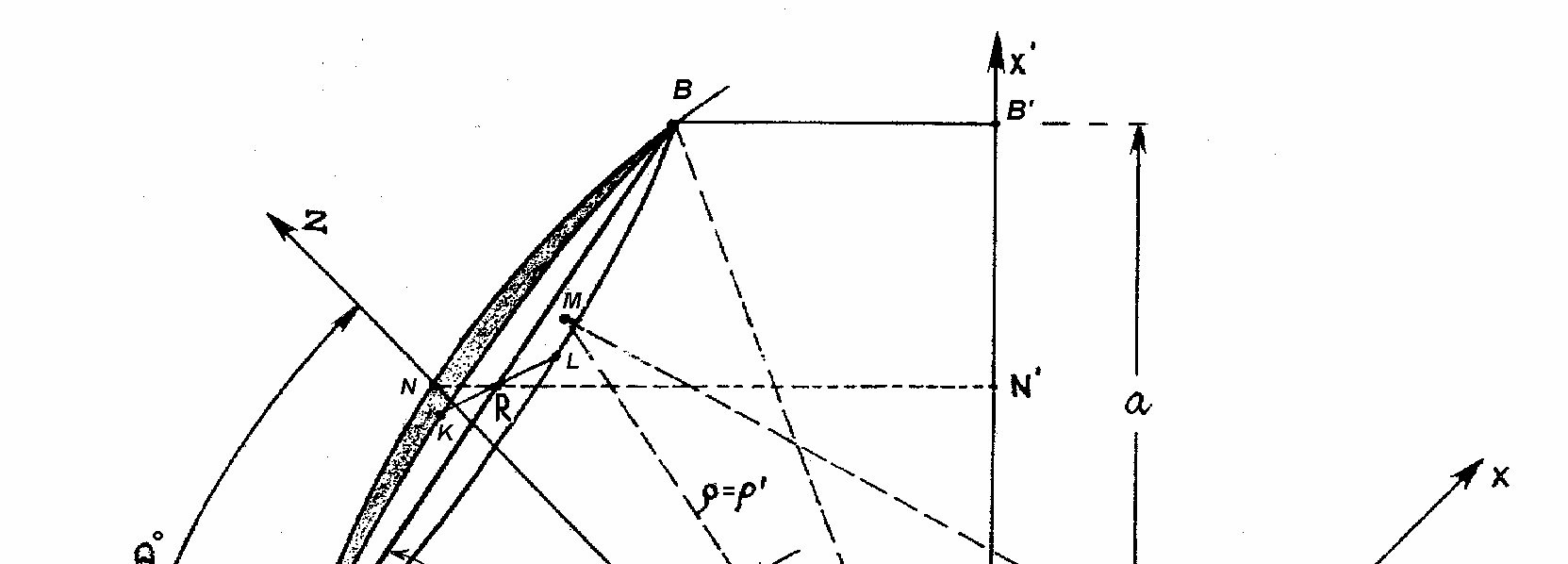
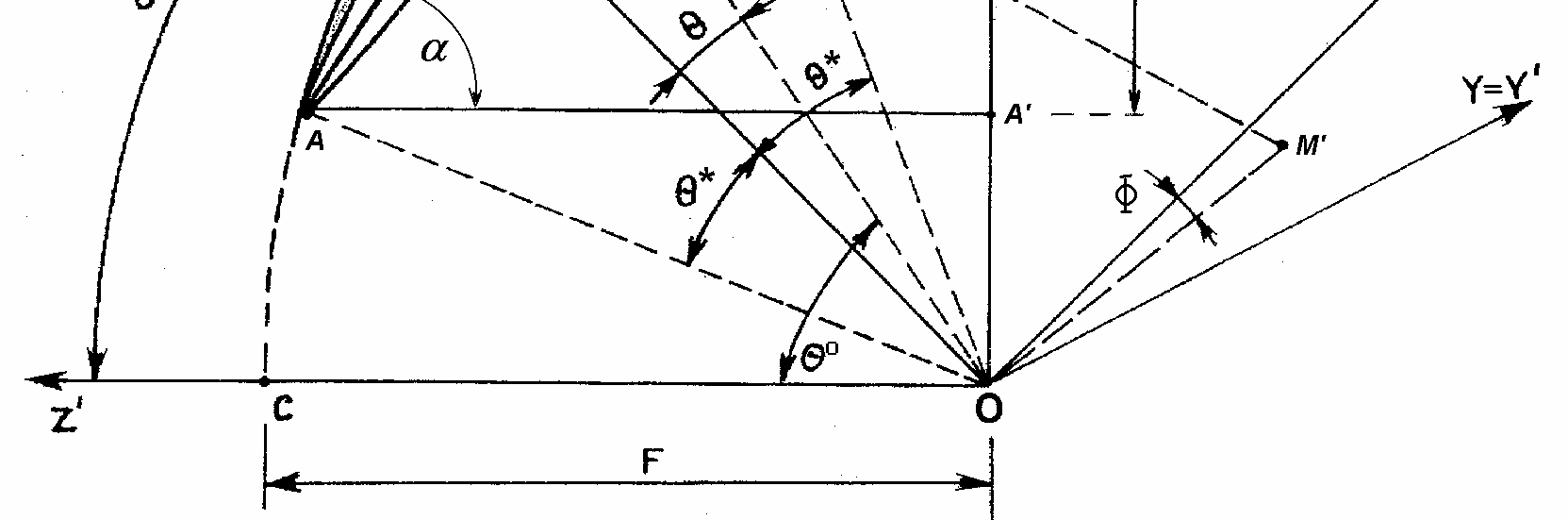
(Opis teoretyczny do ćwiczenia nr 1) Geometrię anteny zbudowanej w oparciu o reflektor będący niesymetrycznym wycinkiem paraboloidy obrotowej przedstawiono na rys. 1. Krawędź wycinka jest zdefiniowana przez przecięcie się stożka powstałego przez obrót o stały kąt Θ* wokół osi odchylonej od osi symetrii paraboloidy wyjściowej o kąt Θo. Wybór takiej geometrii reflektora wynika z przyjęcia założenia osiowej symetrii oświetlenia, co jest warunkiem podstawowym uzyskania wysokiej sprawności anteny.

Rys. 1. Geometria reflektora podś wietlanego - układy współrzę dnych.

Na rys. 1. przedstawiono zarys paraboli wyjściowej oraz wybrany fragment stanowiący reflektor w dwóch parach układów współrzędnych: (X', Y', Z') i związany z nim sferyczny układ współrzędnych (ρ’, Θ’, Φ’). Druga para układów współrzędnych powstaje przez obrót dookoła osi OY' o kąt Θo pierwszej pary układów współrzędnych.

Wzajemne transformacje układów można zapisać: Y ' = Y

X ' = X

o

cos Θ + Z

o

sin Θ

(1)

Z ' = Z

o

cos Θ − X

o

sin Θ

- 2 -

Y = Y '

X = X

o

' cos Θ + Z

o

' sin Θ

(2)

Z = Z

o

' cos Θ − X

o

' sin Θ

ρ'= ρ

cos Θ' = cos Θ cos Θ o − sin Θ sin Θ o cos Φ

(3)

sin Θ' sin Φ' = sin Θ sin Φ

sin Θ' cos Φ' = sin Θ cos Θ o cos Φ + cos Θ sin Θ o Równanie paraboloidy wyjściowej można zapisać: ρ

2 F

' =

1 + cosΘ

(4)

'

2 F

czyli

ρ'= 1+cos cos o −sin sin o

Θ

Θ

Θ

Θ cosΦ

(5)

gdzie:

F - ogniskowa paraboloidy wyjściowej.

Podstawiając do (5) równanie stożka Θ = Θ* łatwo uzyskać równanie opisujące krawędź

wycinka:

ρ =

2 F

1+

*

o

Θ

Θ −

*

o

cos

cos

sinΘ sinΘ cosΦ

(6)

Jest to równanie opisujące elipsę, której długa oś AB i krótka oś KL są zaznaczone na rys. 1.

Środek tej elipsy (punkt D na rys. 1.) nie pokrywa się z osią OZ, a jego prostokątny rzut na płaszczyznę X'Y' wyznacza środek geometryczny apertury.

Aperturę stanowi rzut reflektora na płaszczyznę prostopadłą do kierunku promieniowania, czyli w tym przypadku płaszczyznę X'Y' lub równoległą do niej. Jest to koło o średnicy :

4 F sin *

Θ

KL =

⋅ ⋅

o

cosΘ + cos *

Θ

(7)

Odległość środka apertury od początku układu współrzędnych wynosi: 2 F

o

sin Θ

ON ' =

⋅ ⋅

o

cosΘ + cos *

Θ

(8)

Z zależności (6) oraz (1) i (2) można wyznaczyć długość długiej osi elipsy: 2

o

o

* 2

sin

(cos

cos

)

AB =

*

+

+

4 F sin Θ

Θ

Θ

Θ

o

(cosΘ +

* 2

cosΘ

(9)

)

Ze wzoru (6) wynika, że elipsa ta leży na płaszczyźnie pochylonej pod kątem α do osi anteny, przy czym:

*

o

α =

cosΘ + cosΘ

arctg(

)

o

sin Θ

(10)

Rzut prostokątny reflektora na płaszczyznę prostopadłą do apertury wynosi:

*

o

sinΘ sinΘ

A' B' = 4 ⋅ F ⋅

o

(cosΘ + cos *

Θ

(11)

)2

- 3 -

Kąt offsetu rozumiany, jako kąt pomiędzy osią z’, a prostą prostopadłą do długiej osi elipsy można określić z zależności:

*

o

γ =

cosΘ

cosΘ

o − α =

o −

+

90

90

arctg(

)

o

sin Θ

(12)

Promień wolny od cieni rozumiany, jako maksymalny promień koła w płaszczyźnie ogniskowej, nie powodujący cienia geometrycznego na reflektorze: o

sin Θ

sin *

Θ

OA' = 2 ⋅

−

F

o

cosΘ + cos *

Θ

(13)

Średnica czaszy wyjściowej - minimalna średnica czaszy, z której można uzyskać żądany wycinek:

o

sin Θ

sin

*

Θ

D = 4 ⋅

+

F

o

cos Θ + cos *

Θ

(14)

oraz współczynnik kształtu tej czaszy:

F

o

*

=

cosΘ + cosΘ

(15)

D

o

4(sin Θ + sin *

Θ )

Wszystkie powyższe wielkości geometryczne wyznaczono w funkcji trzech podstawowych parametrów reflektora:

F - ogniskowej;

Θo - kąta podświetlenia

Θ* - kąta oświetlenia.

Przedstawienie reflektora anteny podświetlanej w układach współrzędnych, jak na rys. 1 jest wygodne dla analizy polowej i własności geometrycznych anteny, mało jednak czytelne, kiedy należy podać siatkę współrzędnych gotowego wycinka dla celów warsztatowych. W tej sytuacji wygodnie jest prostokątny układ współrzędnych XYZ przesunąć równolegle do punktu D -

przecięcia się długiej i krótkiej osi elipsy, a następnie obrócić wokół osi OY tak, aby oś OX

pokryła się z długą osią elipsy, jak na rys. 2.

Analityczne równanie powierzchni reflektora przyjmie wówczas postać: x 2

2

cos β + y 2 + z 2

2

sin β + 2 xz cosβ sin β + zP + K = 0

(16)

gdzie:

o

sin Θ

P = 4 ⋅ F

o

(cosΘ + cos *

Θ )sinβ

sin

*

Θ

K = −4 ⋅ F 2

2

(

)

o

cosΘ + cos *

Θ

*

o

β = Θ

cos

sin

o −

Θ

Θ

arctg(

+

)

cosΘ*

1

cosΘ o

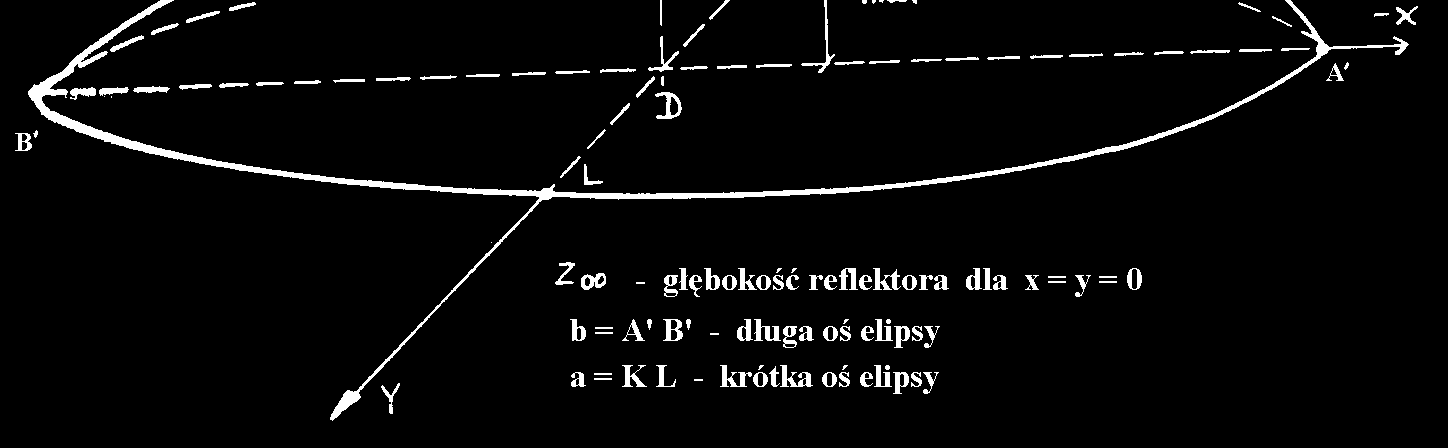
- 4 -

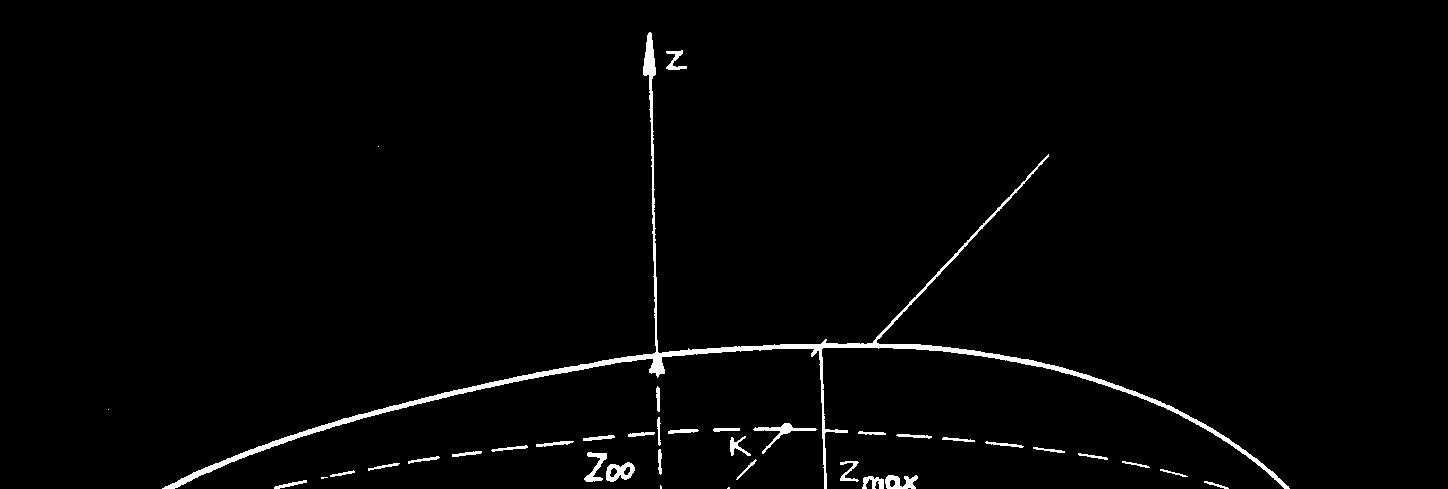
Rys. 2. Niesymetryczny wycinek paraboloidy w układzie współrzę dnych XYZ.

Wykorzystując równanie (16) można wyznaczyć podstawowe parametry geometryczne reflektora:

F

- ogniskową,

Θo

- kąt podświetlenia,

Θ*

- kąt oświetlenia,

D

- średnicę reflektora symetrycznego,

γ

- kąt offsetu,

OA

-długość wspornika,

OA’ - promień wolny od zacienienia,

Γ

- kąt nachylenia dużej osi elipsy do wspornika źródła.

Zakładając idealny kształt powierzchni reflektora (paraboloidy) przez pomiar dużej i małej osi elipsy oraz głębokości reflektora zoo (rys. 2) można wykorzystując wyżej podane zależności obliczyć podstawowe parametry geometryczne reflektora. Bardziej dokładne wyniki otrzymuje się przez pomiar kształtu paraboli wzdłuż dużej i małej osi elipsy z = f(x, y=0) i z = f(y, x=0) oraz aproksymację otrzymanych wyników. W pracach [4, 5, 6] opisane są odpowiednie programy komputerowe do obliczania podanych parametrów geometrycznych reflektora na podstawie wyników pomiarów jego geometrii (a, b, zoo lub z=f(x, y=0) i z=f(y, x=0)).